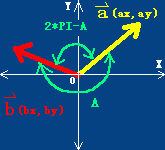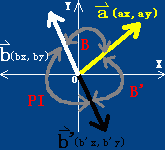向量几何在游戏编程中的使用系列三之2-D物体任意角度的反弹

2-D物体任意角度的反弹

　   这次深入充分利用向量的性质模仿一个物理现象。

　　首先，我要介绍一下将要使用的两个基本但非常重要的技巧。

　　一、求与某个向量a正交的向量b
                                                               
   根据向量内积的性质以及正交向量之间的关系，有：

　　设a=(xa，ya)，b=(xb，yb)

　　a.b = 0

　　=> xa*xb + ya*yb = 0

　　=> xa*xb = -ya*yb

　　=> xa/-ya = yb/xb

　　=> xb = -ya ， yb = xa 或 xb = ya ， yb = -xa

　　则向量(xa，ya)的正交向量为(xb，yb)=(-ya，xa)

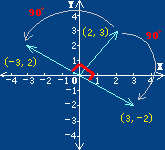
　　比如上图中，向量(2，3)的逆时针旋转90度的正交向量是(-3，2)，顺时针旋转90度的正交向量为(3，-2)。

　　这样，任给一个非零向量(x，y)，则它相对坐标轴逆时针转90度的正交向量为(-y，x)，顺时针转90度的正交向量为(y，-x)。

　　二、计算一个向量b与另一向量a共线的两个相反的投影向量

                                 

　　我们看一下上面的图，很明显，cosA(A=X)关于y轴对称，是偶函数，因此cosA = cos(-A)，

　　又因为cosA是周期函数，且周期是2*PI，则有cos(A+2*PI) = cosA = cos(-A) = cos(-A+2*PI)，

　　则根据cosA = cos(2*PI-A)以及a.b = |a|*|b|*cosA，有

　　a.b = |a|*|b|*cosA = |a|*|b|*cos(2*PI-A)

                                     

　　现在，根据上图，就有a.b = |a|*|b|*cosA = |a|*|b|*cos(2*PI-A) = ax*bx + ay*by

                                        

　　按照这个规则，当上面的b与c的模相等时，有|a|*|b| = |a|*|c|，进一步的，当它们与a的夹角A = B时，就有

　　a.b = |a|*|b|*cosA = |a|*|c|*cosB = a.c ，相应的有

　　a.b = |a|*|b|*cosA = |a|*|b|*cos(2*PI-A) = |a|*|c|*cosB = |a|*|c|*cos(2*PI-B) = a.c 也就是

　　ax*bx + ay*by = ax*cx + ay*cy

　　我们还注意到在一个周期内，比如在[0，2*PI]中，cosA有正负两种情况，分别是：在(0，PI/2)&(3*PI/2， 2*PI)为正，在(PI/2，3/2*PI)为负。好，知道了这件事情之后，再看a.b = |a|*|b|*cosA，|a|和|b|都为正，所以a.b的正负性就由cosA决定，换句话说，a.b与它们夹角A的余弦cos有相同的符号。所以，还看上面的图，我们就有：

　　1)当A在(0， PI/2)&(3*PI/2， 2*PI)中，此时2*PI-A在(-PI/2，0)&(0， PI/2)中，a.b为正

　　2)当A在(PI/2， 3*PI/2)中，此时2*PI-A也在(PI/2， 3*PI/2)中，a.b为负

                                                    

　　现在我们再来看一下同模相反(夹角为PI)向量b和b'与同一个向量a的两个内积之间有什么关系。

　　首先B + B'= 2*PI - PI = PI，所以有b = -b'， b' = -b，即

　　(bx， by) = (-b'x， -b'y) = -(b'x， b'y)

　　(b'x， b'y) = (-bx， -by) = -(bx， by)

　　所以

　　a.b =(ax， ay) . (bx， by) = (ax， ay) . -(b'x， b'y) = a.-b'= -(a.b')

　　a.b'= (ax， ay) . (b'x， b'y) = (ax， ay) . -(bx， by) = a.-b = -(a.b)

　　我们看到，一个向量b的同模相反向量b'与向量a的内积a.b'，等于b与a的内积的相反数-(a.b)。

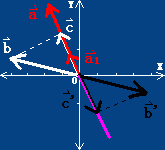
　　好，有了上面的基础，我们就可以求一个向量b与另一向量a共线的两个相反的投影向量c和c'了。

                                                                        

　　要求b在a上的投影向量c，我们可以用一个数乘上一个单位向量，这个单位向量要和a方向一至，我们记为a1.而这个数就是b在a上的投影长。

　　先来求单位向量a1，我们知道它就是向量a乘上它自身长度的倒数(数乘向量)，它的长度我们

　　可以求出，就是m = sqrt(ax^2 + ay^2)，所以a1就是(ax/m， ay/m)，记为(a1x， a1y)。

　　再求投影长/c/(注意//与||的区别，前者是投影长，可正可负也可为零，后者是实际的长度，衡为非负)。 根据内积的几何意义：一个向量b点乘另一个向量a1，等于b在a1上投影长与a1的长的乘积。那我们要求b在a上的投影长，就用它点乘a的单位向量a1就可以了，因为单位向量的长度为1，b的投影长/c/乘上1还等于投影长自身，即：

　　/c/ = b.a1 = (bx， by) . (a1x， a1y) = bx * a1x + by * a1y

　　好，我们得到了c的投影长，现在就可以求出c：

　　c = /c/*a1 = ( (bx * a1x + by * a1y)*a1x， (bx * a1x + by * a1y)*a1y )

　　总结一下，就是c = (b.a1)*a1.

　　我们看到，b与a1的夹角在(0， PI/2)之间，因此它们的点积/c/是个正值。因此当它乘a1之后，得到向量的方向就是a1的方向。

　　现在来看b'，它是b的同模相反向量，它和a1的夹角在(PI/2， 3*PI/2)之间，因此b'点乘a1之后得到/c'/是个负值，它再乘a1，得到向量的方向和a1相反。我们知道，一个向量b的同模相反向量b'与向量a的内积a.b'，等于b与a的内积的相反数-(a.b)。因此，/c'/ = -/c/，也就是说，它们的绝对值相等，符号相反。因此它们同乘一个a1，得到的的两个模相等向量c与c'共线。

　　让我们把它完成：

　　(b'.a1) = -(b.a1)

　　=> -(b'.a1) = (b.a1)， 好，代入c = (b.a1)*a1，得到

　　c = -(b'.a1)*a1

　　=> (b'.a1)*a1 = -c = c'

　　c = ( b . a1 ) * a1 = (-b'. a1) * a1

　　c'= ( b'. a1 ) * a1 = (-b . a1) * a1

　　至此为止，我们得出结论：当一个向量b与另一个向量a的夹角在(0， PI/2)&(3*PI/2， 2*PI)之间，它在a方向上的投影向量c就是c = ( b . a1 ) * a1，其中a1是a的单位向量；它在a相反方向的投影向量c'是c'= ( b'. a1 ) * a1，其中向量b'是b的同模相反向量。