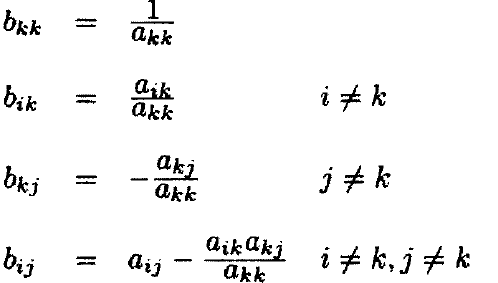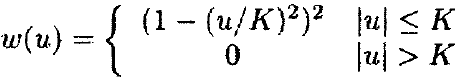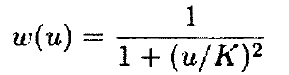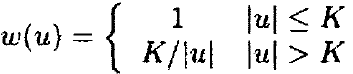Lisp-Stat翻译 —— 第五章 统计函数
第五章 统计函数
Lisp-Stat里的一些统计函数已经在前几章里介绍了。这些函数的多数都是处理数值数据集的,表示为Lisp-Stat组合数据项。本章的第一节将介绍一些额外的函数用来检测复合数据和矢量运算系统。接下来的一节描述了用来处理数据、相关标准概率分布的计算和数值线性代数计算的一些函数。这些函数中的很多模仿了S系统里的相似的函数。本章以两个列子作为结束,这两个例子说明了一些介绍过的工具的用法。
5.1 组合数据
5.1.1 组合数据属性
组合数据包括列表、矢量、数组合组合数据对象(这个下一章介绍)。非组合数据叫做简单数据。谓词compound-data-p可以用来确认组合数据项。
组合数据项的主要特征是它们包含数据项的序列。这个序列可以使用函数compound-data-seq来提取。对于列表和矢量该函数仅返回它的参数。对于数组它返回一个元素为行主序的替换数组。复合数据项的元素本身也可以是组合的。函数element-seq递归地遍历组合数据项并且返回它的简单元素序列:
> (compound-data-seq '(a (b c))) (A (B C)) > (element-seq '(a (b c))) (A B C)如果一个组合数据项的所有元素都是简单数据,那么element-seq函数与compound-data-seq函数的效果是等价的。
函数count-elements返回简单项的数量,即element-seq函数的结果的长度:
> (count-elements '(a (b c))) 3
5.1.2 矢量化计算
在前几章中,我们已经简略点讨论了矢量化计算的几个要点。本小节讨论一些与这个主题相关的问题和惯例。
大多数统计操作都涉及到对数值集合的操作。为了简化函数编写来表现这些操作,Lisp-Sstat重定义了基本Lisp计算函数+、-、*、/、log等等,目的是将组合数据作为参数,并且返回组合数据项,这些数据项是通过将这些函数作用到组合数据的每一个元素上得到的。
Lisp提供了一些映射函数来将函数逐元素地作用到列表项或者矢量项上。因为两个原因,这些函数不能直接用来实现矢量运算。首先,在表达式(+ '(1 2 3) 4)里,它的意图是将4加到列表(1 2 3)的每一个元素上。因为参数4不是一个列表,一些像mapcar一样的函数就不能直接作用在它们上边。我们想要一个常量被看成就像是一个常量列表或者合适长度或维度的数组,而不需要一定要强制构建它。
对于第二个原因,考虑到以下表达式(+ '(1 2 3) '#(4 5 6)),它的意图就是逐元素地对两个序列相加,然后返回结果。但是,一个序列是列表,而另一个是矢量。那本例中的结果会是什么呢?map函数需要结果序列的类型必须强制指定。因为这个可能不太方便,在参数类型不同时,我们需要使用一个约定来确定结果的类型。Lisp-Stat里使用的约定就是从参数列表的第一个组合数据项里提取任何需要的结构信息,包括类型、长度、维度等等。其它组合数据参数必须匹配第一个组合数据参数的形式。多个序列,如果它们之间长度相同,无论类型是否相同,都被视为是有相同形式的。多维数组之间,如果它们的维度是相同的,那它们就是有相同形式的。
用来处理常量和确定结果结构的这些规则在函数map-elements的定义中用到过,那个函数是在3.7节介绍的。
在实现矢量化计算函数的过程里,还需要做一个决定:像(+ '(1 (2 3)) 4)这样的表达式如何被求值?有两个选择,如果我们仅允许一个层级的矢量化计算的话,那么这个表达式将导致一个错误。换句话说,我们可以递归地矢量化加法函数,为表达式产生(5 (6 7))这样的结果。哪一个选择是正确的不太清晰,我是决定使用递归矢量化的。
5.2 数据处理函数
5.2.1 基础操作
用来产生成系统的数据的函数,如repeat、iseq和rseq,已经在第二章里介绍过了。和它们相关的还有函数difference,它作用于数字序列,返回相邻两个元素之间的差分:
> (difference '(1 3 6 10)) (2 3 4) > (difference #(1 3 6 10)) #(2 3 4)函数split-list带一个列表和一个整数长度n,然后将列表分裂成列表的列表,每个子列表长度为n:
> (split-list '(1 2 3 4 5 6) 3) ((1 2 3) (4 5 6))如果列表的长度不是n的倍数,将发送一个错误信号。
函数cumsum带有一个序列作为参数,然后返回原序列的累计和序列:
> (cumsum '(1 2 3 4)) (1 3 6 10) > (cumsum #(1 2 3 4)) #(1 3 6 10)
累积和也可以使用accumulate函数来计算,这个函数带有一个二进制函数和一个序列为参数,然后返回一个新的结果序列,这个新序列是将二进制函数累积地作用到原序列的每一个元素后得到的结果。那么累加可以这样计算:
> (accumulate #'+ '(1 2 3 4)) (1 3 6 10)累积则产生:
> (accumulate #'* '(1 2 3 4)) (1 2 6 24)一些函数对组合数据项计算简单总结。除了在第二章介绍的函数mean和standard-deviation,这样的函数还包括count-elements、sum、prod、max和min。这些函数叫做矢量减少函数,因为它们减少组合数据项成为单个数字。
函数min和max可以带多个参数,但是它们通常返回所有参数的最大值和最小值。函数pmin和pmax是矢量化的函数,可以用来并行地计算多个参数的最大值与最小值。例如:
> (pmin '(1 2 3 4 5) '(5 4 3 2 1)) (1 2 3 2 1)最后,函数covariance-matrix带序列或者矩阵为参数,并将它们形成一个列的列表形式,然后对这个数据列返回样本的协方差矩阵。所有的数据列都应该是等长度的。
5.2.2 排序函数
函数sort-data带一个组合数据项参数,返回一个排好序的元素的序列。元素应该都是实数或者字符串。字符串排序是大小写敏感的。
order函数将element-seq函数作用到参数上,返回一个最小的和第二小的下标的列表。元素序列的元素。rank函数带一个组合数据项作为参数,返回一个相同大小的组合数据项,该数据的条目被它的阶数代替:
> (rank '(14 10 12 11)) (3 0 2 1) > (rank '#2a((14 10) (12 11))) #2A((3 0) (2 1))最低的阶是0,联系被任意打断。(注:此处不甚了解,可能翻译不精确!!!)
函数quantile带两个参数,分别是一个组合数据项x和一个数字或数字序列p,0≤p≤1,然后返回x的第p级分位数:
> (def x (uniform-rand 20)) X > (quantile x .5) 0.6490398497045595 > (quantile x '(.2 .8)) (0.44269173085226765 0.8681219493754327)函数median、interquartile-range和fivnum是使用术语quantile定义的。fivum返回参数的最小值、第一分位数、第二分位数、第三分位数和最大值,即五数概括法。
5.2.3 插值和平滑
函数spline带连个等长度的序列x和y作为参数,然后针对这两个序列里指定的点返回一个自然三次样条插值的x与y值的列表。参数x里的值必须严格递增。默认情况下,插值函数将在x值的范围内计算30个等距离点。这个可以通过使用关键字:xvals来改变。如果使用了这个关键字,其值为整数n的话,那么结果会使用n个等距离点来代替30等距离点。因此表达式
(let ((x (rseq 0 pi 10)))
(spline x (sin x) :xvals 50)) 将使用50个点返回正弦函数的插值。如果使用了:xvals关键字,其值为一个序列的话,那么这个序列将被用作计算样条时的那个x值。所以我们的50点插值也可以这么构建:
(let ((x (rseq 0 pi 10)))
(spline x (sin x) :xvals (rseq 0 pi 50))) lowess函数使用LOWESS平滑算法作用到两个序列值x和y上。它返回x序列的列表和y序列的平滑值。所以表达式
(setf p (plot-points x y)) (setf p :add-lines (lowess x y))将使用变量x和y的数据构建一个散点图,然后使用LOWESS算法对图形进行平滑处理。
LOWESS算法的一些参数可以通过向lowess函数船体关键字参数来控制。用来估计每个点的拟合程度的数据的分数通过关键字:f来指定;默认值为0.25。稳定迭代的数量可以使用关键字:steps来指定,默认值为2。最后,在给定点处的拟合使用线性插值确定的。这个临界值可以使用关键字:delta来改变,默认值为x值的范围的2%。
函数kernel-smooth提供了一个备用的平滑函数。它以x和y序列为参数,返回x值的列表和平滑后的y值的列表的集合。默认地,结果的x值是在输入的x值的范围上的30份的等距离点。针对spline函数,关键字:xvals可以用来指定点数量的备选值,或者是针对结果的x值的序列的备选值。核心的4个类型都是被支持的,指定符号G代表高斯,指定符号T代表三角形,指定符号U代表正态,指定符号B代表二项分布。默认核是二项分布,但是你可以使用关键字:type来指定备用的核。核的宽度可以使用关键字:keyword来指定。因此表达式
(send p :add-lines (kernel-smooth x y :type 'g))将向上边的绘图结构里加入一个高斯核平滑。
核密度估计量也是可用的。kernel-dens需要一个单独的x值的序列作为参数,返回x值的列表和密度估计值。表达式
> (plot-lines (kernel-dens (normal-rand 50))) #<Object: 1431e04, prototype = SCATTERPLOT-PROTO>针对50标准正态随机变量组成的样本,产生一个核密度预测的图形。kernel-dens函数接受与kernel-smooth函数相同的关键字参数。
5.3 概率分布
Lisp-Stat含有一些函数,用来评估一些连续单变量分布的密度、累积分布函数和分位数,包括正态分布、柯西分布、β-分布、γ-分布、x²-分布、t-分布和F-分布。
用来计算二项式分布和泊松分布的概率密度函数、累积密度函数和分位数函数的类似函数是可用的。针对这些离散分布的quantile函数被定义成如下形式:累积分布函数的左连续逆。概率密度函数仅被定义为整型参数。最后,还有一个用来估计二元正态分布的累积分布函数的估值的函数,这些可用的函数见下表,所有的函数都是矢量化的:
针对正态分布和柯西分布的函数假设是标准分布,因此只需要一个参数,这里的值未来计算密度函数或者累积分布函数,这里的0和1之间的比例系数,用来估计分位数函数。针对γ-分布、x²-分布、t-分布和泊松分布的函数还需要一个额外的参数:分别是γ指数、x²和t分布的自由度,还有泊松均值。假定γ-分布有一个尺度为1的参数。这有几个例子:
> (chisq-cdf 7.5 8) 0.5162326184463124 > (t-quant .975 3) 3.1824463052837086 > (poisson-pmf 3 2.5) 0.2137630172497364针对β-分布、F-分布和二项式分布的函数需要两个额外的参数:分别是β-分布的两个指数、F-分布的分子和分母的自由度,二项式分布的样本大小与成功的可能性。针对这个也有几个例子:
> (beta-cdf .3 5.2 6.3) 0.14839195210538714 > (f-quant .9 3 7) 3.0740719939090018 > (binomial-pmf 3 5 .5) 0.3124999999999998函数bivnorm-cdf假设两个边际都是标准正态的,它带三个参数,累积分布函数需要的x和y参数,还有相关性系数:
> (bivnorm-cdf .3 .2 .6) 0.4551159427475644在第2.4.1节里描述的这些分布的随机数字生成器是使用Common Lisp随机数生成器实现的。Common Lisp随机数接口是打算要跨不同系统的。我们使用的特定的生成器可能随着我们使用系统的不同产生不同的数值。生成器的种子通常使用系统时钟生成,可以保存和恢复,也可以生成新的种子。但是却不能为生成器指定一个任意种子,因为一个适当的选择是依据生成器的实现、机器的字长等等因素的。
状态的当前值保存在全局变量*random-state*里。函数make-random-state可用来设置和保存状态。该函数带有一个可选参数,吐过这个参数是nil或者被忽略的话,那么make-random-state函数将返回变量*random-state*的当前值的一份拷贝。如果参数是一个随机状态对象,将返回它的拷贝。最后,如果参数是符号t的话,将产生一个新的随机化的初始化状态对象然后返回它。通常使用系统时钟产生新的种子,但是精确的机制是随之Lisp系统的不同而不同的。
一个带打印表达式的随机状态对象可以使用read函数读回。因此你可以将当前状态保存到一个文件里,然后使用它重复一个带有伪随机数的相同流的模拟过程。例如,使用表达式将当前状态写入到文件之后:
(with-open-file (s "currentstate" :direction :output)
(print *random-state* s)) 以下表达式
(with-open-file (s "currentstate")
(setf *random-state* (read s))
(run-simulation))
每求值一次,都会使用相同的随机数字集合来重复模拟器。
5.4 数组和线性代数函数
5.4.1 基本矩阵和数组函数
矩阵是二维数组,在统计计算中扮演一个重要的角色,所以Lisp-Stat提供了一些附加函数来帮助管理矩阵。谓词matrixp遇到一个矩阵时返回t,遇到其它类型数据将返回nil。
有时候,能够将列表或者矢量集合拼接到成矩阵的行或列是很有用的。可以使用函数bind-rows和bind-columns:
> (bind-rows '#(1 2 3) '(4 5 6)) #2A((1 2 3) (4 5 6)) > (bind-columns '#(1 2 3) '(4 5 6)) #2A((1 4) (2 5) (3 6))传递给bind-rows和bind-columns函数的参数可能是矩阵:
> (bind-rows '#2a((1 2 3) (4 5 6)) '(7 8 9)) #2A((1 2 3) (4 5 6) (7 8 9))这个可以被利用来编写一个函数,该函数使用两个矢量和一个常量形成矩阵的新边界:
> (defun border-matrix (a b c d)
(bind-rows (bind-columns a b)
(concatenate 'list c (list d))))
BORDER-MATRIX 然后,举个例子:
> (border-matrix '#2a((1 2) (3 4)) '(5 6) '(7 8) 9) #2A((1 2 5) (3 4 6) (7 8 9))例如,为了能够计算列的平均值,你需要将矩阵拆散成列。column-list函数就是执行这个惭怍的:
> (column-list '#2a((1 2 3) (4 5 6))) (#(1 4) #(2 5) #(3 6))现在,可以使用mapcar函数定义column-mean函数了:
> (defun column-means (x)
(mapcar #'mean (column-list x)))
COLUMN-MEANS
还有四个函数也值得一提。transpose函数带一个矩阵作为参数,返回参数的转置。transpose函数也可以用来表示具有相同长度的列表集的列表的转置,表示矩阵的行。然后它返回列表集的列表,代表转置的行。函数identity-matrix带一个整型参数k,返回一个k乘k的特征矩阵。函数diagonal有两种用法。传递给它一个矩阵作为参数,它返回矩阵对角线项的列表(这个矩阵必须是方阵):
> (diagonal '#2a((1 2) (3 4))) (1 4)如果传递给它一个序列参数,diagonal返回一个方阵,该方阵的对角线上的元素就是序列的元素,其它元素为0。
> (diagonal '(a b c)) #2A((A 0 0) (0 B 0) (0 0 C))最后,print-matrix函数可以用来打印一个比传统打印机方法更好的矩阵表达式:
> (print-matrix #2a((1 2 3) (4 5 6) (7 8 9)))
#2a(
(1 2 3 )
(4 5 6 )
(7 8 9 )
)
NIL 与print函数类似,函数print-matrix也接受可选参数。
Lisp-Stat还提供了一个函数permute-array,它带一个数组和一个列表作为参数,然后根据列表指定的转置对数组进行转置:
> (permute-array '#2a((1 2 3) (4 5 6)) '(1 0))
#2A((1 4) (2 5) (3 6))
> (permute-array '#3a(((1 2 3) (4 5 6)) ((7 8 9) (10 11 12)))
'(2 0 1))
#3A(((1 4) (7 10)) ((2 5) (8 11)) ((3 6) (9 12)))
5.4.2 矩阵乘法
函数带两个矩阵为参数,并对它们运行乘法操作。矩阵的元素必须是数字。
> (matmult '#2a((1 2 3) (4 5 6)) '#2a((1 2) (3 4) (5 6))) #2A((22.0 28.0) (49.0 64.0))
参数中的一个也可以是一个序列——一个列表或者一个矢量。若果是这种情况,并且它是第一个参数的话,这个序列被当成一个行矢量;如果它是第二个参数的话,它将被当成列矢量。结果是与序列参数是相同类型的一个序列:
> (matmult '#(1 2) '#2a((1 2 3) (4 5 6))) #(9.0 12.0 15.0) > (matmult '#2a((1 2 3) (4 5 6)) '(1 2 3)) (14.0 32.0)如果传递给函数matmult的参数都是具有相同长度的序列,将返回一个数值,也就是两个参数的内积。内积也可以使用inner-product函数来计算求得:
> (matmult '(1 2 3) '#(4 5 6)) 32.0 > (inner-product '(1 2 3) '#(4 5 6)) 32.0matmult函数可以通过传递多于两个参数来调用。在这种情况下,前两个参数相乘,其结果再与右边的第三个参数相乘,等等。
函数outer-product函数带两个序列作为参数,返回他们的外积:
> (outer-product '#(1 2) '(3 4 5)) #2A((3 4 5) (6 8 10))outer-product提供了一个一般意义上的外积。它有一个可选参数,该可选参数是一个带两个参数的函数。如果outer-product函数使用了这个可选参数,那么它的结果的(i, j)位置的元素是这样的两个数的乘积组成的:第一个序列的第i个元素和第二个序列的第j个元素:
> (outer-product '#(1 2) '(3 4 5) #'+) #2A((4 5 6) (5 6 7))函数cross-product带一个参数x,返回(matmult (transpose x) x)的值。
5.4.3 线性代数函数
Lisp-Stat提供了一些进行线性代数运算的函数。其中一个经常会被其它函数调用的函数就是lu-decomp函数。该函数带一个数值方阵,然后运行带局部定支点的LU分解,最后返回4个元素的列表。第一个元素是一个包含LU分解的方阵,该方阵定支点过程确定的那个矩阵的以行为主的排列的LU分解方阵。除对角线外,下三角矩阵是L部分;L的对角线元素全为1。结果矩阵的上三角部分,包括对角线,是U部分。结果列表的第二个元素是一个整数的矢量,用来描述定支点过程里用到的排列。第三个元素是一个数字,它等于±1,如果用来进行航互换的数目为偶数,它就是正1,;是技术的话,该参数就取负1。结果矩阵的最后一个元素是一个标志,如果输入矩阵是数值上的奇异矩阵,该值为t;如果是非奇异矩阵,该值为nil。
> (lu-decomp '#2a((1 2) (3 4))) (#2A((3.0 4.0) (-0.3333333333333333 0.6666666666666667)) #(1 1) -1.0 NIL)lu-solve函数带两个参数。第一个参数是由函数lu-decomp使用矩阵A返回的结果。第二个参数是一个列表或者矢量,它是表达式Ax = b的右值b。lu-solve函数使用带LU分解功能的back-solving解法解该方程,然后返回结果。
> (lu-solve (lu-decomp '#2a((1 2) (3 4))) '(5 6)) (-3.9999999999999987 4.499999999999999) > (matmult '#2a((1 2) (3 4)) '(-4 4.5)) (5.0 6.0)在back-solving算法处理期间,如果矩阵被发现是数值上奇异的,将发生一个错误信号。
determinant、inverse和solve这几个函数将使用LU分解来处理它们的矩阵参数。determinant函数带有一个矩阵作为参数,然后返回它的行列式。inverse返回参数矩阵的逆矩阵,如果这个矩阵是数值奇异的则发送一个错误信号。
> (inverse '#2a((1 2) (3 4))) #2A((-1.9999999999999996 0.9999999999999998) (1.4999999999999998 -0.4999999999999999)) > (matmult '#2a((1 2) (3 4)) '#2a((-2 1) (1.5 -0.5))) #2A((1.0 0.0) (0.0 1.0))solve函数带有一个矩阵A和一个参数b作为参数,然后返回Ax = b的解。b可以是一个序列或者一个矩阵。
> (solve '#2a((1 2) (3 4)) '(5 6)) (-3.9999999999999987 4.499999999999999) > (solve '#2a((1 2) (3 4)) (identity-matrix 2)) #2A((-1.9999999999999998 0.9999999999999999) (1.4999999999999998 -0.4999999999999999))lu-decomp、lu-solve、determinant、inverse和solve等函数的参数可以包含实数或者复数。
chol-decomp函数带有一个对称方阵A作为参数,然后计算矩阵A+D的cholesky分解,这里的D是一个非负的对角矩阵,它被加到A矩阵上,如果能确保A+D是数值上严格正值定义。由函数chol-decomp返回的结果是下三角矩阵L的一个列表,矩阵L满足LLT= A+D,该返回值是D的元素里的最大值。如果矩阵A是严格的正值定义,结果的第二个元素为0:
> (setf x (chol-decomp '#2a((2 1) (1 2)))) (#2A((1.4142135623730951 0.0) (0.7071067811865475 1.224744871391589)) 0.0) > (matmult (first x) (transpose (first x))) #2A((2.0000000000000004 1.0) (1.0 1.9999999999999996))qr-decomp带一个m行n列的矩阵A作为参数,这里m≥n,然后计算其QR分解,返回的结果是一个列表,该列表是由两部分组成的:一个带正交列的m行n列矩阵Q,一个上三角矩阵R,比如说QR = A:
> (setf x (qr-decomp '#2a((1 2) (3 4) (5 6)))) (#2A((-0.16903085094570325 0.8970852271450608) (-0.50709255283711 0.2760262237369412) (-0.8451542547285165 -0.34503277967117696)) #2A((-5.916079783099616 -7.4373574416109465) (0.0 0.8280786712108248))) > (matmult (first x) (second x)) #2A((0.9999999999999997 1.9999999999999996) (3.0 4.0) (4.999999999999999 6.0))我们可以使用print-matrix函数来使结果更有可读性:
> (print-matrix (first x))
#2a(
(-0.169031 0.897085 )
(-0.507093 0.276026 )
(-0.845154 -0.345033 )
)
NIL
> (print-matrix (second x))
#2a(
( -5.91608 -7.43736 )
( 0.000000 0.828079 )
)
NIL 如果函数qr-decomp使用了值为t的:pivot关键字,它将重新排列矩阵的列以确保矩阵R的对角线元素的绝对值是没有增长的。在这种情况下,返回的结果里将包含第三个元素,也就是按它们被使用的顺序的那些列的下标号。
sv-decomp函数带有一个m行n列的矩阵A作为参数,这里的m≥n,然后计算它的奇异值分解。该函数返回(U W V FLAG)形式的列表,这里的U和V都是矩阵,它们的列是左奇异和右奇异矢量,W是递减序列上的矩阵A的奇异值矢量。FLAG在算法收敛的时候,值为t,否则值为nil。如果FLAG是t,并且矩阵D是一个W为对角线元素,其它位置为0的一个对角线矩阵的话,那么UDVT= A:
> (setf x (sv-decomp '#2a((1 2) (3 4) (5 6))))
(#2A((-0.22984769640007144 0.8834610176985256) (-0.5247448187602937 0.2407824921325462) (-0.8196419411205158 -0.4018960334334318)) #(9.525518091565107 0.5143005806586441) #2A((-0.6196294838293404 -0.7848944532670524) (-0.7848944532670524 0.6196294838293404)) T)
> (matmult (first x)
(diagonal (second x))
(transpose (third x)))
#2A((0.9999999999999994 1.9999999999999993) (3.0 3.9999999999999996) (4.999999999999999 6.0)) 函数eigenvalues
以递减的顺序
返回一个特征值的向量;函数eigenvectors返回一个对应于一个对称方阵的特征向量的列表。eigen函数返回一个列表,它的两个元素是:一个特征值的向量,一个对称方阵的特征向量的列表。函数backsolve带有一个上三角矩阵A和一个序列b为参数,返回Ax = b的解。函数rcondest返回一个上三角矩阵的条件数的倒数的估计值。(注:矩阵的条件数就是
一个矩阵的最大奇异值与其最小奇异值之比。)
最后一个函数在构造某些动态图形时是非常有用的,它就是make-rotation函数。这个函数带有两个等长度的序列和一个可选的实数作为参数,该实数表示一个角的弧度数。它返回旋转矩阵,该旋转矩阵在由两个序列定义的平面里旋转而成,并保持从第一个序列到第二个序列的正交补不变。例如:
> (make-rotation '(1 0 0 0) '(1 1 1 1) (/ pi 10)) #2A((0.9510565162951535 -0.17841104488654497 -0.17841104488654497 -0.17841104488654497) (0.17841104488654497 0.9836855054317178 -0.01631449456828216 -0.01631449456828216) (0.17841104488654497 -0.01631449456828216 0.9836855054317178 -0.01631449456828216) (0.17841104488654497 -0.01631449456828216 -0.01631449456828216 0.9836855054317178))以上表达式返回一个矩阵,该矩阵在第一个坐标轴和一个四维空间的对角线的平面里以π/10的角度旋转。如果make-rotation函数没有给定角度参数,它将使用两个序列中较小的角度。
Lisp-Stat内部的线性代数函数使用double-float或者long-float类型的浮点数,使用哪个依赖Lisp系统和硬件。全局变量machine-epsilon合适类型的最小的浮点数x,因此,表达式(not (= 1 (+ 1 x)))将返回false,即:
> (setf x machine-epsilon) 1.0842021724855044E-19 > (not (= 1 (+ 1 x))) NIL
5.5 回归计算函数
回归计算可以使用文献65里的问题2.7提到的消除操作来执行。消除是按行执行的。也就是说,在中心点k上清除一个矩阵A就是使用给定的元素将它转换为矩阵B:
清除操作的定义是累积的、自反相的:两个中心点被清除的地方,它们的位置是无关紧要的,在同一点上进行两次清除操作与在该中心点没有进行清除操作是等价的。(注:该段理解不清,翻译可能不准确,后期研究清除再补上!)
函数mak-sweep-matrix带一个矩阵x、一个序列y和一个可选的权重的序列w,返回校正的叉积矩阵,该叉积矩阵已经在常量行上被消除掉了。也就是说,如果A是由一个只有1的列,一个x的多列和列y组成的。矩阵W是一个对角线矩阵,该矩阵列对角线上的元素就是w。那么,make-sweep-matrix函数计算叉积矩阵ATWA,然后在常数行上消除它。
函数sweep-operator带一个矩阵,一个要消除的行坐标的序列和一个可选的容插值序列作为参数,它返回一个列表,该列表由在指定行消除的矩阵的一份复制和事实上要消除的行的下标的列表组成的。仅当中心点的绝对值比指定的误差容差值大的时候才消除,默认容差值是0.000001。
如果一个叉积矩阵已经在一个中心点集合上被消除,那么被消除的矩阵的最下边一行的对应元素将是由消除的中心点索引的变量组成的那个模型的最小二乘系数。那么一个带x矩阵但排除其常数项,一个y向量和一个权值矩阵序列为参数,并且用来计算最小二乘系数的函数可以这样定义:
> (defun reg-coefs (x y weights)
(flet ((as-list (x) (coerce (compound-data-seq x) 'list)))
(let* ((m (make-sweep-matrix x y weights))
(p (array-dimension x 1)))
(as-list (select (first (sweep-operator m (iseq 1 p)))
(+ p 1)
(iseq 0 p))))))
REG-COEFS select表达式返回的结果是一个1行p+1列的矩阵,首先使用函数compound-data-seq将该矩阵转换为一个矢量,然后使用函数coerce转化为一个列表。该定义假设模型包含一个截距。对于没有截距的模型,我们需要首先消除下标0来移除常数项,仅仅选择下标为1, 2, 3, ...,p的项作为结果。
5.6 一些例子
本节将给出两个额外的例子,它们使用是使用本章里介绍的一些工具完成的。第一个例子是我们早前使用的make-projection函数的稍微显得更加详尽的版本;第二个例子是一个函数,该函数的用途是针对大量的权值函数计算其稳定的回归系数。
5.6.1 构造一个投影操作符
在第三章里我们看到了一些关于函数的变量,它们使用一个函数闭包建立了一个投影操作符的模型。那时我们仅能较容易地处理一维空间上的投影,但是现在我们拥有一些可以处理高维投影的工具,一个方法使用列表的列表或者向量的方式生成一个空间,使用它们作为矩阵X的列,然后形成X的特征值分解矩阵UDVT。矩阵U的列对应正特征值,然后形成一个关于X的列空间的正交基。因此如果U1 是这些列的矩阵,那么向量y在X列空间上的投影Py可以这样表示:Py = U1U1Ty 。
在make-projection函数的新版本的定义里,如果需要,我们通过使用表达式(if (matrixp cols) cols (apply #'bind-columns cols)),允许指定的列以向量的列表或者一个矩阵的形式转换成一个矩阵。
在使用u计算矩阵U,并且使用s-vals来计算特征值之后,我们可以这样计算非零特征值的列集列表:(select (column-list u) (which (> s-vals 0.0)))。这些列可以通过使用bind-columns函数形成矩阵U1。
在最终的投影计算里,我们可以避免在U1的左侧乘一个列表或者向量y来对U1进行转置,我们可以使用结果,该结果也可能是一个列表或者向量,将它放到U1的右侧,就像下边的表达式:(matmult u1 (matmult y u1))。
合并这些步骤,我们得到以下定义:
> (defun make-projection (cols)
(let* ((x (if (matrixp cols)
cols
(apply #'bind-columns cols)))
(svd (sv-decomp x))
(u (first svd))
(s-vals (second svd))
(basis (select (column-list u)
(which (> s-vals 0.0))))
(u1 (apply #'bind-columns basis)))
#'(lambda (y) (matmult u1 (matmult y u1)))))
MAKE-PROJECTION 练习 5.1
略。
5.6.2 稳健回归
对一个形如y = Xβ的线性模型,计算其稳健回归的方法是使用一个可以交互地重定义权值的最小二乘算法,该算法里的权值是使用一个文件的权值函数w计算的,该权值矩阵对有较大标准化残差的观测值赋予较小的权重。特别地,给定一个权重的集合,我们可以:
- 计算带权值的最小二乘估计量β帽(上边带一个尖帽,表示β的估计量)
- 计算残差r
- 计算一个范围的估计量s帽(上边带一个尖帽,表示s的估计量),作为被0.6745划分的中位数绝对残差
- 计算权值的一个新的集合,w(r/(s帽))
然后这些步骤将重复运行,直到满足收敛准则。范围估计量包括除以0.6745,以确保它是对正态分布数据的做出的全局标准差估计。
在文献中,有很多不同的权值函数被提出,包括biwieight函数:
柯西权值函数:
还有Huber权值函数:
这三个参数都依赖一个调整参数K。对于biweight函数,K的建议值是4.685;对于柯西权值函数,K的建议值是2.385;对于Huber权值函数,K的建议值是1.345。
在实现一个稳健回归函数过程中,假设模型里包含一个截距,还有一个在指定的X矩阵里的列集,我们从这里开始。对于给定的权值集合,带权值的最小二乘估计可以像使用函数reg-coefs函数一样计算,该函数是在5.5节里定义的。如果我们获得了参数集合,记做bate列表,我们就可以这样计算它的拟合值:
(+ (first beta) (matmult x (rest beta)))。
可以使用一个do循环来控制迭代,就像这样:
(do ((lase nil beta)
(count 0 (+ count 1))
(beta (reg-coefs weights) (improve-guess beta)))
((good-enough-p last beta count) beta)) 迭代变量last用来处理系数集的前一个值,目的是与当前的猜测值作比较;nil的初始值用来说明没有可用的前一个值了。迭代的总次数也被监测。
如果变量wf引用了权值函数,那么improve-guess函数的函数体可以这样编写:
(let* ((resids (- y (fitvals beta)))
(scale (/ (median (abs resids)) 0.6745))
(wts (funcall wf (/ resids scale))))
(reg-coefs wts)) 最后,如果迭代次数超出给定范围,good-enough-p函数应该打印一条消息,并且检查参数估计量的改变是否足够的小。可以这样编写测试表达式:
(flet ((rel-err (x y) (mean (/ (abs (- x y)) (+ 1 (abs x))))))
(or (> count count-limit)
(and last (< (rel-err beta last) tol))))
这里的and表达式首先检查last变量是否为nil,然后用参数列表里的平均相对变化与容差值tol的比较。在改变计算时加1是要保证对大的系数以相对误差量度,对小的系数以绝对误差量度。其它的选择是明显可能的。
现在我们可以将这些元素组合到一个单一函数里,使用一个labels表达式来定义一些函数用以实现每一步。使用关键字参数指定初始权重、收敛法则的容差值和迭代次数的边界值:
> (defun robust-coefs (xy wf &key
(weights (repeat 1 (length y)))
(tol 0.0001)
(count-limit 20))
(let ((x (if (matrixp x) x (apply #'bind-columns x))))
(labels ((as-list (x) (coerce (compound-data-seq x) 'list))
(rel-err (x y)
(mean (/ (abs (- x y)) (+ 1 (abs x)))))
(reg-coefs (weights)
(let* ((m (make-sweep-matrix x y weights))
(p (array-dimension x 1)))
(as-list
(select (first (sweep-operator m (iseq 1 p)))
(1+ p)
(iseq 0 p)))))
(firstvals (beta)
(+ (first beta) (matmult x (rest beta))))
(improve-guess (beeta)
(let* ((resids (- y (fitvals beta)))
(scale (/ (median (abs resids)) 0.6745))
(wts (funcall wf (/ resids scale))))
(reg-coefs wts)))
(good-enough-p (last beta count)
(if (> count count-limit)
(format t "Iteration limit exceeded~%"))
(or (> count count-limit)
(and last (< (rel-err beta last) tol)))))
(do ((last nil beta)
(count 0 (+ count 1))
(beta (reg-coefs weights) (improve-guess beta)))
((good-enough-p last beta count) beta)))))
ROBUST-COEFS 为了使用该函数,你需要指定一个权值函数。为了容易地使用上边列出的标准权值函数中的一个,我们可以使用如下定义的函数:
> (defun make-wf (name &optional
(k (case name
(biweight 4.685)
(cauchy 2.385)
(huber 1.345))))
#'(lambda (x)
(leet ((u (abs (/ r k))))
(case name
(biweight (^ (- 1 (^ (pmin u 1) 2)) 2))
(cauchy (/ 1 (+ 1 (^ u 2))))
(huber (/ 1 (pmax u 1)))))))
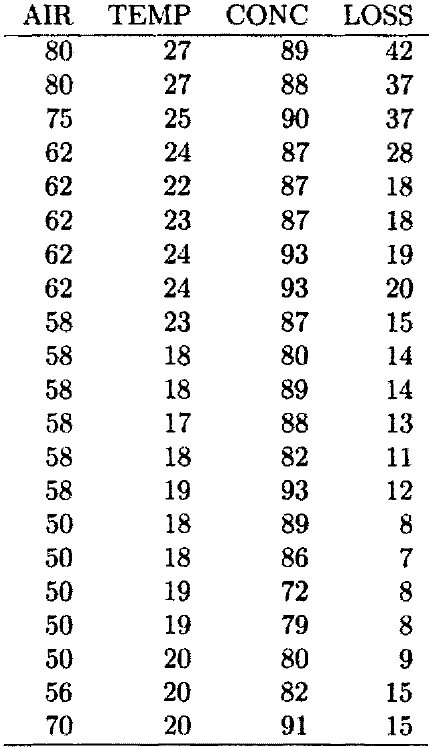
MAKE-WF 作为说明,我们可以用一个例子测试一下这个函数,来自于布朗利的stack loss数据(注: stack loss指从烟道里排除的浪费的热量、不可再生能源和过量的气体,它们来自住宅区通风系统、工厂或者政府建筑物设施)。该数据集由21组观测值组成,它们是关于工厂进行氨氧化成硝酸的操作过程。三个独立变量时AIR,即通过工厂的气流,代表该过程的执行速度;TEMP,即通过吸收塔内部盘管里的循环的制冷水的温度;CONC,一个线性酸循环的浓度的编码。独立变量LOSS,即10次飘到到厂房的氨气的百分比,也就是从吸收塔里逸出的未吸收的部分。
最小二乘拟合可以这样计算:
表5.1 烟道损失数据
> (def air '(80 80 75 62 62 62 62 62 58 58 58 58 58 58 50 50 50 50 50 56 70)) AIR > (def temp '(27 27 25 24 22 23 24 24 23 18 18 17 18 19 18 18 19 19 29 29 29)) TEMP > (def conc '(89 88 90 87 87 87 93 93 87 80 89 88 82 93 89 86 72 79 80 82 91)) CONC > (def loss '(42 37 37 28 18 18 19 20 15 14 14 13 11 12 8 7 8 8 9 15 15)) LOSS > (regression-model (list air temp conc) loss) Least Squares Estimates: Constant -34.8780 (15.8781) Variable 0 1.04201 (0.139894) Variable 1 8.517019E-2 (0.270213) Variable 2 -0.144541 (0.206340) R Squared: 0.851471 Sigma hat: 4.25193 Number of cases: 21 Degrees of freedom: 17 #<Object: 1416818, prototype = REGRESSION-MODEL-PROTO>使用Huber权值函数的稳健回归模型的系数是:
> (robust-coefs (list air temp conc) loss (make-wf 'huber)) (-41.0267 0.829344 0.926232 -0.127856)已经获取这些系数了,我们可以返回去计算在最后的拟合里要用到的权值,并且检查是否存在某些点收到的权重特别的小。在这种情况下,收到的权重小于0.5的点的下标分别是0、2、3和20,这些点通常被当成该数据集里可能的异常值。
练习 5.2
略。
练习 5.3
略。