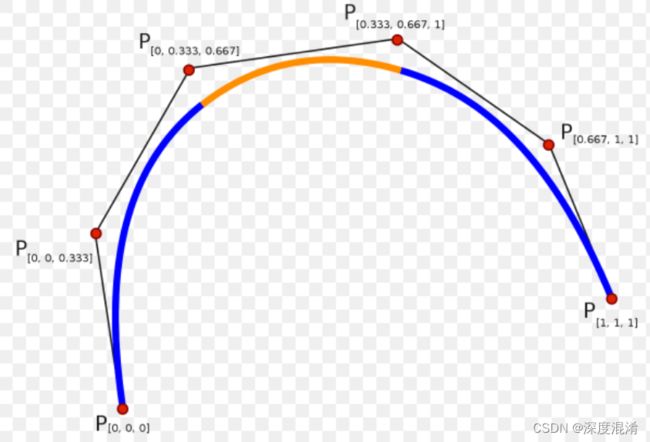
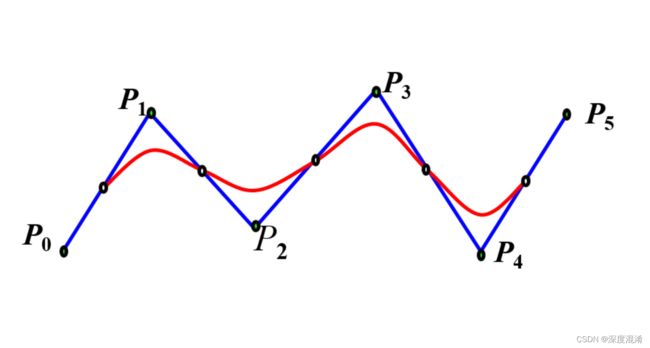
C#,计算几何,鼠标点击绘制 (二维,三次)B样条曲线的代码
B样条(B-Spline)是常用的曲线拟合与插值算法之一。
这里给出在 Form 的 图像 Picturebox 组件上,按鼠标点击点绘制 (三次)B样条曲线的代码。
2022-12-05 修改了代码。
1 文本格式
using System;
using System.Data;
using System.Linq;
using System.Text;
using System.Drawing;
using System.Collections;
using System.Collections.Generic;
using System.ComponentModel;
using System.Threading.Tasks;
using System.Windows.Forms;
namespace Legalsoft.Truffer.Algorithm;
{
public partial class Form1 : Form
{
public double[] splinex = new double[1001];
public double[] spliney = new double[1001];
public point[] pt = new point[6];
public int no_of_points = 0;
///
/// Prints a dot at the place whrere the mouseup event occurs
///
///
///
private void pictureBox1_MouseUp(object sender, MouseEventArgs e)
{
Graphics g = pictureBox1.CreateGraphics();
Color cl = Color.DarkBlue;
g.DrawLine(new Pen(cl, 2), e.X-3, e.Y, e.X + 3, e.Y);
g.DrawLine(new Pen(cl, 2), e.X, e.Y-3, e.X, e.Y + 3);
g.DrawString(no_of_points+"", new Font("宋体",12), new SolidBrush(Color.Red), e.X, e.Y);
}
///
/// At each mousedown event the the no of points is calculated
/// if the value is more than 3 then the curve is drawn
///
///
///
private void pictureBox1_MouseDown(object sender, MouseEventArgs e)
{
if (no_of_points > 3)
{
pt[0] = pt[1];
pt[1] = pt[2];
pt[2] = pt[3];
pt[3].X = e.X;
pt[3].Y = e.Y;
double temp = Math.Sqrt(Math.Pow(pt[2].X - pt[1].X, 2F) + Math.Pow(pt[2].Y - pt[1].Y, 2F));
int interpol = System.Convert.ToInt32(temp);
bspline(pt[0], pt[1], pt[2], pt[3], interpol);
int width = 2;
Graphics g = pictureBox1.CreateGraphics();
Color cl = Color.Blue;
int x, y;
for (int i = 0; i <= interpol - 1; i++)
{
x = System.Convert.ToInt32(splinex[i]);
y = System.Convert.ToInt32(spliney[i]);
g.DrawLine(new Pen(cl, width), x - 1, y, x + 1, y);
g.DrawLine(new Pen(cl, width), x, y - 1, x, y + 1);
}
}
else
{
pt[no_of_points].X = e.X;
pt[no_of_points].Y = e.Y;
}
no_of_points++;
}
///
/// calculating the values using the algorithm
///
///
///
///
///
///
public void bspline(point p1, point p2, point p3, point p4, int divisions)
{
double[] a = new double[5];
double[] b = new double[5];
a[0] = (-p1.X + 3 * p2.X - 3 * p3.X + p4.X) / 6.0;
a[1] = (3 * p1.X - 6 * p2.X + 3 * p3.X) / 6.0;
a[2] = (-3 * p1.X + 3 * p3.X) / 6.0;
a[3] = (p1.X + 4 * p2.X + p3.X) / 6.0;
b[0] = (-p1.Y + 3 * p2.Y - 3 * p3.Y + p4.Y) / 6.0;
b[1] = (3 * p1.Y - 6 * p2.Y + 3 * p3.Y) / 6.0;
b[2] = (-3 * p1.Y + 3 * p3.Y) / 6.0;
b[3] = (p1.Y + 4 * p2.Y + p3.Y) / 6.0;
splinex[0] = a[3];
spliney[0] = b[3];
for (int i = 1; i <= divisions - 1; i++)
{
double t = System.Convert.ToSingle(i) / System.Convert.ToSingle(divisions);
splinex[i] = (a[2] + t * (a[1] + t * a[0])) * t + a[3];
spliney[i] = (b[2] + t * (b[1] + t * b[0])) * t + b[3];
}
}
}
}
2 代码格式
using System;
using System.Data;
using System.Linq;
using System.Text;
using System.Drawing;
using System.Collections;
using System.Collections.Generic;
using System.ComponentModel;
using System.Threading.Tasks;
using System.Windows.Forms;
namespace Legalsoft.Truffer.Algorithm;
{
public partial class Form1 : Form
{
public double[] splinex = new double[1001];
public double[] spliney = new double[1001];
public point[] pt = new point[6];
public int no_of_points = 0;
///
/// Prints a dot at the place whrere the mouseup event occurs
///
///
///
private void pictureBox1_MouseUp(object sender, MouseEventArgs e)
{
Graphics g = pictureBox1.CreateGraphics();
Color cl = Color.DarkBlue;
g.DrawLine(new Pen(cl, 2), e.X-3, e.Y, e.X + 3, e.Y);
g.DrawLine(new Pen(cl, 2), e.X, e.Y-3, e.X, e.Y + 3);
g.DrawString(no_of_points+"", new Font("宋体",12), new SolidBrush(Color.Red), e.X, e.Y);
}
///
/// At each mousedown event the the no of points is calculated
/// if the value is more than 3 then the curve is drawn
///
///
///
private void pictureBox1_MouseDown(object sender, MouseEventArgs e)
{
if (no_of_points > 3)
{
pt[0] = pt[1];
pt[1] = pt[2];
pt[2] = pt[3];
pt[3].X = e.X;
pt[3].Y = e.Y;
double temp = Math.Sqrt(Math.Pow(pt[2].X - pt[1].X, 2F) + Math.Pow(pt[2].Y - pt[1].Y, 2F));
int interpol = System.Convert.ToInt32(temp);
bspline(pt[0], pt[1], pt[2], pt[3], interpol);
int width = 2;
Graphics g = pictureBox1.CreateGraphics();
Color cl = Color.Blue;
int x, y;
for (int i = 0; i <= interpol - 1; i++)
{
x = System.Convert.ToInt32(splinex[i]);
y = System.Convert.ToInt32(spliney[i]);
g.DrawLine(new Pen(cl, width), x - 1, y, x + 1, y);
g.DrawLine(new Pen(cl, width), x, y - 1, x, y + 1);
}
}
else
{
pt[no_of_points].X = e.X;
pt[no_of_points].Y = e.Y;
}
no_of_points++;
}
///
/// calculating the values using the algorithm
///
///
///
///
///
///
public void bspline(point p1, point p2, point p3, point p4, int divisions)
{
double[] a = new double[5];
double[] b = new double[5];
a[0] = (-p1.X + 3 * p2.X - 3 * p3.X + p4.X) / 6.0;
a[1] = (3 * p1.X - 6 * p2.X + 3 * p3.X) / 6.0;
a[2] = (-3 * p1.X + 3 * p3.X) / 6.0;
a[3] = (p1.X + 4 * p2.X + p3.X) / 6.0;
b[0] = (-p1.Y + 3 * p2.Y - 3 * p3.Y + p4.Y) / 6.0;
b[1] = (3 * p1.Y - 6 * p2.Y + 3 * p3.Y) / 6.0;
b[2] = (-3 * p1.Y + 3 * p3.Y) / 6.0;
b[3] = (p1.Y + 4 * p2.Y + p3.Y) / 6.0;
splinex[0] = a[3];
spliney[0] = b[3];
for (int i = 1; i <= divisions - 1; i++)
{
double t = System.Convert.ToSingle(i) / System.Convert.ToSingle(divisions);
splinex[i] = (a[2] + t * (a[1] + t * a[0])) * t + a[3];
spliney[i] = (b[2] + t * (b[1] + t * b[0])) * t + b[3];
}
}
}
}