SVM支持向量机（二）拉格朗日、KKT、松弛变量与惩罚函数

一、拉格朗日乘子法如何工作

    上篇笔记说道，SVM要求几何上的间隔最大问题，演变成了凸优化问题。先说一下为什么是凸优化，因为我们要求最大值的函数，是一个凸函数，在凸函数上两点间取一条直线，会发现函数上的点，总在直线之上，主要是因为||w||^2展开之后都是2次方。怎样解决这样的凸优化问题呢？我们从最简单的例子开始。首先构造一个类似的例子，然后我们用拉格朗日乘子法解决他，了解拉格朗日乘子法的工作原理。

    假设我们要求f(x,y) = x^2 + y^2 的最小值。我们直接求导，令导数（或者说是梯度）都等于0就好了，既 2x=0，2y=0，也就是说x和y都取0的时候，f(x,y)达到最小值。梯度可以理解成，所有变量偏导数组成的向量，可以参考我另一篇博客http://my.oschina.net/u/1047640/blog/283128。

    此时我们加上限制条件，y=x+2，再求f(x,y)的最小值。该怎么求呢？首先我们构造拉格朗日函数，用大写L表示，把原函数写在最前面，然后把限制条件作为一个表达式加到后面，同时乘以拉格朗日乘子λ。我们构造出来的拉格朗日函数是
L(x,y,λ) = x^2 + y^2 + λ(y - x -2)。 求拉格朗日函数的梯度，εx = 2x-λ , εy = 2y+λ，另他们都等于0，而且y=x+2所以求的x=-1,y=1的时候，f(x,y)取到最小值。为什么拉格朗日函数在梯度为0的时候，既能满足限制条件，又能使目标函数在限制条件下是最优的呢？我们可以从几何意义上直观的感受到。

不过这张图和我们上面的例子稍有不同，其中f(x,y)可以看成目标函数，而g(x,y)可以看作限制条件，上面的例子中我们的限制条件是一条直线，图里换成了曲线，不过并不影响我们理解。假设f(x,y)=x^2 + y^2，在没有仍和约束条件下，它可以收缩。现在引入了限制条件，这个圆在尽可能的缩小的时候，必须和限制条件g(x,y)有交点。从几何的直观意义上来讲，当f(x,y)在限制条件下取到最小值时，f(x,y)和g(x,y)是相切的，因为他们此时只有一个交点。相切意味着什么呢？意味着这两个函数此时共享一条切线，从切线上一点作切线的垂线，垂线所指的方向恰恰是函数的梯度。也就是说，此时f(x,y)和g(x,y)梯度正好成相反的方向。梯度成相反的方向，正好会使拉格朗日函数的梯度等于0，也就是为什么我们求拉格朗日函数的梯度为0时，可以在限制条件下取到最小值。下面用函数式子解释这一点
设f(x,y)是目标函数，g(x,y) = c 是限制条件，c为常量。拉格朗日函数写成L，梯度写成▽
L(x,y,λ) = f(x,y) +λ( g(x,y)-c )
▽L = ▽f(x,y) + λg(x,y)    #因为C为常数，求导时直接销掉
令▽L = 0
则 ▽f(x,y) = -λg(x,y)

    也就是说，取最值的时候，两个函数是相切的，相切就是梯度相反，梯度相反加上一个拉格朗日乘子λ，可以使拉格朗日函数的梯度为0。倒过来说，我们求拉格朗日函数梯度为0时就可以得到目标函数的最值。当然前提条件是目标函数是凸函数，可导，限制条件函数也是可导的。这里只是使用拉格朗日乘子法而已，没有证明。

二、将拉格朗日乘子法应用到支持向量机上

    现在，把拉格朗日乘子法应用到支持向量机的解法上。上一篇笔记讲到，我们的目标是

    我们把下面的限制条件一个个加到目标函数上，得到一个拉格朗日函数。注意这里是N个条件。为什么要减去限制条件，而不是加上呢？其实这里写减号还是加号无所谓，但是，为了变换式子之后方便我们求解，先写成减号。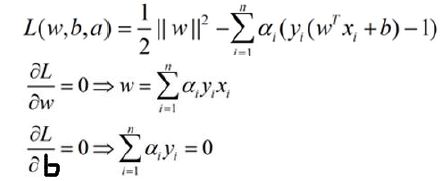

    拉格朗日乘子分别是a1,a2,a3,a4,a5…… 。但是这里已经不是拉格朗日乘子法了。因为拉格朗日乘子法的限制条件是一个等式，而不是不等式。我们这里N个限制条件全是不等式，但是求解的思路和拉格朗日乘子法是类似的。这种针对不等式求最优解的方法叫做KKT条件法。

    w是一个向量，我们求导的时候，展开一个个求导和不对其展开，而是把他当作一个整体来看待，求出来的结果是一样的，令他的偏导数为0 得到 w=∑ai*yi*xi。同理求b的偏导数，得∑aiyi = 0。然后我们再把w和b带回到拉格朗日函数，经过一系列的优化，方程变整齐了，同时，销掉了w和b，未知数只剩下a，也就是一堆拉格朗日乘子。如果我们解出了a，再带回来就可以解出w和b，那么我们就确定了最佳分隔平面，解决了支持向量机问题。下图是计算过程：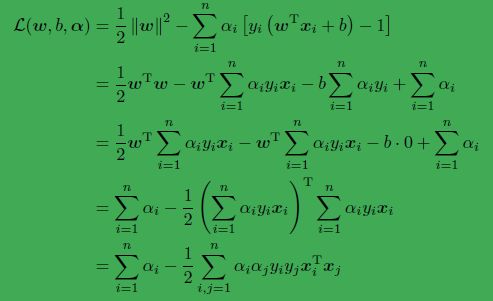

    在此之前，我们是求||w||^2的最小值，构造成拉格朗日函数后，我们仍然是求拉格朗日函数的最小值，因为w和b仍然是目标函数的变量，是我们要优化的目标。但是经过一系列操作，我们消除了这两个变量，虽然拉格朗日函数还是拉格朗日函数，但是，现在不是求最小值了，而是反过来求最大值，因为w和b都已经消除了，现在的变量只有a，a最大才会让||w||的平方最小，所以这个过程已经反过来了。问题从凸优化，转变成了对偶问题。如下图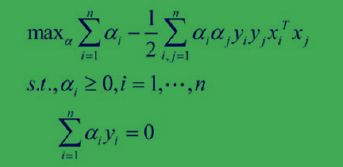

    为什么限制条件中要求a 都大于等于0呢？我理解是因为 ||w||^2这个目标函数是凸函数，所以限制条件必须都在函数的一侧或者另一侧。既然是取||w||^2的最小值，那么限制条件在取到最小值的地方一定都在目标函数的外层。||w||^2，在二维里是一个圆，在三维平面里是一个球……当他是个球，并在限制条件下取到最小值，限制条件一定会都在球外面，而不会内外都有。我们在上面构造拉格朗日函数时减去了限制条件，那么，这里就都大于等于0，反过来则都小于等于0。而下面的∑aiyi = 0是 梯度为0时的条件。

    又进一步，我们将凸优化问题，变换成为拉格朗日函数的对偶问题。后面的博客将讲如何求出a。

三、引入松弛变量解决线性不可分问题

    在上一篇博客里，讲了线性不可分的概念。现在我们引入乘法函数（松弛因子）来看看，有惩罚函数的时候，对偶问题又是怎样的。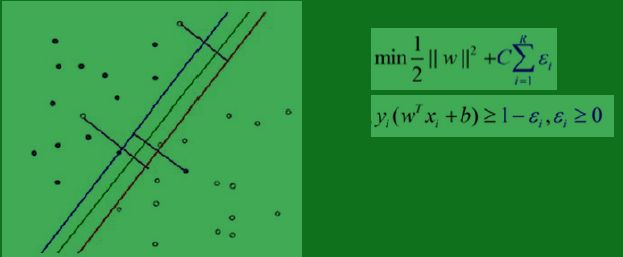

    之前，在线性可分的情况下，我们就是要求||w||^2的最小值。但是在线性不可分的情况下，无论你怎么划分，总是会有点不符合限制条件，也就是说，总有些点y(wx+b) < 1，明明是这个类的却跑到平面的另一边。这样的情况，我们无法求解。于是我们放宽条件，只需要y(wx+b) >= 1 - ε 就行了，也就是说，容许部分点有ε的错判 ，当然原先本来就符合分类的点还是保持以前的限制条件，对他们来说ε = 0。 从图上来看，一个判错的点到自己的类的支撑平面的距离可以看作是ε。光放宽条件当然不行，所以我们对两个平面的间隔距离也要做修正，每出现一个错误，我们就将||w||减去ε*C，为毛要乘以C呢？ 因为(1/2)*||w||^2本来就不是两个类之间的距离，而只是一个衡量距离的指标而已。同时我们认为的指定一个C，可以按我们的要求改变对错误分类的容忍能力。当C很大的时候，分错的点就会更少，但是过拟合的情况可能会比较严重，当C很小的时候，分错的点可能会很多，不过可能由此得到的模型也会不太正确，所以如何选择C是有很多学问的，在大部分情况下就是通过经验尝试得到的。

    引入乘法函数后，我们的目标变为了上图右边的公式。我们同样对这个工作加上拉格朗日乘子，并且做对偶变换。然后我们会发现，处理后的对偶问题和没有引入乘法函数之前，紧紧是a变量多了一个上界，而且这个上界是我们指定的常量。

    我们也可以认为，线性可分是线性不可分的一种情况之一。这是一个更广义的情况。

参考博客
详解拉格朗日乘子法和KKT条件 http://blog.csdn.net/xianlingmao/article/details/7919597
支持向量机通俗导论（理解SVM的三层境界） - 结构之法 算法之道 - 博客频道 - CSDN.NET