Java数据结构-线性表之栈(顺序栈和链栈)
栈的定义:(特殊的线性表)
仅在表的一端进行插入和删除的线性表。允许插入、删除的这一端称为栈顶,另一端称为栈底。表中没有元素时称为空栈。
被称为后进先出的线性表(Last In First Out),简称 LIFO表,或被称为先进后出的线性表(First In Last Out),简称 FILO表。
栈更具存储方式的不同分为两种:顺序栈和链栈。
顺序栈:
- 和顺序表一样,顺序栈也采用数组来存放数据元素;
- 为了保证栈底位置的不变,采用数组下标为0的位置作为顺序栈的栈底。
- 而栈顶指针的最大值为capacity(栈的容量)-1;
- 当栈为空栈时,采用栈顶指针指向-1表示。
下面借图(来自http://www.nowamagic.net/librarys/veda/detail/2271)演示一下:
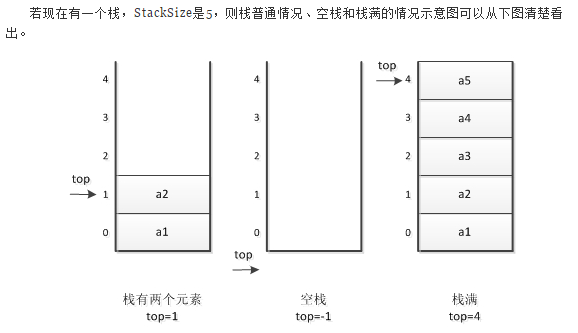
对于顺序栈,数据元素的进栈操作解释如下:
- 栈顶指针top先自增1,给需要进栈的元素腾出内存空间;
- 然后给top对应的数组元素赋值,data[top] = e。size加1
出栈的操作则相反,如下:
- 先获得栈顶指针对应的数组元素的值;
- 然后栈顶指针top减1。size减1
下面是我的Java代码实现:
package com.phn.stack;
/**
* @author 潘海南
* @Email [email protected]
* @TODO 顺序栈
* @date 2015年7月20日
*/
public class FOArrayStack<E> {
//初始化默认栈的存储容量
private static final int DEFUALT_CAPACITY = 100;
//栈中存储数据元素的数组
private Object[] data = null;
//栈的实际大小
private int size;
//栈的栈顶指针
private int top;
//栈的实际容量
private int capacity;
/**
* @TODO 无参构造函数,初始化栈
*/
public FOArrayStack(){
this(DEFUALT_CAPACITY);
}
/**
* @TODO 带参构造函数,初始化栈
* @param initialCapacity 初始化栈的容量
*/
public FOArrayStack(int initialCapacity) {
this.capacity = initialCapacity;
this.data = new Object[initialCapacity];
this.size = 0;
this.top = this.size-1;
}
/**
* @TODO 压入数据元素到栈中
* @param e 数据元素
* @return true
*/
public boolean push(E e){
this.validateCapacity();
this.top++;
this.data[top]=e;
this.size++;
return true;
}
/**
* @TODO 验证栈的实际大小是否已经到达栈实际容量的极限
*/
private void validateCapacity() {
if(this.top==this.capacity-1){
throw new RuntimeException("此栈已满!最大容量="+this.capacity);
}
}
/**
* @TODO 获取栈顶元素,并没有将其弹出栈
* @return e 数据元素
*/
public E peek(){
if(this.isEmpty()){
throw new RuntimeException("此栈为空栈!");
}else{
Object e = new Object();
e = this.data[this.top];
return (E)e;
}
}
/**
* @TODO 获取栈顶元素并弹出栈
* @return e 数据元素
*/
public E pop(){
E e = this.peek();
this.top--;
this.size--;
return e;
}
/**
* @TODO 清空栈
* @return true
*/
public boolean clear(){
while(this.top>=0){
this.data[this.top]=null;
this.top--;
this.size--;
}
return true;
}
@Override
public String toString() {
StringBuffer sb = new StringBuffer("[");
if(this.top!=-1){
sb.append(this.data[this.top]);
int temp = this.top-1;
while(temp>=0){
sb.append(", "+this.data[temp]);
temp--;
}
}
sb.append("]");
return sb.toString();
}
/**
* @TODO 判断栈是否为空
* @return true空 or false不为空
*/
public boolean isEmpty(){
//或者用长度表示
if(this.top==-1){
return true;
}
return false;
}
/**
* @TODO 栈的实际大小
* @return
*/
public int size(){
return this.size;
}
}
我的测试代码:
package com.phn.stack;
/**
* @author 潘海南
* @Email [email protected]
* @TODO 顺序栈测试
* @date 2015年7月20日
*/
public class FOArrayStackTest {
public static void main(String[] args) {
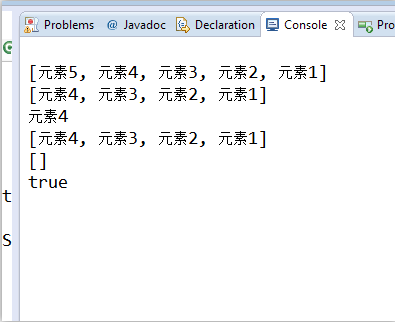
FOArrayStack<String> foas = new FOArrayStack<String>(6);
foas.push("元素1");
foas.push("元素2");
foas.push("元素3");
foas.push("元素4");
foas.push("元素5");
System.out.println(foas);
foas.pop();
System.out.println(foas);
String s = foas.peek();
System.out.println(s);
System.out.println(foas);
foas.clear();
System.out.println(foas);
System.out.println(foas.isEmpty());
}
}
下面扩展一下顺序栈,两栈共享空间:
顺序栈具有单向延伸的特性,在一个程序中如果同时使用了具有相同数据类型的两个栈时可考虑使用一个数组来存储这两个栈,其中栈1的栈底设在该数组的始端,栈2的栈底设在该数组的尾端,两个栈都从各自的端点向数组中部延伸,只有在两个栈的栈顶在数组空间的某一位置相遇时才会产生“上溢”。栈1在入栈操作时栈顶指针top1++,出栈操作时top1–;栈2在入栈操作时栈顶指针top2–,出栈操作时top2++。
链栈:
- 同单链表类似,只不过链栈只能从栈顶插入数据;
- 因此可以将单链表的头指针作为链栈的栈顶指针,而去掉单链表的头结点,这样得到的就是链栈了。
- 链栈不同顺序栈,链栈没有容量限制,不存在栈满的情况。空链栈的定义是栈顶指针指向空null。
对于链栈,插入(压栈)操作push解释如下:
- 将需要插入的数据元素放入一个新建立的节点temp中,将temp的next指向topNode;
- 将topNode赋值为temp。size加1
删除(弹出)操作pop解释如下:
- 取出topNode的数据元素e;
- 然后将topNode指向topNode的next节点;size减1。
下面是我的Java实现代码:
package com.phn.stack;
/**
* @author 潘海南
* @Email [email protected]
* @TODO 链栈
* @date 2015年7月20日
*/
public class FOLinkedStack<E> {
//栈顶指针
private FOLinkedNode<E> topNode = null;
//栈的长度
private int size;
/**
* @TODO 无参构造函数,初始化链栈
*/
public FOLinkedStack() {
this.size = 0;
}
/**
* @TODO 获取栈的长度
* @return
*/
public int size() {
return this.size;
}
/**
* @TODO 压入数据元素到栈中
* @param e 要压入的数据元素
* @return true
*/
public boolean push(E e) {
FOLinkedNode<E> temp = new FOLinkedNode<E>();
temp.setE(e);
temp.addNext(this.topNode);
this.topNode = temp;
this.size++;
return true;
}
/**
* @TODO 获取栈顶元素,并没有弹出,还存在栈中
* @return e 获取到的数据元素
*/
public E peek(){
if(this.isEmpty()){
throw new RuntimeException("链栈为空!");
}else{
E e = this.topNode.getE();
return e;
}
}
/**
* @TODO 弹出栈顶数据元素,不在栈中了
* @return e 弹出的数据元素
*/
public E pop(){
E e = this.peek();
this.topNode = this.topNode.next;
this.size--;
return e;
}
/**
* @TODO 栈是否为空
* @return true空 or false不为空
*/
public boolean isEmpty(){
if(this.topNode==null){
return true;
}
return false;
}
@Override
public String toString() {
StringBuffer sb = new StringBuffer("[");
if(this.topNode!=null){
sb.append(this.topNode.getE());
FOLinkedNode<E> temp =new FOLinkedNode<E>();
temp = this.topNode.next;
while(temp!=null){
sb.append(","+temp.getE());
temp = temp.next;
}
}
sb.append("]");
return sb.toString();
}
}
链栈节点类:
package com.phn.stack;
public class FOLinkedNode<E> {
private E e;// 结点中存放的数据
FOLinkedNode() {
}
FOLinkedNode(E e) {
this.e = e;
}
FOLinkedNode<E> next;// 用来指向该结点的下一个结点
// 设置下一节点的值
void addNext(FOLinkedNode<E> node) {
next = node;
}
public E getE() {
return e;
}
public void setE(E e) {
this.e = e;
}
@Override
public String toString() {
return e.toString();
}
}
下面是我的测试代码:
public static void main(String[] args) {
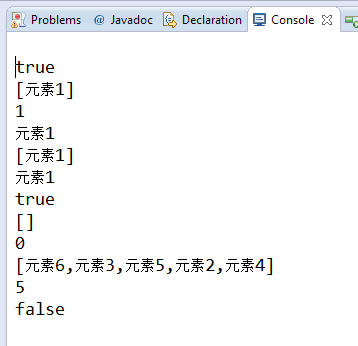
FOLinkedStack<String> fols = new FOLinkedStack<String>();
System.out.println(fols.isEmpty());
fols.push("元素1");
System.out.println(fols);
System.out.println(fols.size());
System.out.println(fols.peek());
System.out.println(fols);
System.out.println(fols.pop());
System.out.println(fols.isEmpty());
System.out.println(fols);
System.out.println(fols.size());
fols.push("元素4");
fols.push("元素2");
fols.push("元素5");
fols.push("元素3");
fols.push("元素6");
System.out.println(fols);
System.out.println(fols.size());
System.out.println(fols.isEmpty());
}
顺序栈和链栈的比较:
- 两种栈都是“先进后出”(或者称之为“后进先出”)的特点,只能在栈顶进行操作,所以时间复杂度为常量O(1);
- 顺序栈初始化需要分配存储空间,分配过大则浪费,过小则溢出;
- 链栈初始化不需要分配空间,不过需要在分配一个指针域,存在结构性开销,但是没有长度限制。
应用建议:
如果栈的使用过程中元素变化不可预料,有时很小,有时非常大,那么最好是用链栈,反之,如果它的变化在可控范围内,建议使用顺序栈会更好一些。
使用栈的原因:栈的引入简化了程序设计的问题,划分了不同关注层次,使得思考范围缩小,更加聚焦于我们要解决的问题核心。
版权声明:本文为博主原创文章,如需转载请注明出处并附上链接,谢谢。