《具体数学》1.3递归(三)
文章开头:先吐槽一下长春的天气,冬天是一星期有6天在下雪,现在算是夏天了吧,动不动下雨下冰雹,天气变化的有点快,还有就是学校的妹子,分为女神和女屌丝,女神一般在长春流行穿风衣,女屌丝一般流行穿牛仔系列,最后吐槽一下,我曾经的喜欢过的人变了,唏嘘不已,好了吐槽完毕,这一篇介绍一下递归的最后一个故事Josephus Circle(约瑟夫环问题),这个部分有点多估计得分两次了。。。。
1.3Josephus Circle(约瑟夫环问题)
这本书还是老规矩,先以故事引出问题:这最后的例子是一个古老问题的变型,它是以公元一世纪著名历史学家Flavius Josephs命名的。传说是Josephus的数学才干让他逃过一劫。
在犹太人和罗马人战争期间,Josephs等41个犹太反抗者陷入包围。他们宁死不做俘虏,决定围成一个圆圈,每次由剩下的人中的第三个自杀,直到所有人都死去为止。
Josephus和他的1个朋友认为,自杀是愚蠢的。因此他很快地算出死亡之圈中他俩应该站的位置(当然,是两个应该最后自杀的位置,没有人监督他们是否自杀,所以你懂得)
我们的问题是,从编号为1到n的围成一圈的人开始,依次排除剩下的人中的第2个(注意:是从当前“指针”开始),直到仅剩1个幸存者。下面是n = 10的情况:
排除次序是2,4,6,8,10,3,7,1,9。因此5幸存。
问题目标是:如何确定幸存者的号码J (n)?
我们刚才看到J(10)=5.我们可能猜测当n是偶数时J(n)=n/2;而且情形n=2支持了猜测:J(2)=1
但对于n=4,n=6猜测失败,从上面的表看来,J(n)都是奇数,因此将其作为新的猜想:事实上第1轮筛选就排除了所有的偶数,因此猜想成立。
另外还观察到,若n是偶数,那么在做完第1轮筛选之后,剩下的情形和最初的开始情况是非常类似的,但是人数要少一半,而且编号也有所不同。
假设原先有2n个人,在第1轮筛选之后,剩下的情况是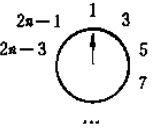
此时圆圈剩下了n个人:1、3、5、7、……、2n – 3、2n – 1。而且“指针”又回到了1的位置。这与最初有n个人的情形是相同的,区别仅在于编号有变化。
编号的变化会带来什么影响?
从编号1开始,下1个被排除的人是3,其后的筛选过程与n个人的情形一致:
当前的情形:2、4、6、8、……(差为2的等差数列)
n个人的情形: 3、7、11、15(差为4的等差数列)
相同点:人数相同
不同点:编号变为2倍减1
注意到,幸存者J(2n)必然从当前剩下的人中出现,因此:
J(2n) = 2J(n) – 1
其实,我们对于人数为奇数页可以得到J(2n+1)=2J(n)+1
到目前为止,我们得到了两个“递归”色彩的式子:
J(2n) = 2J(n) - 1
J(2n + 1) = 2J(n) + 1
上面涵盖了所有“偶数”和“奇数” ,即所有正整数,但还缺少boundary value,作为“递归系统”的第一推动力。
很简单,J(1) = 1(最后剩下1个人,不必再筛选)。这样就得到了完整的J的递归方程。
这个递归方程的效率非常高,因为每次将n缩小至少1/2。例如,我们用19次就能计算出J(1000000):
但如果像上面那样就完 了,这本书真的很厉害,有好多新的思想和套路
但是无论从数学的完美意义,还是实际的计算效率上来考虑,最好找到闭形式解。我们仍然使用“猜想证明”思路来求解封闭形式解。首先根据递归方程,对较小的n建立J(n)表:
可以发现什么规律?(若把n记为形式n=2^m+l,其中2^m是不超过n的2的最大幂,而l则是留下的量)
1、每隔若干个位置就从1开始
2、每次从1开始的子序列都是级差为2的等差数列
3、每个子序列的长度是递增的
继续观察,可以看到:
1、第1子序列长度为1,此后长度为2、4、8、……
(谨慎怀疑子序列长度构成比值为2的等比数列!!)
2、如果上述怀疑成立,那么我们只要知道当前n处于第几个子序列的第几个位置,就能够从1逐渐累加得到J(n)了!!!
继续找n和J(n)的数量关系:
假设n之前已经有m个子序列,而n是第(m+1)个子序列的第l个位置,那么显然有
J(n) = 1 + 2(l - 1)
n与m、l之间有什么关系呢?
n之前的整数数量为(1 + 2 + 4 + …… + 2^m-1) + (l - 1),因此有
n = (2^m – 1) + l = 2^m + (l – 1)
最后我们可以猜测得到封闭形式为:J(2^m+l) = 2l + 1(m>=0,0<=l<2^m)
(注意,若2^m<=n<2^m+1,则剩余部分l=n-2^m满足0<=l<2^m+1-2^m=2^m)
要证明:J(2^m+l) = 2l + 1(m>=0,0<=l<2^m)这肯定要用到数学归纳法了,但是这里是对m归纳。当m=0时,我们一定有l=0;
因此递归式基础化为J(1)=1,归纳步还分为两部分,依赖于l是偶数还是奇数,若m>0和2^m+l=2n,则 l是偶数并由式J(2n) = 2J(n) - 1和归纳假设可得
J(2^m+l)=2J(2^m-1+l/2)-1=2(2l/2+1)-1=2l+1,这恰好是我们要的,同理可得,奇数情形,完成归纳,这次我们计算J(100),此时我们得到100=2^6+36,所以J(100)=2*36+1=73(其实,在这里我已经觉得很厉害了,下面的更厉害)
大师发现解中2的幂起了重要作用,所以自然要看二进制表示n和J(n),假设n的二进制展开为
n=(bmbm-1...b1b0)2;
也就是说,n=bm2^m+bm-12^m-1+...+b12+b0,其中每个bi是0或1,且其中的第一位bm是1.想到n=2^m+1,我们相继得到
n=(1bm-1bm-2...b1b0)2,l=(0bm-1bm-2...b1b0)2,2l=(bm-1bm-2...b1b01)2,2l+1=(bm-1bm-2...b1b01)2,J(n)=(bm-1bm-2...b1b0bm)2
最后一步是由J(n)=2l+1和bm=1而得出的所以我们证明了J((bmbm-1...b1b0)2)=(bm-1...b1b0bm)2;
也就是说,以计算机程序设计的用语,循环左移一位我们从n取得J(n)不可思议,例如若n=100=(1100100)2,则J(n)=J((1100100)2)=(1001001)2,它是64+8+1=73。
好了先就写到这了,感觉这本书在数学上真的是下了很多功夫,一步一步的引导我们去阅读与思考,有点上瘾了,我怎么了,等过几天,再把另一部分补上,因为有点多,讲约瑟夫这块。。。
