数据结构 (七) 树
7.1 树的概念与表示
7.1.1 树的定义及相关术语
1.树的定义
树(Tree)是n(n≥0)个有限数据元素的集合。当n=0 时,称这棵树为空树。在一棵非树T 中:
(1)有一个特殊的数据元素称为树的根结点,根结点没有前驱结点。
(2)若n>1,除根结点之外的其余数据元素被分成m(m>0)个互不相交的集合T1,T2,…,Tm,其中每一个集合Ti(1≤i≤m)本身又是一棵树。树T1,T2,…,Tm 称为这个根结点的子树。
可以看出,在树的定义中用了递归概念,即用树来定义树。因此,树结构的算法类同于二叉树结构的算法,也可以使用递归方法。
树的定义还可形式化的描述为二元组的形式:
其中D 为树T 中结点的集合,R 为树中结点之间关系的集合。
当树为空树时,D=Φ;当树T 不为空树时有:
其中,Root 为树T 的根结点,DF 为树T 的根Root 的子树集合。DF 可由下式表示:
当树T 中结点个数n≤1 时,R=Φ;当树T 中结点个数n>1 时有:
其中,Root 为树T 的根结点,ri 是树T 的根结点Root 的子树Ti 的根结点。
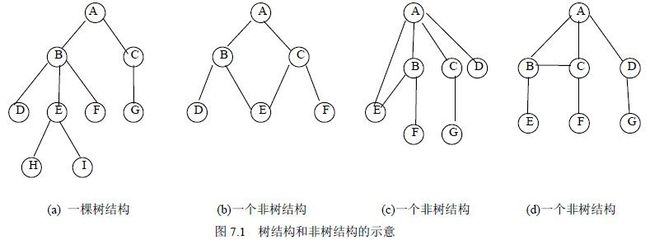
树定义的形式化,主要用于树的理论描述。图7.1(a)是一棵具有9 个结点的树,即T={A,B,C,…,H,I},结点A 为树T 的根结点,除根结点A 之外的其余结点分为两个不相交的集合: T1={B,D,E,F,H,I}和T2={C,G},T1 和T2 构成了结点A 的两棵子树,T1 和T2 本身也分别是一棵树。例如,子树T1 的根结点为B,其余结点又分为两个不相交的集合:T11={D},T12={E,H,I}和T13={F}。
T11、T12 和T13 构成了子树T1 的根结点B 的三棵子树。如此可继续向下分为更小的子树,直到每棵子树只有一个根结点为止。
从树的定义和图7.1(a)的示例可以看出,树具有下面两个特点:
(1)树的根结点没有前驱结点,除根结点之外的所有结点有且只有一个前驱结点。
(2)树中所有结点可以有零个或多个后继结点。
由此特点可知,图7.1(b)、(c)、(d)所示的都不是树结构。
2.相关术语
在二叉树中介绍的有关概念在树中仍然适用。除此之外,再介绍两个关于树的术语。
(1)有序树和无序树。如果一棵树中结点的各子树丛左到右是有次序的,即若交换了某结点各子树的相对位置,则构成不同的树,称这棵树为有序树;反之,则称为无序树。
(2)森林。零棵或有限棵不相交的树的集合称为森林。自然界中树和森林是不同的概念,但在数据结构中,树和森林只有很小的差别。任何一棵树,删去根结点就变成了森林。
7.1.2 树的表示
树的表示方法有以下四种,各用于不同的目的。
1.直观表示法
树的直观表示法就是以倒着的分支树的形式表示,图7.1(a)就是一棵树的直观表示。其特点就是对树的逻辑结构的描述非常直观。是数据结构中最常用的树的描述方法。
2.嵌套集合表示法
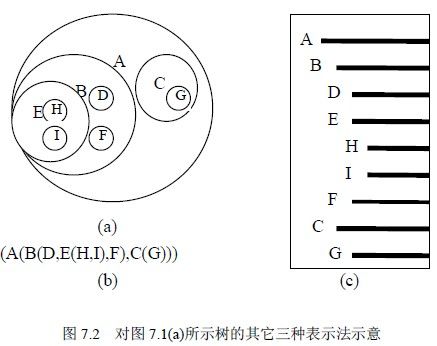
所谓嵌套集合是指一些集合的集体,对于其中任何两个集合,或者不相交,或者一个包含另一个。用嵌套集合的形式表示树,就是将根结点视为一个大的集合,其若干棵子树构成这个大集合中若干个互不相交的子集,如此嵌套下去,即构成一棵树的嵌套集合表示。图7.2 (a)就是一棵树的嵌套集合表示。
3.凹入表示法
树的凹入表示法如图7.2 (c)所示。树的凹入表示法主要用于树的屏幕和打印输出。
4.广义表表示法
树用广义表表示,就是将根作为由子树森林组成的表的名字写在表的左边,这样依次将书表示出来。图7.2 (b)就是一棵树的广义表表示。
7.2 树的基本操作与存储
7.2.1 树的基本操作
树的基本操作通常有以下几种:
(1)Initiate(t)初始化一棵空树t。
(2)Root(x)求结点x 所在树的根结点。
(3)Parent(t,x)求树t 中结点x 的双亲结点。
(4)Child(t,x,i)求树t 中结点x 的第i 个孩子结点。
(5)RightSibling(t,x)求树t 中结点x 的第一个右边兄弟结点。
(6)Insert(t,x,i,s)把以s 为根结点的树插入到树t 中作为结点x 的第i 棵子树。
(7)Delete(t,x,i)在树t 中删除结点x 的第i 棵子树。
(8)Tranverse(t)是树的遍历操作,即按某种方式访问树t 中的每个结点,且使每个结点只被访问一次。
7.2.2 树的存储结构
在计算机中,树的存储有多种方式,既可以采用顺序存储结构,也可以采用链式存储结构,但无论采用何种存储方式,都要求存储结构不但能存储各结点本身的数据信息,还要能唯一地反映树中各结点之间的逻辑关系。下面介绍几种基本的树的存储方式。
1.双亲表示法
由树的定义可以知道,树中的每个结点都有唯一的一个双亲结点,根据这一特性,可用一组连续的存储空间(一维数组)存储树中的各个结点,数组中的一个元素表示树中的一个结点,数组元素为结构体类型,其中包括结点本身的信息以及结点的双亲结点在数组中的序号,树的这种存储方法称为双亲表示法。其存储表示可描述为:
#define MAXNODE <树中结点的最大个数>
typedef struct {
elemtype data;
int parent;
}NodeType;
NodeType t[MAXNODE];
图7.1(a)所示的树的双亲表示如图7.3 所示。图中用parent 域的值为-1 表示该结点无双亲结点,即该结点是一个根结点。
树的双亲表示法对于实现Parent(t,x)操作和Root(x)操作很方便,但若求某结点的孩子结点,即实现Child(t,x,i)操作时,则需要查询整个数组。此外,这种存储方式不能反映各兄弟结点之间的关系,所以实现RightSibling(t,x)操作也比较困难。在实际中,如果需要实现这些操作,可在结点结构中增设存放第一个孩子的域和存放第一个右兄弟的域,就能较方便地实现上述操作了。
2.孩子表示法
(1)多重链表法
由于树中每个结点都有零个或多个孩子结点,因此,可以令每个结点包括一个结点信息域和多个指针域,每个指针域指向该结点的一个孩子结点,通过各个指针域值反映出树中各结点之间的逻辑关系。在这种表示法中,树中每个结点有多个指针域,形成了多条链表,所以这种方法又常称为多重链表法。在一棵树中,各结点的度数各异,因此结点的指针域个数的设置有两种方法:
① 每个结点指针域的个数等于该结点的度数;
② 每个结点指针域的个数等于树的度数。
对于方法①,它虽然在一定程度上节约了存储空间,但由于树中各结点是不同构的,各种操作不容易实现,所以这种方法很少采用;方法②中各结点是同构的,各种操作相对容易实现,但为此付出的代价是存储空间的浪费。图7.4 是图7.1(a)所示的树采用这种方法的存储结构示意图。显然,方法②适用于各结点的度数相差不大的情况。树中结点的存储表示可描述为:
#define MAXSON <树的度数>
typedef struct TreeNode {
elemtype data;
struct TreeNode *son[MAXSON];
}NodeType;
对于任意一棵树t,可以定义:NodeType *t;使变量t 为指向树的根结点的指针。
(2)孩子链表表示法
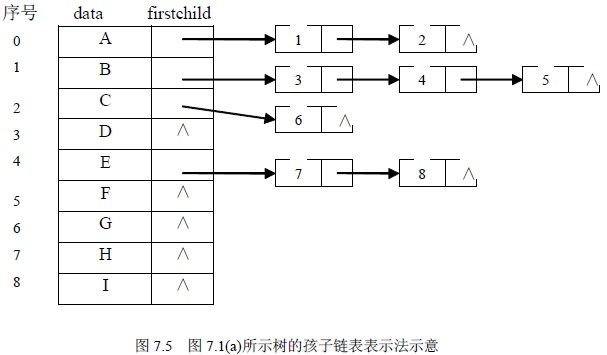
孩子链表法是将树按如图7.5 所示的形式存储。其主体是一个与结点个数一样大小的一维数组,数组的每一个元素有两个域组成,一个域用来存放结点信息,另一个用来存放指针,该指针指向由该结点孩子组成的单链表的首位置。单链表的结构也由两个域组成,一个存放孩子结点在一维数组中的序号,另一个是指针域,指向下一个孩子。
在孩子表示法中查找双亲比较困难,查找孩子却十分方便,故适用于对孩子操作多的应用。
这种存储表示可描述为:
#define MAXNODE <树中结点的最大个数>
typedef struct ChildNode{
int childcode;
struct ChildNode *nextchild;
}
typedef struct {
elemtype data;
struct ChildNode *firstchild;
}NodeType;
NodeType t[MAXNODE];
3.双亲孩子表示法
双亲表示法是将双亲表示法和孩子表示法相结合的结果。其仍将各结点的孩子结点分别组成单链表,同时用一维数组顺序存储树中的各结点,数组元素除了包括结点本身的信息和该结点的孩子结点链表的头指针之外,还增设一个域,存储该结点双亲结点在数组中的序号。图7.6 所示图7.1(a)的树采用这种方法的存储示意图。
4.孩子兄弟表示法
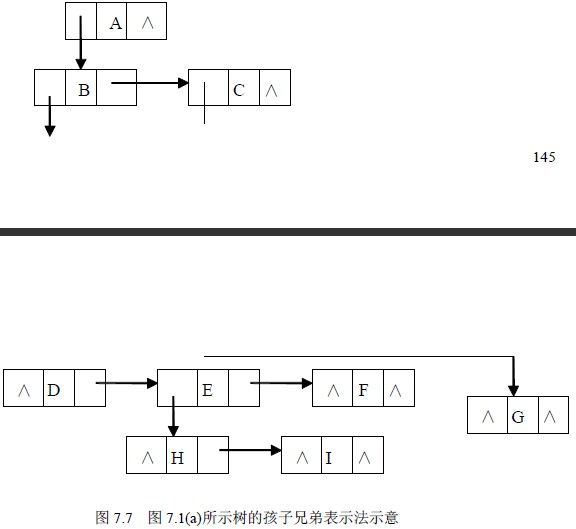
这是一种常用的存储结构。其方法是这样的:在树中,每个结点除其信息域外,再增加两个分别指向该结点的第一个孩子结点和下一个兄弟结点的指针。在这种存储结构下,树中结点的存储表示可描述为:
typedef struct TreeNode {
elemtype data;
struct TreeNode *son;
struct TreeNode *next;
}NodeType;
图7.7 给出了图7.7(a)所示的树采用孩子兄弟表示法时的存储示意图。
7.3 树、森林与二叉树的转换
7.3.1 树转换为二叉树
对于一棵无序树,树中结点的各孩子的次序是无关紧要的,而二叉树中结点的左、右孩子结点是有区别的。为避免发生混淆,我们约定树中每一个结点的孩子结点按从左到右的次序顺序编号。如图7.8 所示的一棵树,根结点A 有B、C、D 三个孩子,可以认为结点B 为A 的第一个孩子结点,结点C 为A 的第二个孩子结点, 结点D 为A 的第三个孩子结点。
将一棵树转换为二叉树的方法是:
(1)树中所有相邻兄弟之间加一条连线。
(2)对树中的每个结点,只保留它与第一个孩子结点之间的连线,删去它与其它孩子结点之间的连线。
(3)以树的根结点为轴心,将整棵树顺时针转动一定的角度,使之结构层次分明。
可以证明,树作这样的转换所构成的二叉树是唯一的。图7.9(a)、(b)、(c)给出了图7.8所示的树转换为二叉树的转换过程示意图。
由上面的转换可以看出,在二叉树中,左分支上的各结点在原来的树中是父子关系,而右分支上的各结点在原来的树中是兄弟关系。由于树的根结点没有兄弟,所以变换后的二叉树的根结点的右孩子必为空。
事实上,一棵树采用孩子兄弟表示法所建立的存储结构与它所对应的二叉树的二叉链表存储结构是完全相同的。
C
∧
∧ D
∧ H
E ∧ F ∧
∧ G
∧ I ∧
B
E
D
F G
7.3.2 森林转换为二叉树
由森林的概念可知,森林是若干棵树的集合,只要将森林中各棵树的根视为兄弟,每棵树又可以用二叉树表示,这样,森林也同样可以用二叉树表示。森林转换为二叉树的方法如下:
(1)将森林中的每棵树转换成相应的二叉树。
(2)第一棵二叉树不动,从第二棵二叉树开始,依次把后一棵二叉树的根结点作为前一棵二叉树根结点的右孩子,当所有二叉树连起来后,此时所得到的二叉树就是由森林转换得到的二叉树。
这一方法可形式化描述为:
如果F={ T1,T2,…,Tm }是森林,则可按如下规则转换成一棵二叉树B=(root,LB,RB)。
(1)若F 为空,即m=0,则B 为空树;
(2)若F 非空,即m≠0,则B 的根root 即为森林中第一棵树的根Root(T1);B 的左子树LB 是从T1 中根结点的子树森林F1={ T11,T12,…,T1m1 }转换而成的二叉树;其右子树RB 是从森林F’={ T2,T3,…,Tm }转换而成的二叉树。
图7.10 给出了森林及其转换为二叉树的过程。
7.3.3 二叉树转换为树和森林
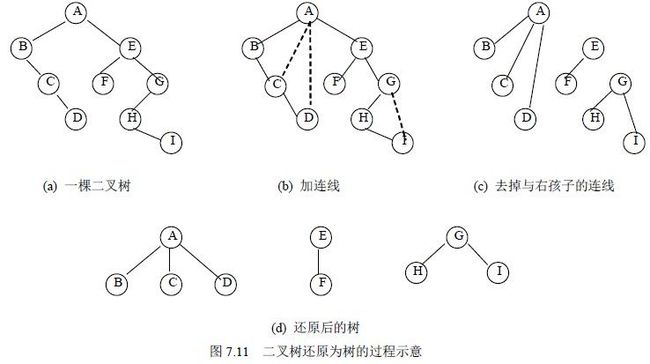
树和森林都可以转换为二叉树,二者不同的是树转换成的二叉树,其根结点无右分支,而森林转换后的二叉树,其根结点有右分支。显然这一转换过程是可逆的,即可以依据二叉树的根结点有无右分支,将一棵二叉树还原为树或森林,具体方法如下:
(1)若某结点是其双亲的左孩子,则把该结点的右孩子、右孩子的右孩子……都与该结点的双亲结点用线连起来;
(2)删去原二叉树中所有的双亲结点与右孩子结点的连线;
(3)整理由(1)、(2)两步所得到的树或森林,使之结构层次分明。
这一方法可形式化描述为:
如果B=(root,LB,RB)是一棵二叉树,则可按如下规则转换成森林F={ T1,T2,…,Tm }。
(1)若B 为空,则F 为空;
(2)若B 非空,则森林中第一棵树T1 的根ROOT(T1)即为B 的根root;T1 中根结点的子树森林F1 是由B 的左子树LB 转换而成的森林;F 中除T1 之外其余树组成的森林F’={ T2,T3,…,Tm }是由B 的右子树RB 转换而成的森林。
图7.11 给出了一棵二叉树还原为森林的过程示意。
7.4 树和森林的遍历
7.4.1 树的遍历
树的遍历通常有以下两种方式。
1.先根遍历
先根遍历的定义为:
(1)访问根结点;
(2)按照从左到右的顺序先根遍历根结点的每一棵子树。
按照树的先根遍历的定义,对图7.8 所示的树进行先根遍历,得到的结果序列为:
A B E F C D G
2.后根遍历
后根遍历的定义为:
(1)按照从左到右的顺序后根遍历根结点的每一棵子树。
(2)访问根结点;
按照树的后根遍历的定义,对图7.8 所示的树进行后根遍历,得到的结果序列为:
7.4.2 森林的遍历
森林的遍历有前序遍历和中序遍历两种方式。1.前序遍历
前序遍历的定义为:
(1)访问森林中第一棵树的根结点;
(2)前序遍历第一棵树的根结点的子树;
(3)前序遍历去掉第一棵树后的子森林。
对于图7.10(a)所示的森林进行前序遍历,得到的结果序列为:
2.中序遍历
中序遍历的定义为:
(1)中序遍历第一棵树的根结点的子树;
(2)访问森林中第一棵树的根结点;
(3)中序遍历去掉第一棵树后的子森林。
对于图7.10(a)所示的森林进行中序遍历,得到的结果序列为:
7.5 树的应用