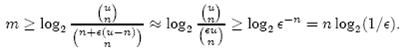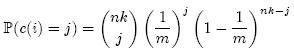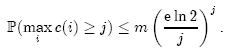Bloom Filter 算法简介

应用场景
在正式介绍Bloom Filter算法之前，先来看看什么时候需要用到Bloom Filter算法。
1. HTTP缓存服务器、Web爬虫等
主要工作是判断一条URL是否在现有的URL集合之中（可以认为这里的数据量级上亿）。
对于HTTP缓存服务器，当本地局域网中的PC发起一条HTTP请求时，缓存服务器会先查看一下这个URL是否已经存在于缓存之中，如果存在的话就没有必要去原始的服务器拉取数据了（为了简单起见，我们假设数据没有发生变化），这样既能节省流量，还能加快访问速度，以提高用户体验。
对于Web爬虫，要判断当前正在处理的网页是否已经处理过了，同样需要当前URL是否存在于已经处理过的URL列表之中。

2. 垃圾邮件过滤
假设邮件服务器通过发送方的邮件域或者IP地址对垃圾邮件进行过滤，那么就需要判断当前的邮件域或者IP地址是否处于黑名单之中。如果邮件服务器的通信邮件数量非常大（也可以认为数据量级上亿），那么也可以使用Bloom Filter算法。

几个专业术语
这里有必要介绍一下False Positive和False Negative的概念（更形象的描述可以阅读第4条参考）。
False Positive中文可以理解为“假阳性”，形象的一点说就是“误报”，后面将会说道Bloom Filter存在误报的情况，现实生活中也有误报，比如说去体检的时候，医生告诉你XXX检测是阳性，而实际上是阴性，也就是说误报了，是假阳性，杀毒软件误报也是同样的概念。
False Negative，中文可以理解为“假阴性”，形象的一点说是“漏报”。医生告诉你XXX检测为阴性，实际上你是阳性，你是有病的（Sorry, it’s just a joke），那就是漏报了。同样杀毒软件也存在漏报的情况。

Bloom Filter算法
好了，终于要正式介绍Bloom Filter算法了。
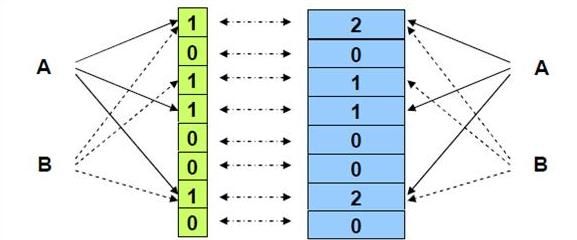
初始状态下，Bloom Filter是一个m位的位数组，且数组被0所填充。同时，我们需要定义k个不同的hash函数，每一个hash函数都随机的将每一个输入元素映射到位数组中的一个位上。那么对于一个确定的输入，我们会得到k个索引。

插入元素：经过k个hash函数的映射，我们会得到k个索引，我们把位数组中这k个位置全部置1（不管其中的位之前是0还是1）

查询元素：输入元素经过k个hash函数的映射会得到k个索引，如果位数组中这k个索引任意一处是0，那么就说明这个元素不在集合之中；如果元素处于集合之中，那么当插入元素的时候这k个位都是1。但如果这k个索引处的位都是1，被查询的元素就一定在集合之中吗？答案是不一定，也就是说出现了False Positive的情况（但Bloom Filter不会出现False Negative的情况）

在上图中，当插入x、y、z这三个元素之后，再来查询w，会发现w不在集合之中，而如果w经过三个hash函数计算得出的结果所得索引处的位全是1，那么Bloom Filter就会告诉你，w在集合之中，实际上这里是误报，w并不在集合之中。

False Positive Rate
Bloom Filter的误报率到底有多大？下面在数学上进行一番推敲。假设HASH函数输出的索引值落在m位的数组上的每一位上都是等可能的。那么，对于一个给定的HASH函数，在进行某一个运算的时候，一个特定的位没有被设置为1的概率是

那么，对于所有的k个HASH函数，都没有把这个位设置为1的概率是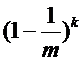

如果我们已经插入了n个元素，那么对于一个给定的位，这个位仍然是0的概率是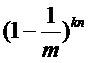

那么，如果插入n个元素之后，这个位是1的概率是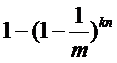

如果对一个特定的元素存在误报，那么这个元素的经过HASH函数所得到的k个索引全部都是1，概率也就是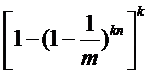

根据常数e的定义，可以近似的表示为：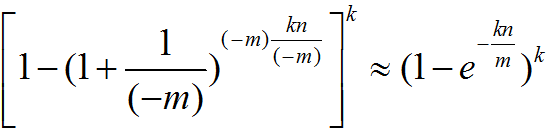

关于误报
有时候误报对实际操作并不会带来太大的影响，比如对于HTTP缓存服务器，如果一条URL被误以为存在与缓存服务器之中，那么当取数据的时候自然会无法取到，最终还是要从原始服务器当中获取，之后再把记录插入缓存服务器，几乎没有什么不可以接受的。
对于安全软件，有着“另可错报，不可误报”的说法，如果你把一个正常软件误判为病毒，对使用者来说不会有什么影响（如果用户相信是病毒，那么就是删除这个文件罢了，如果用户执意要执行，那么后果也只能由用户来承担）；如果你把一个病毒漏判了，那么对用户造成的后果是不可设想的……更有甚者，误报在某种程度上能让部分用户觉得你很专业……

最优的哈希函数个数

既然Bloom Filter要靠多个哈希函数将集合映射到位数组中，那么应该选择几个哈希函数才能使元素查询时的错误率降到最低呢？这里有两个互斥的理由：如果哈希函数的个数多，那么在对一个不属于集合的元素进行查询时得到0的概率就大；但另一方面，如果哈希函数的个数少，那么位数组中的0就多。为了得到最优的哈希函数个数，我们需要根据上一小节中的错误率公式进行计算。

 

先用p和f进行计算。注意到f = exp(k ln(1 − e^−kn/m))，我们令g = k ln(1 − e^−kn/m)，只要让g取到最小，f自然也取到最小。由于p = e^-kn/m，我们可以将g写成

根据对称性法则可以很容易看出当p = 1/2，也就是k = ln2· (m/n)时，g取得最小值。在这种情况下，最小错误率f等于(1/2)^k ≈ (0.6185)^m/n。另外，注意到p是位数组中某一位仍是0的概率，所以p = 1/2对应着位数组中0和1各一半。换句话说，要想保持错误率低，最好让位数组有一半还空着。

 

需要强调的一点是，p = 1/2时错误率最小这个结果并不依赖于近似值p和f。同样对于f’ = exp(k ln(1 − (1 − 1/m)^kn))，g’ = k ln(1 − (1 − 1/m)^kn)，p’ = (1 − 1/m)^kn，我们可以将g’写成

同样根据对称性法则可以得到当p’ = 1/2时，g’取得最小值。

位数组的大小

下面我们来看看，在不超过一定错误率的情况下，Bloom Filter至少需要多少位才能表示全集中任意n个元素的集合。假设全集中共有u个元素，允许的最大错误率为є，下面我们来求位数组的位数m。

 

假设X为全集中任取n个元素的集合，F(X)是表示X的位数组。那么对于集合X中任意一个元素x，在s = F(X)中查询x都能得到肯定的结果，即s能够接受x。显然，由于Bloom Filter引入了错误，s能够接受的不仅仅是X中的元素，它还能够є (u - n)个false positive。因此，对于一个确定的位数组来说，它能够接受总共n + є (u - n)个元素。在n + є (u - n)个元素中，s真正表示的只有其中n个，所以一个确定的位数组可以表示

个集合。m位的位数组共有2^m个不同的组合，进而可以推出，m位的位数组可以表示

   

个集合。全集中n个元素的集合总共有

   

个，因此要让m位的位数组能够表示所有n个元素的集合，必须有

   

即：

   

上式中的近似前提是n和єu相比很小，这也是实际情况中常常发生的。根据上式，我们得出结论：在错误率不大于є的情况下，m至少要等于n log₂(1/є)才能表示任意n个元素的集合。

 

上一小节中我们曾算出当k = ln2· (m/n)时错误率f最小，这时f = (1/2)^k = (1/2)^{mln2 / n}。现在令f≤є，可以推出

这个结果比前面我们算得的下界n log₂(1/є)大了log₂ e ≈ 1.44倍。这说明在哈希函数的个数取到最优时，要让错误率不超过є，m至少需要取到最小值的1.44倍。

总结

在计算机科学中，我们常常会碰到时间换空间或者空间换时间的情况，即为了达到某一个方面的最优而牺牲另一个方面。Bloom Filter在时间空间这两个因素之外又引入了另一个因素：错误率。在使用Bloom Filter判断一个元素是否属于某个集合时，会有一定的错误率。也就是说，有可能把不属于这个集合的元素误认为属于这个集合（False Positive），但不会把属于这个集合的元素误认为不属于这个集合（False Negative）。在增加了错误率这个因素之后，Bloom Filter通过允许少量的错误来节省大量的存储空间。

 

自从Burton Bloom在70年代提出Bloom Filter之后，Bloom Filter就被广泛用于拼写检查和数据库系统中。近一二十年，伴随着网络的普及和发展，Bloom Filter在网络领域获得了新生，各种Bloom Filter变种和新的应用不断出现。可以预见，随着网络应用的不断深入，新的变种和应用将会继续出现，Bloom Filter必将获得更大的发展。

Counting Bloom Filter

 

从前面对Bloom Filter的介绍可以看出，标准的Bloom Filter是一种很简单的数据结构，它只支持插入和查找两种操作。在所要表达的集合是静态集合的时候，标准Bloom Filter可以很好地工作，但是如果要表达的集合经常变动，标准Bloom Filter的弊端就显现出来了，因为它不支持删除操作。

Counting Bloom Filter的出现解决了这个问题，它将标准Bloom Filter位数组的每一位扩展为一个小的计数器（Counter），在插入元素时给对应的k（k为哈希函数个数）个Counter的值分别加1，删除元素时给对应的k个Counter的值分别减1。Counting Bloom Filter通过多占用几倍的存储空间的代价，给Bloom Filter增加了删除操作。下一个问题自然就是，到底要多占用几倍呢？

 

 

我们先计算第i个Counter被增加j次的概率，其中n为集合元素个数，k为哈希函数个数，m为Counter个数（对应着原来位数组的大小）：

上面等式右端的表达式中，前一部分表示从nk次哈希中选择j次，中间部分表示j次哈希都选中了第i个Counter，后一部分表示其它nk – j次哈希都没有选中第i个Counter。因此，第i个Counter的值大于j的概率可以限定为：

上式第二步缩放中应用了估计阶乘的斯特林公式：

在Bloom Filter概念和原理一文中，我们提到过k的最优值为(ln2)m/n，现在我们限制k ≤ (ln2)m/n，就可以得到如下结论：

如果每个Counter分配4位，那么当Counter的值达到16时就会溢出。这个概率为：

这个值足够小，因此对于大多数应用程序来说，4位就足够了。