【算法】最短路径之A*搜索

最短路径之A*搜索

A*算法很久以前就知道，但一直没细究过。可能是因为一直没遇到要找最短路径的场景，没迫切需求吧。

1) 概述

A*搜索（A* search），是启发式搜索（Heuristic）的一种。

首先，搜索是在一个静态节点网络中进行的，例如地图网格，目标则是找到节点间最短路径。而如何更快的找到这条路径，就是A*算法所解决的。当然，不同场景，其他算法可能更好。

而启发式搜索呢，是指优先顺着具有启发性的节点搜索。也就是猜测那些节点可能是到达目标最好的，先进行搜索，称之为最好优先（Best-first）。

既然是要猜测节点是否最优，自然要有一个评估函数，或称为启发式函数，可记为h(n)。

好，到这里的话，可以先给出A*计算每个节点的代价公式了：

f(n) = g(n) + h(n)

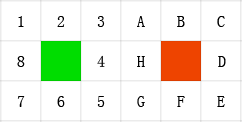
这个g(n)，则是当前节点到起始节点的确切最小代价。假设下面这张图：

以及另外两个条件：

1. 节点为8-邻域的，即绿色节点周围1-8都是相邻可达的。4-邻域的话，就只有2,4,6,8是相邻可达的。（就是能否斜着走）
2. 节点到上下左右（2,4,6,8）代价为10，到对角线节点（1,3,5,7）为14。(1与根号2，用整数替代了)

那么，A到起始绿点的g(n)就为14+10=28。也就是走3A或4A。至于A到目标点的h(n)，则得根据你的评估函数算出来。

A*中h(n)一般采用以下几种空间几何度量，如果假设有(x1,y1)与(x2,y2)两点，那么：

1. 曼哈顿距离（Manhattan distance）: |x1-x2| + |y1-y2|
2. 欧氏距离（Euclidean distance）: sqrt( (x1-x2)^{2 + (y1-y2)}2 )
3. 切比雪夫距离（Chebyshev distance）: max( |x1-x2|, |y1-y2| )

这里如果把h(n)常等于0的话，就是单源最短路径问题了，即Dijkstra算法。就是四散往外找，不做启发式搜索。

2) 原理

“A* Pathfinding for Beginners”讲述的非常清晰，也是Wiki上的外部链接之一。

“A星(A*, A Star)算法详解”是其中文翻译版。

这儿就简单点描述其过程了：

1. 创建一个OPEN列表，并把起始节点加入。
   • OPEN列表是用来存储待处理节点的，随着搜索进行会不断增多。
   • 每次下一步搜索时，会从中检查选取f(n)最小的节点，优先进行搜索。（即步骤3）
2. 创建一个CLOSE列表，为空。
   • CLOSE列表是用来保存OPEN列表每次检查过的节点，以便不再检查。
3. 从OPEN列表中选取f(n)最小的节点，并把它移入CLOSE列表。
4. 检查当前节点周围8-邻域节点：
   • 如果不可通过（障碍物）或者已在CLOSE列表（已检查），略过。不然：
   • 当它不在OPEN列表时，添加进去。并把当前节点作为父节点。计算其f(n)，g(n)与h(n)。
   • 当它已在OPEN列表时，计算新g(n)并与其原g(n)比较，检查是否更好。如果更好的话，则把父节点改为当前节点。h(n)不会变啦，f(n)得重新求下和。
5. 检查若遇到目标节点时，路径被找到。不然重复步骤3，直至OPEN列表为空，即未找到路径。

另外，上述文章内，还提及了很多实现时的注意点。其中值得注意的一点是：二叉堆维护OPEN列表，获取最小节点更快。

3) 运用

也就是实现，现有的库有：

1. JS，PathFinding.js。其还提供了个可视化页面。
2. C++，BGL(Boost Graph Library)也提供了astar_search。

当然，自己实现一遍也是不错的，算是认真学习过了^^。

这儿，我以自己的实现举例。

首先实现语言是C++，参考的是PathFinding.js。二叉堆用的是boost.heap，它提供了以下几种优先队列的实现：

• priority_queue: 优先队列，stl heap的封装，多增加了些模板选项。
• binomial_heap: 二项堆，类似二叉堆，但其支持更快得合并操作。
• fibonacci_heap: 斐波那契堆，比二项堆效率更高。但其结构复杂，常数因子较大。
• pairing_heap: Pairing堆，效率接近斐波那契堆，同时实现简单。
• d_ary_heap: d叉堆，二叉堆的泛化。其拥有d个子节点而非两个。
• skew_heap: 斜堆，左偏树的自调节形式，是具有堆序的二叉树。

比较后，我选择了pairing_heap。

这儿直接上代码段，来回顾下上面提及的过程。

AStarFinder::pnode_vector_t
AStarFinder::FindPath(
        size_type start_x, size_type start_y,
        size_type end_x, size_type end_y,
        const grid_t &grid) const {
    // 从节点网络中拿到起始和目标节点
    pnode_t pstart_node = grid.GetNodeAt(start_x, start_y),
            pend_node = grid.GetNodeAt(end_x, end_y);
    // 额外找邻节点时的选项
    bool allow_diagonal = op_->allow_diagonal,          // 是否允许对角线，4还是8邻域
         dont_cross_corners = op_->dont_cross_corners;  // 是否允许跨越障碍物边角

    // 步骤1：准备OPEN列表。这儿是pairing_heap。
    node_t::heap_t open_list;

    // 同时加入起始节点
    // push the start node into the open list
    pstart_node->opened = true;
    pstart_node->handle = open_list.push(pstart_node);

    // 步骤2的话，这里用节点状态opened与closed来区分，所以不必了。

    pnode_t pnode;
    size_type x = 0, y = 0;
    int ng = 0;
    // 步骤5，所提及的不断重复，直到OPEN列表为空。
    // while the open list is not empty
    while (!open_list.empty()) {
        // 步骤3：选取f(n)最小的节点，设置closed状态。
        // 排序由堆来维护了，只需要pop顶部的节点就行了。
        // pop the position of node which has the minimum `f` value.
        pnode = open_list.top();
        open_list.pop();
        pnode->closed = true;

        // 步骤5，所提及的遇到目标节点，返回节点路径。
        // 节点路径，只需从目标节点不断回溯父节点就行了。
        // if reached the end position, construct the path and return it
        if (pnode == pend_node) {
            return Backtrace<grid_t>(pend_node);
        }

        // 步骤4：查看当前节点的邻节点。
        // get neigbours of the current node
        pnode_vector_t neighbors = grid.GetNeighbors(
            pnode, allow_diagonal, dont_cross_corners);
        BOOST_FOREACH(pnode_t &neighbor, *neighbors) {
            // 关闭的，略去
            if (neighbor->closed) {
                continue;
            }

            x = neighbor->x;
            y = neighbor->y;

            // 计算相对于当前节点，此邻节点的g(n)
            // get the distance between current node and the neighbor
            // and calculate the next g score
            ng = pnode->g + ((x - pnode->x == 0 || y - pnode->y == 0) ? 10 : 14);

            // 如果此邻节点没检查过，或者检查过了但新g(n)更好
            // check if the neighbor has not been inspected yet, or
            // can be reached with smaller cost from the current node
            if (!neighbor->opened || ng < neighbor->g) {
                // 重新赋下f(n)，g(n)与h(n)值
                neighbor->g = ng;
                if (neighbor->h == 0) {  // 还没计算过h(n)时才计算赋值
                    neighbor->h = op_->weight * op_->heuristic(10 * (x - end_x),
                                                               10 * (y - end_y));
                }
                neighbor->f = neighbor->g + neighbor->h;
                // 重新赋下它的父节点
                neighbor->parent = pnode;

                if (!neighbor->opened) {
                    // 没检查过时，得加入OPEN列表。同时push会更新堆。
                    neighbor->opened = true;
                    neighbor->handle = open_list.push(neighbor);
                } else {
                    // 检查过时，由于该邻节点f(n)变了，需要主动更新堆。
                    // the neighbor can be reached with smaller cost.
                    // Since its f value has been updated, we have to
                    // update its position in the open list
                    open_list.update(neighbor->handle);
                }
            }  // end for each neighbor
        }  // end while not open list empty
    }

    // 没找到时，返回个空的。
    // fail to find the path
    return pnode_vector_t();
}

完整代码请见附1。

参考

1. 几种堆(Bin,Fib,Pair)在Dijkstra算法上的效率试验

4) 结语

A*搜索的基本原理还是挺简单易懂的。但如果要深入学习应用的话，不可避免的，还需要了解其各种优化方式、不同场景变化，以及各类衍生变种。

不过呢，对于我目前来说，没这么大必要。也只是看看玩玩，到时要用到再说了。何况有这么多前人栽着树呢，对吧。

附1：样例工程PathFinder

Git：PathFinder。

目录树如下：

PathFinder/
├─benchmark/
├─build/
│  └─PathFinder-msvc.cbp  # test/与boost astar_search例子工程
├─src/
│  ├─core/
│  └─finders/
├─test/
├─third_party/
│  └─boost_1_55_0/
├─tools/
└─visual/
    └─VisualPathFinder/  # A*可视化Qt工程

A*运用仅需src下文件即可，且都是hpp。也就是includepath加上src/与boost_1_55_0/目录就可以了。

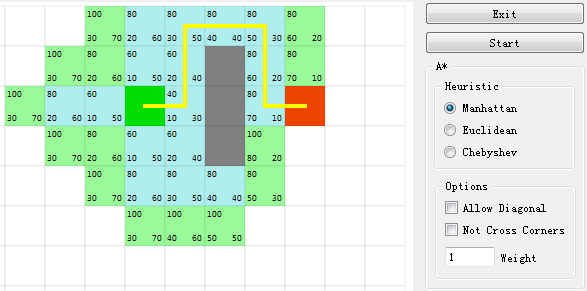
VisualPathFinder/下是Qt工程，A*简单的可视化，大概这个样子：

1. 绿色、红色分别表示起始、目标节点。浅绿色表示opened，浅蓝色表示closed。
2. 数值，左上角为F，左下角为G，右下角为H。
3. 单击起始或目标节点后，再单击其他节点为交换。不然就是切换可不可通过。

然后，右侧有一些可选项目，其他没什么了。没单步，也没标识父节点方向。

原文下载：最短路径之AStar搜索.zip。