马尔可夫模型
马尔可夫个人简介
马尔可夫(1856~1922),苏联数学家。切比雪夫的学生。在概率论、数论、函数逼近论和微分方程等方面卓有成就。
马尔可夫是彼得堡数学学派的代表人物。以数论和概率论方面的工作著称。他的主要著作有《概率演算》等。在数论方面,他研究了连分数和二次不定式理论 ,解决了许多难题 。在概率论中,他发展了矩法,扩大了大数律和中心极限定理的应用范围。马尔可夫最重要的工作是在1906~1912年间,提出并研究了一种能用数学分析方法研究自然过程的一般图式——马尔可夫链。同时开创了对一种无后效性的随机过程——马尔可夫过程的研究。马尔可夫经多次观察试验发现,一个系统的状态转换过程中第n次转换获得的状态常决定于前一次(第n-1次)试验的结果。马尔可夫进行深入研究后指出:对于一个系统,由一个状态转至另一个状态的转换过程中,存在着转移概率,并且这种转移概率可以依据其紧接的前一种状态推算出来,与该系统的原始状态和此次转移前的马尔可夫过程无关。目前,马尔可夫链理论与方法已经被广泛应用于自然科学、工程技术和公用事业中。
马尔可夫模型介绍
Markov Model
马尔可夫模型是一种统计模型,广泛应用在语音识别,词性自动标注,音字转换,概率文法等各个自然语言处理等应用领域。经过长期发展,尤其是在语音识别中的成功应用,使它成为一种通用的统计工具。
到目前为止,它一直被认为是实现快速精确的语音识别系统的最成功的方法。复杂的语音识别问题通过隐含马尔可夫模型能非常简单地被表述、解决,让人们不由由衷地感叹数学模型之妙。
马尔可夫链
因安德烈·马尔可夫(Andrey Markov,1856-1922)得名,是数学中具有马尔可夫性质的离散时间随机过程。该过程中,在给定当前知识或信息的情况下,过去(即当期以前的历史状态)对于预测将来(即当期以后的未来状态)是无关的。
时间和状态都是离散的马尔可夫过程称为马尔可夫链, 简记为Xn=X(n),n=0,1,2…
马尔可夫链是随机变量X1,X2,X3…的一个数列。这些变量的范围,即他们所有可能取值的集合,被称为“状态空间”,而Xn的值则是在时间n的状态。如果Xn + 1对于过去状态的条件概率分布仅是Xn的一个函数,则
P(Xn+1=x∣X0,X1,X2,…,Xn)=P(Xn+1=x∣Xn)
这里x为过程中的某个状态。上面这个恒等式可以被看作是马尔可夫性质。
马尔可夫在1906年首先做出了这类过程 。而将此一般化到可数无限状态空间是由柯尔莫果洛夫在1936年给出的。
马尔可夫链是满足下面两个假设的一种随机过程:
1、t+l时刻系统状态的概率分布只与t时刻的状态有关,与t时刻以前的状态无关;
2、从t时刻到t+l时刻的状态转移与t的值无关。一个马尔可夫链模型可表示为=(S,P,Q),其中各元的含义如下:
1)S是系统所有可能的状态所组成的非空的状态集,有时也称之为系统的状态空间,它可以是有限的、可列的集合或任意非空集。本文中假定S是可数集(即有限或可列)。用小写字母i,j(或Si,Sj)等来表示状态。
2)![]() 是系统的状态转移概率矩阵,其中Pij表示系统在时刻t处于状态i,在下一时刻t+l处于状态i的概率,N是系统所有可能的状态的个数。对于任意i∈s,有
是系统的状态转移概率矩阵,其中Pij表示系统在时刻t处于状态i,在下一时刻t+l处于状态i的概率,N是系统所有可能的状态的个数。对于任意i∈s,有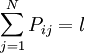 。
。
3)![]() 是系统的初始概率分布,qi是系统在初始时刻处于状态i的概率,满足
是系统的初始概率分布,qi是系统在初始时刻处于状态i的概率,满足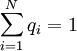 。
。
马尔可夫模型的应用
主要应用于语音识别、音字转换、词性标注。
自然语言是人类交流信息的工具。很多自然语言处理问题都可以等同于通信系统中的解码问题--一个人根据接收到的信息,去猜测发话人要表达的意思。这其实就象通信中,人们根据接收端收到的信号去分析、理解、还原发送端传送过来的信息。比如一个典型的通信系统中:其中s1,s2,s3...表示信息源发出的信号。o1,o2,o3...是接受器接收到的信号。通信中的解码就是根据接收到的信号o1,o2,o3...还原出发送的信号s1,s2,s3...。
其实人们平时在说话时,脑子就是一个信息源。人们的喉咙(声带),空气,就是如电线和光缆般的信道。听众耳朵的就是接收端,而听到的声音就是传送过来的信号。根据声学信号来推测说话者的意思,就是语音识别。这样说来,如果接收端是一台计算机而不是人的话,那么计算机要做的就是语音的自动识别。同样,在计算机中,如果我们要根据接收到的英语信息,推测说话者的汉语意思,就是机器翻译;如果我们要根据带有拼写错误的语句推测说话者想表达的正确意思,那就是自动纠错。那么怎么根据接收到的信息来推测说话者想表达的意思呢?人们可以利用叫做"隐含马尔可夫模型" (HiddenMarkovModel) 来解决这些问题。以语音识别为例,当我们观测到语音信号o1,o2,o3时,要根据这组信号推测出发送的句子s1,s2,s3。显然,人们应该在所有可能的句子中找最有可能性的一个。用数学语言来描述,就是在已知o1,o2,o3,...的情况下,求使得条件概率
P(s1,s2,s3,...|o1,o2,o3....)达到最大值的那个句子s1,s2,s3,...
当然,上面的概率不容易直接求出,于是人们可以间接地计算它。利用贝叶斯公式并且省掉一个常数项,可以把上述公式等价变换成
P(o1,o2,o3,...|s1,s2,s3....)*P(s1,s2,s3,...)
其中
P(o1,o2,o3,...|s1,s2,s3....)表示某句话s1,s2,s3...被读成o1,o2,o3,...的可能性,而
P(s1,s2,s3,...)表示字串s1,s2,s3,...本身能够成为一个合乎情理的句子的可能性,所以这个公式的意义是用发送信号为s1,s2,s3...这个数列的可能性乘以s1,s2,s3...本身可以一个句子的可能性,得出概率。
(读者读到这里也许会问,你现在是不是把问题变得更复杂了,因为公式越写越长了。别着急,现在就来简化这个问题。)人们在这里做两个假设:
第一,s1,s2,s3,...是一个马尔可夫链,也就是说,si只由si-1决定;
第二,第i时刻的接收信号oi只由发送信号si决定(又称为独立输出假设,即P(o1,o2,o3,...|s1,s2,s3....)=P(o1|s1)*P(o2|s2)*P(o3|s3)...。
那么人们就可以很容易利用算法Viterbi找出上面式子的最大值,进而找出要识别的句子s1,s2,s3,...。
满足上述两个假设的模型就叫隐含马尔可夫模型。我们之所以用“隐含”这个词,是因为状态s1,s2,s3,...是无法直接观测到的。
隐含马尔可夫模型的应用远不只在语音识别中。在上面的公式中,如果我们把s1,s2,s3,...当成中文,把o1,o2,o3,...当成对应的英文,那么人们就能利用这个模型解决机器翻译问题;如果我们把o1,o2,o3,...当成扫描文字得到的图像特征,就能利用这个模型解决印刷体和手写体的识别。
P(o1,o2,o3,...|s1,s2,s3....)根据应用的不同而又不同的名称,在语音识别中它被称为“声学模型”(AcousticModel),在机器翻译中是“翻译模型”(TranslationModel)而在拼写校正中是“纠错模型”(CorrectionModel)。而P(s1,s2,s3,...)就是我们在系列一中提到的语言模型。
在利用隐含马尔可夫模型解决语言处理问题前,先要进行模型的训练。常用的训练方法由伯姆(Baum)在60年代提出的,并以他的名字命名。隐含马尔可夫模型在处理语言问题早期的成功应用是语音识别。七十年代,当时IBM的FredJelinek(贾里尼克)和卡内基·梅隆大学的JimandJanetBaker(贝克夫妇,李开复的师兄师姐)分别独立地提出用隐含马尔可夫模型来识别语音,语音识别的错误率相比人工智能和模式匹配等方法降低了三倍(从30%到10%)。八十年代李开复博士坚持采用隐含马尔可夫模型的框架,成功地开发了世界上第一个大词汇量连续语音识别系统Sphinx。
马尔可夫模型的使用方法
它可以用来预测具有等时间隔(如一年)的时刻点上各类人员的分布状况。
它是根据历史数据,预测等时间间隔点上的各类人员分布状况。此方法的基本思想上根据过去人员变动的规律,推测未来人员变动的趋势。步骤如下:
①根据历史数据推算各类人员的转移率,迁出转移率的转移矩阵;
②统计作为初始时刻点的各类人员分布状况;
③建立马尔科夫模型,预测未来各类人员供给状况;
使用马尔科夫模型进行人力资源供给预测的关键是确定出人员转移率矩阵表,而在实际预测时,由于受各种因素的影响,人员转移率是很难准确确定出来的,往往都是一种大致的估计,因此会影响到预测结果的准确性。