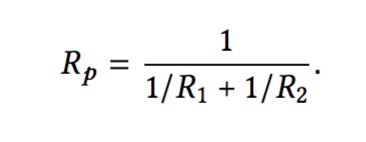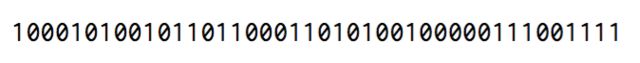SICP:Building Abstractions with Data
2.1 Introduction to Data Abstraction
our programs should use data in such a way as to make no assumptions about the data that are not strictly necessary for performing the task at hand. At the same time, a “concrete” data representation is defined independent of the programs that use the data.The interface between these two parts of our system will be a set of procedures, called selectors and constructors, that implement the abstract data in terms of the concrete representation.
2.1.1 Example: Arithmetic Operations for Rational Numbers
we could express these rules as procedures:
(define (add-rat x y)
(make-rat (+ (* (number x) (denom y))
(* (number y) (denom x)))
(* (denom x) (denom y))))
(define (sub-rat x y)
(make-rat (- (* (numer x) (denom y))
(* (numer y) (denom x)))
(* (denom x) (denom y))))
(define (mul-rat x y)
(make-rat (* (numer x) (numer y))
(* (denom x) (denom y))))
(define (div-rat x y)
(make-rat (* (numer x) (denom y))
(* (denom x) (numer y))))
(define (equal-rat? x y)
(= (* (numer x) (denom y))
(* (numer y) (denom x))))
Pairs
we could use cons, car, cdr to define a compound structure:
> (define x (cons 1 2)) > (define y (cons 3 4)) > (define z (cons x y)) > (car x) 1 > (cdr x) 2 > (car (car z)) 1 > (car (cdr z)) 3
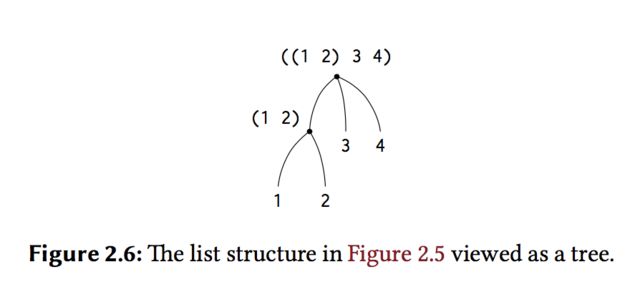
Data objects constructed from paris are called list-structured data.
Representing rational numbers
(define (make-rat n d)
(let ((g (gcd n d)))
(cons (/ n g) (/ d g))))
(define (numer x) (car x))
(define (denom x) (cdr x))
(define (print-rat x)
(newline)
(display (numer x))
(display "/")
(display (denom x)))
(define (add-rat x y)
(make-rat (+ (* (numer x) (denom y))
(* (numer y) (denom x)))
(* (denom x) (denom y))))
(define (sub-rat x y)
(make-rat (- (* (numer x) (denom y))
(* (numer y) (denom x)))
(* (denom x) (denom y))))
(define (mul-rat x y)
(make-rat (* (numer x) (numer y))
(* (denom x) (denom y))))
(define (div-rat x y)
(make-rat (* (numer x) (denom y))
(* (denom x) (numer y))))
(define (equal-rat? x y)
(= (* (numer x) (denom y))
(* (numer y) (denom x))))
(define one-half (make-rat 1 2))
(define one-third (make-rat 1 3))
;5/6
(print-rat (add-rat one-half one-third))
;1/6
(print-rat (mul-rat one-half one-third))
;1/6
(print-rat (sub-rat one-half one-third))
;3/2
(print-rat (div-rat one-half one-third))
2.1.2 Abstraction Barriers
Data-abstraction barriers in the rational-number package:
This simple idea has many advantages. One advantage is that it makes programs much easier to maintain and to modify.
2.1.3 What Is Meant by Data
for the question: what is meant by data? we could not say that the data is defined by some collection of selectors and constructors, it’s not enough! these procedures(selectors and constructors) must fulfill in order to be a valid representation.
for example: how could we define the cons, car and cdr?
(define (cons x y)
(define (dispatch m)
(cond ((= m 0) x)
((= m 1) y)
(else (error "Argument not 0 or 1: CONS" m))))
dispatch)
(define (car z) (z 0))
(define (cdr z) (z 1))

so we can define one as (add-1 zero):
so define two as (add-1 (add-1 zero)):
we now could find that add n is equal to:
so we could define +:
2.1.4 Extended Exercise:Interval Arithmetic
when we accumulate the formula:we known that it could have tolerance, like”6.8 ohms with 10% tolerance”, so it will be: 6.8 - 0.68 ~ 6.8 + 0.68. every value has two endpoints: a lower bound and an upper bound.now we could write the code:
(define (make-interval a b) (cons a b))
(define (lower-bound x) (car x))
(define (upper-bound x) (cdr x))
(define (add-interval x y)
(make-interval (+ (lower-bound x) (lower-bound y))
(+ (upper-bound x) (upper-bound y))))
(define (sub-interval x y)
(make-interval (- (lower-bound x) (upper-bound y))
(- (upper-bound x) (lower-bound y))))
(define (mul-interval x y)
(let ((p1 (* (lower-bound x) (lower-bound y)))
(p2 (* (lower-bound x) (upper-bound y)))
(p3 (* (upper-bound x) (lower-bound y)))
(p4 (* (upper-bound x) (upper-bound y))))
(make-interval (min p1 p2 p3 p4)
(max p1 p2 p3 p4))))
(define (div-interval x y)
(if (and (negative? (lower-bound y)) (positive? (upper-bound y)))
(error "argument y is an interval that spans zero!" y)
(mul-interval
x
(make-interval (/ 1.0 (upper-bound y))
(/ 1.0 (lower-bound y))))))
2.2 Hierarchical Data and the Closure Property
just for the closure property of cons:
2.2.1 Representing Sequences
how could we represented a chain of pairs?like this:
we could use cons, like that:
(define nil '())
(define one-through-four
(cons 1
(cons 2
(cons 3
(cons 4 nil)))))
;1
(car one-through-four)
;(2 3 4)
(cdr one-through-four) but the better is that we could use
list:
the example use list like that:
(define one-through-four (list 1 2 3 4)) ;1 (car one-through-four) ;(2 3 4) (cdr one-through-four)List operations
(define (new-list-ref items n)
(if (= n 0)
(car items)
(new-list-ref (cdr items) (- n 1))))
(define squares (list 1 4 9 16 25))
;16
(new-list-ref squares 3)
;16
(list-ref squares 3)
(define (new-length items)
(if (null? items)
0
(+ 1 (new-length (cdr items)))))
(define odds (list 1 3 5 7))
;4
(new-length odds)
;4
(length odds)
3. append
(define squares (list 1 4 9 16 25))
(define odds (list 1 3 5 7))
(define (new-append list1 list2)
(if (null? list1)
list2
(cons (car list1) (new-append (cdr list1) list2))))
;(1 4 9 16 25 1 3 5 7)
(new-append squares odds)
;(1 4 9 16 25 1 3 5 7)
(append squares odds) 4.
last-pair
(define nil '())
(define (new-last-pair list1)
(define (iter-last-pair lst lst-value)
(if (null? lst)
lst-value
(iter-last-pair (cdr lst) (car lst))))
(iter-last-pair list1 nil))
;34
(new-last-pair (list 23 72 149 34))
;5
(new-last-pair (list 1 2 (list 3 4) 5)) 5.
reverse
(define nil '())
;bad reverse
(define (new-reverse list1)
(if (null? list1)
nil
(list (new-reverse (cdr list1)) (car list1))))
;good reverse
(define (nn-reverse list1)
(define (iter-reverse lst lst-value)
(if (null? lst)
lst-value
(iter-reverse (cdr lst) (cons (car lst) lst-value))))
(iter-reverse list1 nil))
;(((((() 25) 16) 9) 4) 1)
(new-reverse (list 1 4 9 16 25))
;(25 16 9 4 1)
(nn-reverse (list 1 4 9 16 25))
Mapping over lists
One extremely useful operation is to apply some transformation to each element in a list and generate the list of results.
(define nil '())
(define (scale-list items factor)
(if (null? items)
nil
(cons (* (car items) factor)
(scale-list (cdr items)
factor))))
;(10 20 30 40 50)
(scale-list (list 1 2 3 4 5) 10) We can abstract this general idea and capture it as a common pattern expressed as a higher-order procedure:
map
(define nil '())
(define (new-map proc items)
(if (null? items)
nil
(cons (proc (car items))
(map proc (cdr items)))))
;(10 2.5 11.6 17)
(new-map abs (list -10 2.5 -11.6 17))
;(10 2.5 11.6 17)
(map abs (list -10 2.5 -11.6 17))
(define (scale-list items factor)
(new-map (lambda (x) (* x factor))
items))
;(10 20 30 40 50)
(scale-list (list 1 2 3 4 5) 10)
2.2.2 Hierarchical Structures
when we thinks the expression:
(cons (list 1 2) (list 3 4))we could think it like that:
or better as a tree:
(define x (cons (list 1 2) (list 3 4)))
(define (count-leaves x)
(cond ((null? x) 0)
((not (pair? x)) 1)
(else (+ (count-leaves (car x))
(count-leaves (cdr x))))))
;4
(count-leaves x)
Mapping over trees
if we want to map a tree, we could write a process like that:
(define nil '())
(define (scale-tree tree factor)
(cond ((null? tree) nil)
((not (pair? tree)) (* tree factor))
(else (cons (scale-tree (car tree) factor)
(scale-tree (cdr tree) factor)))))
;(10 (20 (30 40) 50) (60 70))
(scale-tree (list 1 (list 2 (list 3 4) 5) (list 6 7)) 10) or we could use
map to finish it:
(define nil '())
(define (scale-tree tree factor)
(map (lambda (sub-tree)
(if (pair? sub-tree)
(scale-tree sub-tree factor)
(* sub-tree factor)))
tree))
;(10 (20 (30 40) 50) (60 70))
(scale-tree (list 1 (list 2 (list 3 4) 5) (list 6 7)) 10)
2.2.3 Sequences as Conventional Interfaces
we write two process.process one takes a tree as argument and computes the sum of the squares of the leaves that are odd:
(define (sum-odd-squares tree)
(cond ((null? tree) 0)
((not (pair? tree))
(if (odd? tree) (square tree) 0))
(else (+ (sum-odd-squares (car tree))
(sum-odd-squares (cdr tree)))))) second process constructs a list of all the even Fibonacci numbers Fib(k):
(define nil '())
(define (even-fibs n)
(define (next k)
(if (> k n)
nil
(let ((f (fib k)))
(if (even? f)
(cons f (next (+ k 1)))
(next (+ k 1))))))) these two process is different, but the work stream is similar:
Sequence Operations
(define (filter-new predicate sequence)
(cond ((null? sequence) nil)
((predicate (car sequence))
(cons (car sequence)
(filter-new predicate (cdr sequence))))
(else (filter-new predicate (cdr sequence)))))
;(1 3)
(filter-new odd? (list 1 2 3 4)) Accumulations can be implemented by:
(define (accumulate op initial sequence)
(if (null? sequence)
initial
(op (car sequence)
(accumulate op initial (cdr sequence)))))
;15
(accumulate + 0 (list 1 2 3 4 5))
;120
(accumulate * 1 (list 1 2 3 4 5))
;(1 2 3 4 5)
(accumulate cons nil (list 1 2 3 4 5)) Generate the sequence of integers in a given range:
(define (enumerate-interval low high)
(if (> low high)
nil
(cons low (enumerate-interval (+ low 1) high))))
;(2 3 4 5 6 7)
(enumerate-interval 2 7) Enumerate the leaves of a tree:
(define (enumerate-tree tree)
(cond ((null? tree) nil)
((not (pair? tree)) (list tree))
(else (append (enumerate-tree (car tree))
(enumerate-tree (cdr tree))))))
;(1 2 3 4 5)
(enumerate-tree (list 1 (list 2 (list 3 4)) 5))
now we could define sum-odd-squares and even-fibs:
(define (sum-odd-squares tree) (accumulate + 0 (map square (filter odd? (enumerate-tree tree))))) (define (even-fibs n) (accumulate cons nil (filter even? (map fib (enumerate-interval 0 n)))))
(define nil '())
(define (accumulate op initial sequence)
(if (null? sequence)
initial
(op (car sequence)
(accumulate op initial (cdr sequence)))))
(define (squares x) (* x x))
(define (fib n)
(cond ((= n 0) 0)
((= n 1) 1)
(else (+ (fib (- n 1))
(fib (- n 2))))))
(define (enumerate-interval n m)
(if (> n m)
nil
(cons n (enumerate-interval (+ n 1) m))))
(define (list-fib-squares n)
(accumulate
cons
nil
(map squares (map fib (enumerate-interval 0 n)))))
;(0 1 1 4 9 25 64 169 441 1156 3025)
(list-fib-squares 10)
(define (product-of-squares-of-odd-elements sequence)
(accumulate * 1 (map squares (filter odd? sequence))))
;225
(product-of-squares-of-odd-elements (list 1 2 3 4 5))

the code is:
(define nil '())
(define (accumulate op initial sequence)
(if (null? sequence)
initial
(op (car sequence)
(accumulate op initial (cdr sequence)))))
(define (enumerate-interval n m)
(if (> n m)
nil
(cons n (enumerate-interval (+ n 1) m))))
(define (flatmap proc seq)
(accumulate append nil (map proc seq)))
(define (prime? n)
(define (iter index)
(cond ((= index n) #t)
((= (remainder n index) 0) #f)
(else (iter (+ index 1)))))
(iter 2))
(define (prime-sum? pair)
(prime? (+ (car pair) (cadr pair))))
(define (make-pair-sum pair)
(list (car pair) (cadr pair) (+ (car pair) (cadr pair))))
(define (prime-sum-pairs n)
(map make-pair-sum
(filter prime-sum? (flatmap
(lambda (i)
(map (lambda (j) (list i j))
(enumerate-interval 1 (- i 1))))
(enumerate-interval 1 n)))))
(prime-sum-pairs 6) the output is:
((2 1 3) (3 2 5) (4 1 5) (4 3 7) (5 2 7) (6 1 7) (6 5 11))when we wish to generate all the permutations of a set S:{1, 2, 3} are {1, 2, 3}, {1, 3, 2}, {2, 1, 3}, {2, 3, 1}, {3, 1, 2}, {3, 2, 1}. we could write the code:
(define (permutations s)
(if (null? s)
(list nil)
(flatmap (lambda (x)
(map (lambda (p) (cons x p))
(permutations (remove x s))))
s)))
(permutations (list 1 2 3)) the output is:
((1 2 3) (1 3 2) (2 1 3) (2 3 1) (3 1 2) (3 2 1))
2.2.4 Example:A Picture Language
2.3 Symbolic Data
2.3.1 Quotation
we could use Quotation to allow us to type in compound objects, using the conventional printed representation for lists:
(define a 1) (define b 2) ;(1 2) (list a b) ;(a b) (list 'a 'b) ;(a 2) (list 'a b) ;a (car '(a b c)) ;(b c) (cdr '(a b c))we could use quotation to write a process: it returns the sublist of the list beginning with the first occurrence of the symbol:
(define (memq-new item x)
(cond ((null? x) false)
((eq? item (car x)) x)
(else (memq-new item (cdr x)))))
;#f
(memq-new 'apple '(pear banana prune))
;(apple pear)
(memq-new 'apple '(x (apple sauce) y apple pear))
2.3.2 Example:Symbolic Differentiation
now we develop the symbolic-differentiation program.

so we could define procedures to implement the following selectors, constructors, and predicates:
so we could define the process deriv:
(define (deriv exp var)
(cond ((number? exp) 0)
((variable? exp) (if (same-variable? exp var) 1 0))
((sum? exp) (make-sum (deriv (addend exp) var)
(deriv (augend exp) var)))
((product? exp)
(make-sum
(make-product (multiplier exp)
(deriv (multiplicand exp) var))
(make-product (deriv (multiplier exp) var)
(multiplicand exp))))
(else
(error "unknown expression type: DERIV" exp))))
(define (variable? x) (symbol? x))
(define (same-variable? v1 v2)
(and (variable? v1) (variable? v2) (eq? v1 v2)))
(define (make-sum a1 a2) (list '+ a1 a2))
(define (make-product m1 m2) (list '* m1 m2))
(define (sum? x) (and (pair? x) (eq? (car x) '+)))
(define (addend s) (cadr s))
(define (augend s) (caddr s))
(define (product? x) (and (pair? x) (eq? (car x) '*)))
(define (multiplier p) (cadr p))
(define (multiplicand p) (caddr p)) so we could run the process:
> (deriv '(+ x 3) 'x) (+ 1 0) > (deriv '(* x y) 'x) (+ (* x 0) (* 1 y)) > (deriv '(* (* x y) (+ x 3)) 'x) (+ (* (* x y) (+ 1 0)) (* (+ (* x 0) (* 1 y)) (+ x 3)))but this process don’t known (* x 0) == 0, and (* 1 y) = y, or (+ 1 0) = 1. so we should simplify the make-sum and make-product:
(define (deriv exp var)
(cond ((number? exp) 0)
((variable? exp) (if (same-variable? exp var) 1 0))
((sum? exp) (make-sum (deriv (addend exp) var)
(deriv (augend exp) var)))
((product? exp)
(make-sum
(make-product (multiplier exp)
(deriv (multiplicand exp) var))
(make-product (deriv (multiplier exp) var)
(multiplicand exp))))
(else
(error "unknown expression type: DERIV" exp))))
(define (variable? x) (symbol? x))
(define (same-variable? v1 v2)
(and (variable? v1) (variable? v2) (eq? v1 v2)))
(define (=number? exp num) (and (number? exp) (= exp num)))
(define (make-sum a1 a2)
(cond ((=number? a1 0) a2)
((=number? a2 0) a1)
((and (number? a1) (number? a2))
(+ a1 a2))
(else (list '+ a1 a2))))
(define (make-product m1 m2)
(cond ((or (=number? m1 0) (=number? m2 0)) 0)
((=number? m1 1) m2)
((=number? m2 1) m1)
((and (number? m1) (number? m2)) (* m1 m2))
(else (list '* m1 m2))))
(define (sum? x) (and (pair? x) (eq? (car x) '+)))
(define (addend s) (cadr s))
(define (augend s) (caddr s))
(define (product? x) (and (pair? x) (eq? (car x) '*)))
(define (multiplier p) (cadr p))
(define (multiplicand p) (caddr p))
;1
(deriv '(+ x 3) 'x)
;y
(deriv '(* x y) 'x)
;(+ (* x y) (* y (+ x 3)))
(deriv '(* (* x y) (+ x 3)) 'x)
2.3.3 Example:Representing Sets
(define (element-of-set? x set)
(cond ((null? set) false)
((equal? x (car set)) true)
(else (element-of-set? x (cdr set))))) we could write
adjoin-set.If the object to be adjoined is already in the set, we just return the set. Otherwise, we use
cons to add the object to the list that represents the set:
(define (adjoin-set x set)
(if (element-of-set? x set)
set
(cons x set))) we could write
intersection-set using
element-of-set?:
(define (intersection-set set1 set2)
(cond ((or (null? set1) (null? set2)) '())
((element-of-set? (car set1) set2)
(cons (car set1) (intersection-set (cdr set1) set2)))
(else (intersection-set (cdr set1) set2))))
(define (element-of-set? x set)
(cond ((null? set) false)
((= x (car set)) true)
((< x (car set)) false)
(else (element-of-set? x (cdr set))))) and we could write
intersection-set in a faster way:
(define (intersection-set set1 set2)
(if (or (null? set1) (null? set2))
'()
(let ((x1 (car set1))
(x2 (car set2)))
(cond ((= x1 x2)
(cons x1 (intersection-set (cdr set1)
(cdr set2))))
((< x1 x2)
(intersection-set (cdr set1) set2))
((< x2 x1)
(intersection-set set1 (cdr set2)))))))

we could represent trees by using lists:
(define (entry tree) (car tree)) (define (left-branch tree) (cadr tree)) (define (right-branch tree) (caddr tree)) (define (make-tree entry left right) (list entry left right))now we can write the element-of-set? procedure:
(define (element-of-set? x set)
(cond ((null? set) false)
((= x (entry set)) true)
((< x (entry set))
(element-of-set? x (left-branch set)))
((> x (entry set))
(element-of-set? x (right-branch set))))) but how could we write
adjoin-set, to adjoin an item x, we compare x with the node entry to determine whether should be added to the right or to the left branch, and having adjoined x to the appropriate branch we piece this newly constructed branch together with the original entry and the other branch. If x is equal to the entry, we just return the node. If we are asked to adjoin x to an empty tree, we generate a tree that has x as the entry and empty right and left branches:
(define (adjoin-set x set)
(cond ((null? set) (make-tree x '() '()))
((= x (entry set)) set)
((< x (entry set))
(make-tree (entry set)
(adjoin-set x (left-branch set))
(right-branch set)))
((> x (entry set))
(make-tree (entry set)
(left-branch set)
(adjoin-set x (right-branch set)))))) but it is not a balance tree. we should use
B-tree and
red-black trees to generate a balance tree.
Sets and information retrieval
often, we could use sets to store the information that like ID in database. so if there have a lots records, we could write the process:
(define (lookup given-key set-of-records)
(cond ((null? set-of-records) false)
((equal? given-key (key (car set-of-records)))
(car set-of-records))
((< given-key (key (car set-of-records)))
(lookup given-key (left-branch set-of-records)))
((> given-key (key (car set-of-records)))
(lookup given-key (right-branch set-of-records)))))
2.3.4 Example:Huffman Encoding Trees
if we want to encode A~H, we should use 3 bits to encode that:
A 000 C 010 E 100 G 110 B 001 D 011 F 101 H 111with this code, the message:
BACADAEAFABBAAAGAHis encoded as the string of 54 bits:
we find that A is occurs frequent, so we could encode like that:
A 0 C 1010 E 1100 G 1110 B 100 D 1011 F 1101 H 1111with this code, the same message as above is encoded as the string of 42 bits:
but one of the difficulties of using a variable-length code is knowing when you have reached the end of a symbol in reading a sequence of zeros and ones. Morse code solves this problem by using a special separator code after the sequence of dots and dashes for each letter.Another solution is to design the code in such a way that no complete code for any symbol is the beginning of the code for another symbol. Such a code is called a prefix code.
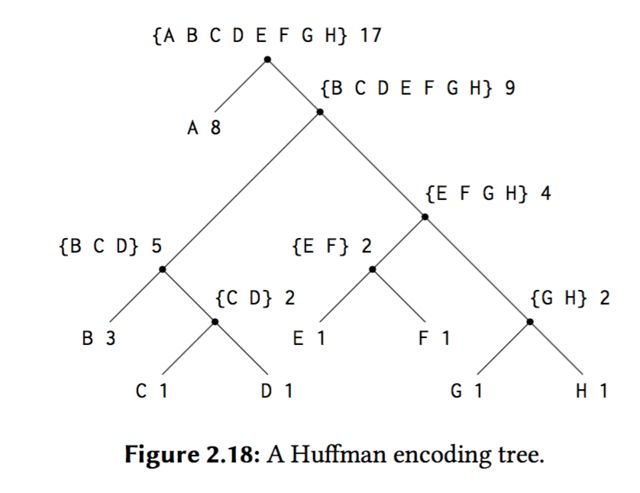
this is a Huffman tree:
The weights at the leaves indicate that the tree was designed for messages in which A appears with relative frequency 8, B with relative frequency 3, and the other letters each with relative frequency 1.
turn left is 0, and turn right is 1, so D is :1011, C is:1010.
Generating Huffman trees
The algorithm for generating a Huffman tree is very simple. The idea is to arrange the tree so that the symbols with the lowest frequency appear farthest away from the root.Begin with the set of leaf nodes, containing symbols and their frequencies, as determined by the initial data from which the code is to be constructed. Now find two leaves with the lowest weights and merge them to produce a node that has these two nodes as its left and right branches.The weight of the new node is the sum of the two weights. Remove the two leaves from the original set and replace them by this new node. Now continue this process.
Representing Huffman trees
leaves of the tree are represented by a list consisting of the symbol leaf, the symbol at the leaf, and the weight:
(define (make-leaf symbol weight) (list 'leaf symbol weight)) (define (leaf? object) (eq? (car object) 'leaf)) (define (symbol-leaf x) (cadr x)) (define (weight-leaf x) (caddr x))When we make a tree by merging two nodes, we obtain the weight of the tree as the sum of the weights of the nodes, and the set of symbols as the union of the sets of symbols for the nodes:
(define (make-code-tree left right)
(list left
right
(append (symbols left) (symbols right))
(+ (weight left) (weight right))))
(define (left-branch tree) (car tree))
(define (right-branch tree) (cadr tree))
(define (symbols tree)
(if (leaf? tree)
(list (symbol-left tree))
(caddr tree)))
(define (weight tree)
(if (leaf? tree)
(weight-leaf tree)
(cadddr tree)))
The decoding procedure
(define (decode bits tree)
(define (decode-1 bits current-branch)
(if (null? bits)
'()
(let ((next-branch
(choose-branch (car bits) current-branch)))
(if (leaf? next-branch)
(cons (symbol-leaf next-branch)
(decode-1 (cdr bits) tree))
(decode-1 (cdr bits) next-branch)))))
(decode-1 bits tree))
(define (choose-branch bit branch)
(cond ((= bit 0) (left-branch branch))
((= bit 1) (right-branch branch))
(else (error "bad bit:CHOOSE-BRANCH" bit))))
Sets of weighted elements
(define (adjoin-set x set)
(cond ((null? set) (list x))
((< (weight x) (weight (car set))) (cons x set))
(else (cons (car set)
(adjoin-set x (cdr set)))))) The following procedure takes a list of symbol-frequency pairs such as ((A 4) (B 2) (C 1) (D 1)) and constructs an initial ordered set of leaves, ready to be merged according to the Huffman algorithm.
(define (make-leaf-set pairs)
(if (null? pairs)
'()
(let ((pair (car pairs)))
(adjoin-set (make-leaf (car pair)
(cadr pair))
(make-leaf-set (cdr pairs))))))
2.4 Multiple Representations for Abstract Data
Data-abstraction barriers are powerful tools for controlling complexity.By isolating the underlying representations of data objects, we can divide the task of designing a large program into smaller tasks that can be performed separately.
2.4.1 Representations for Complex Numbers
two plausible representations for complex numbers:rectangular form(real part and imaginary part) and polar form(magnitude and angle).
from this picture, the complex number z = x + iy can be thought of as the point in the plane whose real coordinate is x and whose imaginary coordinate is y. so:
Real-part(z1 + z2) = Real-part(z1) + Real-part(z2)
Imaginary-part(z1 + z2) = Imaginary-part(z1) + Imaginary-part(z2)
when multiplying complex number, it is more natural to think in terms of representing a complex number in polar form:
Magnitude(z1 * z2) = Magnitude(z1) * Magnitude(z2)
Angle(z1 * z2) = Angle(z1) + Angle(z2)
so we should define six process: real-part, mag-part, magnitude, angle, and make-from-real-mag, make-from-mag-ang:
(define (add-complex z1 z2)
(make-from-real-imag (+ (real-part z1) (real-part z2))
(+ (imag-part z1) (imag-part z2))))
(define (sub-complex z1 z2)
(make-from-real-imag (- (real-part z1) (real-part z2))
(- (imag-part z1) (imag-part z2))))
(define (mul-complex z1 z2)
(make-from-mag-ang (* (magnitude z1) (magnitude z2))
(+ (angle z1) (angle z2))))
(define (div-complex z1 z2)
(make-from-mag-ang (/ (magnitude z1) (magnitude z2))
(- (angle z1) (angle z2)))) so there has two method to represent the process:
if we use x,y, we write the code:
(define (real-part z) (car z))
(define (imag-part z) (cdr z))
(define (magnitude z)
(sqrt (+ (square (real-part z))
(square (imag-part z)))))
(define (angle z)
(atan (imag-part z) (real-part z)))
(define (make-from-real-imag x y) (cons x y))
(define (make-from-mag-ang r a)
(cons (* r (cos a)) (* r (sin a)))) if we use r, A, we write the code:
(define (real-part z) (* (magnitude z) (cos (angle z))))
(define (imag-part z) (* (magnitude z) (sin (angle z))))
(define (magnitude z) (car z))
(define (angle z) (cdr z))
(define (make-from-real-imag x y)
(cons (sqrt (+ (square x) (square y)))
(atan y x)))
(define (make-from-mag-ang r a) (cons r a))
2.4.2 Tagged data
if we want to use real-imag or mag-ang, we should use type to identify them:
(define (attach-tag type-tag contents)
(cons type-tag contents))
(define (type-tag datum)
(if (pair? datum)
(car datum)
(error "Bad tagged datum: TYPE-TAG" datum)))
(define (contents datum)
(if (pair? datum)
(car datum)
(error "Bad tagged datum: CONTENTS" datum))) so we can identify that rectangular or polar:
(define (rectangular? z) (eq? (type-tag z) 'rectangular)) (define (polar? z) (eq? (type-tag z) 'polar))so the code should change:
(define (real-part-rectangular z) (car z))
(define (imag-part-rectangular z) (cdr z))
(define (magnitude-rectangular z)
(sqrt (+ (square (real-part-rectangular z))
(square (imag-part-rectangular z)))))
(define (angle-rectangular z)
(atan (imag-part-rectangular z) (real-part-rectangular z)))
(define (make-from-real-imag-rectangular x y)
(attach-tag 'rectangular (cons x y)))
(define (make-from-mag-ang-rectangular r a)
(attach-tag 'rectangular (cons (* r (cos a)) (* r (sin a)))))
(define (real-part-polar z) (* (magnitude-polar z) (cos (angle-polar z))))
(define (imag-part-polar z) (* (magnitude-polar z) (sin (angle-polar z))))
(define (magnitude-polar z) (car z))
(define (angle-polar z) (cdr z))
(define (make-from-real-imag-polar x y)
(attach-tag 'rectangular (cons (sqrt (+ (square x) (square y)))
(atan y x))))
(define (make-from-mag-ang-polar r a)
(attach-tag 'rectangular (cons r a))) so we now could define real-part, mag-part, magnitude and angle:
(define (real-part z)
(cond ((rectangular? z)
(real-part-rectangular (contents z)))
((polar? z)
(real-part-polar (contents z)))
(else (error "Unknown type:REAL-PART" z))))
(define (imag-part z)
(cond ((rectangular? z)
(imag-part-rectangular (contents z)))
((polar? z)
(imag-part-polar (content z)))
(else (error "Unknown type:IMAG-PART" z))))
(define (magnitude z)
(cond ((rectangular? z)
(magnitude-rectangular (contents z)))
((polar? z)
(magnitude-polar (contents z)))
(else (error "Unknown type:MAGNITUDE" z))))
(define (angle z)
(cond ((rectangular? z)
(angle-rectangular (contents z)))
((polar? z)
(angle-polar (contents z)))
(else (error "Unknown type:ANGLE" z)))) last, we define the make-from process:
(define (make-from-real-imag x y) (make-from-real-imag-rectangular x y)) (define (make-from-mag-ang r a) (make-from-mag-ang-polar r a))

2.4.3 Data-Directed Programming and Additivity
but dispatching on type has two significant weaknesses.
1: the generic interface procedures(real-part, imag-part, magnitude, and angle) must know about all the different representations.
2: even though the individual representations can be designed separately, we must guarantee that no two procedures in the entire system have the same name.
so we need data-directed programming:
Data-directed programming is the technique of designing programs to work with such a table directly.Previously, we implemented the mechanism that interfaces the complex-arithmetic code with the two representation packages as a set of procedures that each perform an explicit dispatch on type.
To implement this plan, assume that we have two procedures, put and get, for manipulating the operation-and-type table:
>(put <op> <type> <item>) installs the <item> in the table, indexed by the <op> and the <type>.
>(get <op> <type>) looks up the <op>, <type> entry in the table and returns the item found there. If no item is found, get returns false.
(define (install-rectangular-package)
;;internal procedures
(define (real-part z) (car z))
(define (imag-part z) (cdr z))
(define (make-from-real-imag x y) (cons x y))
(define (magnitude z)
(sqrt (+ (square (real-part z))
(square (imag-part z)))))
(define (angle z)
(atan (imag-part z) (real-part z)))
(define (make-from-mag-ang r a)
(cons (* r (cos a)) (* r (sin a))))
;;interface to the rest of the system
(define (tag x) (attach-tag 'rectangular x))
(put 'real-part '(rectangular) real-part)
(put 'imag-part '(rectangular) imag-part)
(put 'magnitude '(rectangular) manitude)
(put 'angle '(rectangular) angle)
(put 'make-from-real-imag 'rectangular
(lambda (x y) (tag (make-from-real-imag x y))))
(put 'make-from-mag-ang 'rectangular
(lambda (r a) (tag (make-from-mag-ang r a))))
'done)
(define (install-polar-package)
;;internal procedures
(define (magnitude z) (car z))
(define (angle z) (cdr z))
(define (make-from-mag-ang r a) (cons r a))
(define (real-part z) (* (magnitude z) (cos (angle z))))
(define (imag-part z) (* (magnitude z) (sin (angle z))))
(define (make-from-real-imag x y)
(cons (sqrt (+ (square x) (square y)))
(atan y x)))
;;interface to the rest of the system
(define (tag x) (attach-tag 'polar x))
(put 'real-part '(polar) real-part)
(put 'imag-part '(polar) imag-part)
(put 'magnitude '(polar) magnitude)
(put 'angle '(polar) angle)
(put 'make-from-real-imag 'polar
(lambda (x y) (tag (make-from-real-imag x y))))
(put 'make-from-mag-ang 'polar
(lambda (r a) (tag (make-from-mag-ang r a))))
'done) The complex-arithmetic selectors access the table by means of a general "operation" procedure called apply-generic:which applies a generic operation to some arguments.
(define (apply-generic op . args)
(let ((type-tags (map type-tag args)))
(let ((proc (get op type-tags)))
(if proc
(apply proc (map contents args))
(error
"No method for these types: APPLY-GENERIC"
(list op type-tags)))))) now we could define the process:
(define (real-part z) (apply-generic 'real-part z)) (define (imag-part z) (apply-generic 'imag-part z)) (define (magnitude z) (apply-generic 'magnitude z)) (define (angle z) (apply-generic 'angle z)) (define (make-from-real-imag x y) ((get 'make-from-real-imag 'rectangular) x y)) (define (make-from-mag-ang r a) ((get 'make-from-mag-ang 'polar) r a))
2.5 Systems with Generic Operations
now we shall build the structure:
2.5.1 Generic Arithmetic Operations
The generic arithmetic procedures are defined as follows:
(define (add x y) (apply-generic 'add x y)) (define (sub x y) (apply-generic 'sub x y)) (define (mul x y) (apply-generic 'mul x y)) (define (div x y) (apply-generic 'div x y))we will tag ordinary number with the symbol scheme-number.Since these operations each take two arguments, they are installed in the table keyed by the list(scheme-number, scheme-number):
(define (install-scheme-number-package)
(define (tag x) (attach-tag 'scheme-number x))
(put 'add '(scheme-number scheme-number)
(lambda (x y) (tag (+ x y))))
(put 'sub '(scheme-number scheme-number)
(lambda (x y) (tag (- x y))))
(put 'mul '(scheme-number scheme-number)
(lambda (x y) (tag (* x y))))
(put 'div '(scheme-number scheme-number)
(lambda (x y) (tag (/ x y))))
(put 'make 'scheme-number (lambda (x) (tag x)))
'done) Users of the Scheme-number package will create(tagged) ordinary numbers by means of the procedure:
(define (make-scheme-number n) ((get 'make 'scheme-number) n))
Now that we can readily include new kinds of numbers:
(define (install-rational-package)
;;internal procedures
(define (numer x) (car x))
(define (denom x) (cdr x))
(define (make-rat n d)
(let ((g (gcd n d)))
(cons (/ n g) (/ d g))))
(define (add-rat x y)
(make-rat (+ (* (numer x) (denom y))
(* (numer y) (denom x)))
(* (denom x) (denom y))))
(define (sub-rat x y)
(make-rat (- (* (numer x) (denom y))
(* (numer y) (denom x)))
(* (denom x) (denom y))))
(define (mul-rat x y)
(make-rat (* (numer x) (numer y))
(* (denom x) (denom y))))
(define (div-rat x y)
(make-rat (* (numer x) (denom y))
(* (denom x) (numer y))))
;;interface to rest of the system
(define (tag x) (attach-tag 'rational x))
(put 'add '(rational rational)
(lambda (x y) (tag (add-rat x y))))
(put 'sub '(rational rational)
(lambda (x y) (tag (sub-rat x y))))
(put 'mul '(rational rational)
(lambda (x y) (tag (mul-rat x y))))
(put 'div '(rational rational)
(lambda (x y) (tag (div-rat x y))))
(put 'make 'rational
(lambda (n d) (tag (make-rat n d))))
'done)
(define (make-rational n d)
((get 'make 'rational) n d)) we can install s similar package to handle complex numbers:
(define (install-complex-package)
;;imported procedures from rectangular and polar packages
(define (make-from-real-imag x y)
((get 'make-from-real-imag 'rectangular) x y))
(define (make-from-mag-ang r a)
((get 'make-from-mag-ang 'polar) r a))
;;internal procedures
(define (add-complex z1 z2)
(make-from-real-imag (+ (real-part z1) (real-part z2))
(+ (imag-part z1) (imag-part z2))))
(define (sub-complex z1 z2)
(make-from-real-imag (- (real-part z1) (real-part z2))
(- (imag-part z1) (imag-part z2))))
(define (mul-complex z1 z2)
(make-from-mag-ang (* (magnitude z1) (magnitude z2))
(+ (angle z1) (angle z2))))
(define (div-complex z1 z2)
(make-from-mag-ang (/ (magnitude z1) (magnitude z2))
(- (angle z1) (angle z2))))
;;interface to rest of the system
(define (tag z) (attach-tag 'complex z))
(put 'add '(complex complex)
(lambda (z1 z2) (tag (add-complex z1 z2))))
(put 'sub '(complex complex)
(lambda (z1 z2) (tag (sub-complex z1 z2))))
(put 'mul '(complex complex)
(lambda (z1 z2) (tag (mul-complex z1 z2))))
(put 'div '(complex complex)
(lambda (z1 z2) (tag (div-complex z1 z2))))
(put 'make-from-real-imag 'complex
(lambda (x y) (tag (make-from-real-imag x y))))
(put 'make-from-mag-ang 'complex
(lambda (r a) (tag (make-from-mag-ang r a))))
'done)
(define (make-complex-from-real-imag x y)
((get 'make-from-real-imag 'complex) x y))
(define (make-complex-from-mag-ang r a)
((get 'make-from-mag-ang 'complex) r a)) What we have here is a two-level tag system.A typical complex number, such as 3+4i in rectangular form, would be represented as show below:
2.5.2 Combining Data of Different Types
One way to handle cross-type operations is to design a different procedure for each possible combination of types for which the operation is valid.For example, we could extend the complex-number package so that it provides a procedure for adding complex numbers to ordinary numbers and installs this in the table using the tag:
(define (add-complex-to-schemenum z x)
(make-from-real-imag (+ (real-part z) x) (imag-part z)))
(put 'add '(complex scheme-number)
(lambda (z x) (tag (add-complex-to-schemenum z x)))) This technique works, but it is cumbersome.
Coercion
In general, we can implement this idea by designing coercion procedures that transform an object of one type into an equivalent object of another type.
(define (scheme-number->complex n)
(make-complex-from-real-imag (contents n) 0))
(put-coercion 'scheme-number
'complex
scheme-number->complex)