【C#算法实现】QQ小游戏天天连萌(连连看)算法。

算法是程序的灵魂，优秀的算法可以高效率解决实际问题。继腾讯安卓游戏天天爱消除之后又一款十分好玩的游戏——天天连萌，其实就是以前的连连看，在实现算法之前博主从来没有玩过这类游戏，只是看别人玩过，因此在实现之前必须清楚游戏的规则，必须注意许多细节，否则将严重影响算法的准确性，甚至实现了一个完全错误的算法。

游戏规则可以总结出来：

1.两相消元素必须是同种，这里的同种包括被赋予了某些特殊功能的元素。

2.相消元素之间的连线的直角拐角必须小于等于2个。

如图所示，红线相连的即可消除，灰线则不符合规则。

天天连萌是一个10*5的固定矩阵，每个不同元素可以简记为1,2,3,4...由于含有空白元素，这里约定空格记为0，因此上图中是这样一个数字化的矩阵：

1	0	1	0	2	1	0	3	0	4
0	5	0	0	4	6	0	0	7	0
5	2	7	0	0	0	0	8	2	5
0	8	0	0	4	5	0	0	6	0
4	0	8	0	2	3	0	1	0	8

现在要解决的问题的办法有两种：

1.直接查找，即取任意一个元素，向四个方向进行查找，0代表着"路"可以沿着"路"进行查找同种元素，遇到不同元素还要"拐弯"，三个方向，然后继续沿着0查找，只能拐两次弯。这种方法最容易想到，但是复杂度可想而知， 同时还要判断边界条件。

2.找两个相同元素，通过某种方法验证这两个是否可以相消。本文采用的是第二种方法，具体方法是对元素作扩展，这里的扩展是指包括自己在内的上下左右空白区域。再判断扩展区域是否可以连通。 

现在将该矩阵四周填充路径0，因为连线可以经过整个矩阵外围。

为了更好说明，将0用空白代替。

	1		1		2	1		3		4
		5			4	6			7
	5	2	7					8	2	5
		8			4	5			6
	4		8		2	3		1		8

任取两个相同元素，比如上面用蓝色标记的两个6，对两个点分别作水平扩展，如下图：

	1		1		2	1		3		4
		5			4	6	■		7
	5	2	7				||	8	2	5
		8			4	5	■		6
	4		8		2	3		1		8

再将扩展区域进行垂直投影，找出公共(重叠)部分，比如上图用黑框标注的单元格，再判断他们是否可以直线连通 ，如果可以直线连通那么这两个6就满足规则顺利消除(显然上图中的两个6可以消除 )。如果不能直线连通，那么再作垂直扩展：

			■	=	=	■
	1		1		2	1		3		4
		5			4	6			7
	5	2	7					8	2	5
		8			4	5			6
	4		8		2	3		1		8

如上图的两个1的垂直扩展区域可以直线连通，但水平扩展区域不能，满足两者之一即可消除。

实现代码如下：

将数据放进二维数组：

m_data = new int[5, 10]
{
    {1,0,1,0,2,1,0,3,0,4},
    {0,5,0,0,4,6,0,0,7,0},
    {5,2,7,0,0,0,0,8,2,5},
    {0,8,0,0,4,5,0,0,6,0},
    {4,0,8,0,2,3,0,1,0,8}
};

考虑到算法的时间复杂度，这里事先将所有相同元素的坐标放进动态数组。

这里采用ArrayList现成的动态数组进行存放坐标点

m_same = new ArrayList[10];//假定只有10种

            for (int x = 0; x < 5; ++x)
            {
                for (int y = 0; y < 10; ++y)
                {
                    int index = m_data[x, y];
                    if (m_same[index] == null)
                        m_same[index] = new ArrayList();
                    m_same[index].Add(new point(x, y));
                }
            }

下标代表种类，比如是0的格子放在m_same[0] 中，以此类推...

算法最重要的一步是计算扩展点位：

private void findEx(ref point pt, out ArrayList rowEx, out ArrayList colEx)
        {
            colEx = new ArrayList();
            colEx.Add(pt);
            //纵向
            int k = 1;
            int x = pt.m_x;
            int y = pt.m_y;
            bool flag1 = true, flag2 = true;//两个方向是否非空
            while (true)
            {
                //flag1->上 flag2->下
                //边界路径
                if (x - k == -1 || x + k == 5)
                {
                    if (x - k == -1 && flag1 != false)
                    {
                        colEx.Add(new point(x - k, y));
                        flag1 = false;
                    }
                    if (x + k == 5 && flag2 != false)
                    {
                        colEx.Add(new point(x + k, y));
                        flag2 = false;
                    }
                }
                if (x - k >= 0 && x - k <= 4 && flag1 != false)
                {
                    if (m_data[x - k, y] == 0)
                        colEx.Add(new point(x - k, y));
                    else
                        flag1 = false;
                }
                if (x + k >= 0 && x + k <= 4 && flag2 != false)
                {
                    if (m_data[x + k, y] == 0)
                        colEx.Add(new point(x + k, y));
                    else
                        flag2 = false;
                }
                if (!flag1 && !flag2)
                    break;
                k++;
            }
            //横向
            rowEx = new ArrayList();
            rowEx.Add(pt);
            k = 1;
            flag1 = true;
            flag2 = true;
            while (true)
            {
                //flag1->左 flag2->右
                //边界路径
                if (y - k == -1 || y + k == 10)
                {
                    if (y - k == -1 && flag1 != false)
                    {
                        rowEx.Add(new point(x, y - k));
                        flag1 = false;
                    }
                    if (y + k == 10 && flag2 != false)
                    {
                        rowEx.Add(new point(x, y + k));
                        flag2 = false;
                    }
                }
                if (y - k >= 0 && y - k <= 9 && flag1 != false)
                {
                    if (m_data[x, y - k] == 0)
                        rowEx.Add(new point(x, y - k));
                    else
                        flag1 = false;
                }
                if (y + k >= 0 && y + k <= 9 && flag2 != false)
                {
                    if (m_data[x, y + k] == 0)
                        rowEx.Add(new point(x, y + k));
                    else
                        flag2 = false;
                }
                if (!flag1 && !flag2)
                    break;

                k++;
            }
        }

为了简化代码，将竖直方向和水平方向的遍历通过一个k变量来作偏移，通过flag1,flag2标记是否到了"头".

下面将扩展点位进行连通判断：

private bool Available(ref point[] pt)
        {
            ArrayList[] rowEx, colEx;//建立横纵扩展位            
            rowEx = new ArrayList[2];
            colEx = new ArrayList[2];
            //分别计算两点的扩展位置(包括本身)
            findEx(ref pt[0],out rowEx[0],out colEx[0]);
            findEx(ref pt[1],out rowEx[1],out colEx[1]);

            //rowEx[]

            for (int i = 0; i < rowEx[0].Count; ++i)
            {
                for (int j = 0; j < rowEx[1].Count; ++j)
                {
                    int y1 = ((point)rowEx[0][i]).m_y;
                    int x1 = ((point)rowEx[0][i]).m_x;
                    int y2 = ((point)rowEx[1][j]).m_y;
                    int x2 = ((point)rowEx[1][j]).m_x;
                    if (y1 == y2)
                    {
                        bool flag = true;
                        //公共部分,检查是否连通
                        for (int k = Math.Min(x1, x2)+1; k < Math.Max(x1, x2); ++k)
                        {
                            if (y1 != -1 && y1 != 10 && m_data[k, y1] != 0)
                            {
                                flag = false;
                                break;
                            }
                        }
                        if (y1 == -1 || y1 == 10 || flag) return true;
                    }
                }
            }

            //colEx[]
            for (int i = 0; i < colEx[0].Count; ++i)
            {
                for (int j = 0; j < colEx[1].Count; ++j)
                {
                    int y1 = ((point)colEx[0][i]).m_y;
                    int x1 = ((point)colEx[0][i]).m_x;
                    int y2 = ((point)colEx[1][j]).m_y;
                    int x2 = ((point)colEx[1][j]).m_x;
                    if (x1 == x2)
                    {
                        bool flag = true;
                        //公共部分,检查是否连通
                        for (int k = Math.Min(y1, y2) + 1; k < Math.Max(y1, y2); ++k)
                        {
                            if (x1 != -1 && x1 != 5 && m_data[x1, k] != 0)
                            {
                                flag = false;
                                break;
                            }                            
                        }
                        if (x1 == -1 || x1 == 5 || flag) return true;
                    }
                }
            }

            return false;
        }

之后再将m_same中的元素求组合数，通过上面的函数进行验证就行了。

point[] pt = new point[2];

            for (int i = 1; i < m_same.GetLength(0); ++i)
            {//遍历ArrayList[]
                if (m_same[i] != null)
                {
                    for (int j = 0; j < m_same[i].Count - 1; ++j)
                    {//遍历相同元素集合
                        for (int k = j + 1; k < m_same[i].Count; ++k)
                        {//取组合数C(n,2)
                                pt[0] = (point)m_same[i][j];
                                pt[1] = (point)m_same[i][k];
                                if (Available(ref pt))
                                    m_results.Add(new point[2] { pt[0], pt[1] });
                                    //return pt;
                        }
                    }
                }
            }
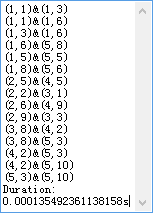
            return m_results;

实际运算结果如下图，这里采用了高精度计时器进行算法计时：