基于AR模型谱估计算法（Yule-Walker方法与Burg方法）的C++实现

头文件：

/*
 * Copyright (c) 2008-2011 Zhang Ming (M. Zhang), [email protected]
 *
 * This program is free software; you can redistribute it and/or modify it
 * under the terms of the GNU General Public License as published by the
 * Free Software Foundation, either version 2 or any later version.
 *
 * Redistribution and use in source and binary forms, with or without
 * modification, are permitted provided that the following conditions are met:
 *
 * 1. Redistributions of source code must retain the above copyright notice,
 *    this list of conditions and the following disclaimer.
 *
 * 2. Redistributions in binary form must reproduce the above copyright
 *    notice, this list of conditions and the following disclaimer in the
 *    documentation and/or other materials provided with the distribution.
 *
 * This program is distributed in the hope that it will be useful, but WITHOUT
 * ANY WARRANTY; without even the implied warranty of MERCHANTABILITY or
 * FITNESS FOR A PARTICULAR PURPOSE. See the GNU General Public License for
 * more details. A copy of the GNU General Public License is available at:
 * http://www.fsf.org/licensing/licenses
 */


/*****************************************************************************
 *                                  levinson.h
 *
 * If the coefficient matrix of a linear equations is Toeplitz, then it can
 * be solved in a high computational efficiency way through Levinson-Durbin
 * algorithm. The subroutiones in this file will be used for solving Wiener
 * -Hopf equeations in Wiener filtring and Yule- Walker equations in
 * parametric spectrum estimation, respectively.
 *
 * Zhang Ming, 2010-11, Xi'an Jiaotong University.
 *****************************************************************************/


#ifndef LEVINSON_H
#define LEVINSON_H


#include <vector.h>


namespace splab
{

    template<typename Type>
    Vector<Type> levinson( const Vector<Type>&, const Vector<Type>& );

    template<typename Type>
    Vector<Type> levinson( const Vector<Type>&, Type& );


    #include <levinson-impl.h>

}
// namespace splab


#endif
// LEVINSON_H

/*
 * Copyright (c) 2008-2011 Zhang Ming (M. Zhang), [email protected]
 *
 * This program is free software; you can redistribute it and/or modify it
 * under the terms of the GNU General Public License as published by the
 * Free Software Foundation, either version 2 or any later version.
 *
 * Redistribution and use in source and binary forms, with or without
 * modification, are permitted provided that the following conditions are met:
 *
 * 1. Redistributions of source code must retain the above copyright notice,
 *    this list of conditions and the following disclaimer.
 *
 * 2. Redistributions in binary form must reproduce the above copyright
 *    notice, this list of conditions and the following disclaimer in the
 *    documentation and/or other materials provided with the distribution.
 *
 * This program is distributed in the hope that it will be useful, but WITHOUT
 * ANY WARRANTY; without even the implied warranty of MERCHANTABILITY or
 * FITNESS FOR A PARTICULAR PURPOSE. See the GNU General Public License for
 * more details. A copy of the GNU General Public License is available at:
 * http://www.fsf.org/licensing/licenses
 */


/*****************************************************************************
 *                               parametricpse.h
 *
 * Parametric Power Spectrum Estimation Mothods.
 *
 * Techniques for spectrum estimation can generally be divided into parametric
 * (such as classical spectrum estimation) and non-parametric methods. The
 * parametric approaches assume that the underlying stationary stochastic
 * process has a certain structure which can be described using a small number
 * of parameters (for example, auto-regressive model). In these approaches,
 * the task is to estimate the parameters of the model that describes the
 * stochastic process.
 *
 * The widely used model is AR model, so this file provides three subroutines
 * to estimate the parameter of AR model, they are Yule-Walker method, Burg's
 * recursive mothod and forward-and-backward linear prediction least square
 * method.
 *
 * Zhang Ming, 2010-11, Xi'an Jiaotong University.
 *****************************************************************************/


#ifndef PARAMETRICPSE_H
#define PARAMETRICPSE_H


#include <vector.h>
#include <fft.h>
#include <correlation.h>
#include <levinson.h>
#include <linequs1.h>


namespace splab
{

    template<typename Type> Vector<Type> yulewalkerPSE( const Vector<Type>&,
                                                        int, Type& );
    template<typename Type> Vector<Type> burgPSE( const Vector<Type>&,
                                                  int, Type& );
    template<typename Type> Vector<Type> fblplsPSE( const Vector<Type>&,
                                                    int, Type& );

    template<typename Type> Vector<Type> armaPSD( const Vector<Type>&,
                                                  const Vector<Type>&,
                                                  const Type&, int );


    #include <parametricpse-impl.h>

}
// namespace splab


#endif
// PARAMETRICPSE_H

实现文件：

/*
 * Copyright (c) 2008-2011 Zhang Ming (M. Zhang), [email protected]
 *
 * This program is free software; you can redistribute it and/or modify it
 * under the terms of the GNU General Public License as published by the
 * Free Software Foundation, either version 2 or any later version.
 *
 * Redistribution and use in source and binary forms, with or without
 * modification, are permitted provided that the following conditions are met:
 *
 * 1. Redistributions of source code must retain the above copyright notice,
 *    this list of conditions and the following disclaimer.
 *
 * 2. Redistributions in binary form must reproduce the above copyright
 *    notice, this list of conditions and the following disclaimer in the
 *    documentation and/or other materials provided with the distribution.
 *
 * This program is distributed in the hope that it will be useful, but WITHOUT
 * ANY WARRANTY; without even the implied warranty of MERCHANTABILITY or
 * FITNESS FOR A PARTICULAR PURPOSE. See the GNU General Public License for
 * more details. A copy of the GNU General Public License is available at:
 * http://www.fsf.org/licensing/licenses
 */


/*****************************************************************************
 *                               levinson-impl.h
 *
 * Implementationfor Levinson-Durbin alogrithm.
 *
 * Zhang Ming, 2010-11, Xi'an Jiaotong University.
 *****************************************************************************/


/**
 * Levinson algorithm for solving Toeplitz equations.
 * t    : t(0), t(1), ..., t(n-1) of Toeplitz coefficient matrix
 * b    : constant vector
 */
template <typename Type>
Vector<Type> levinson( const Vector<Type> &t, const Vector<Type> &b )
{
    assert( t.size() == b.size() );

    int n = t.size();
	Type alpha, beta, q, c, omega;
	Vector<Type> y(n), yy(n), x(n);

	alpha = t[0];
	if( abs(alpha) < EPS )
	{
		cerr << "The matrix is ill-conditioned!" << endl;
		return x;
	}
	y[0] = 1;
	x[0] = b[0] / alpha;

	for( int k=1; k<n; ++k )
	{
		q = 0;
		beta = 0;
		for( int j=0; j<k; ++j )
		{
			q += x[j] * t[k-j];
			beta += y[j] * t[j+1];
		}
		c = -beta / alpha;

		yy[0] = c * y[k-1];
		y[k] = y[k-1];
		for( int i=1; i<k; ++i )
			yy[i] = y[i-1] + c*y[k-i-1];
		yy[k] = y[k-1];

		alpha += c*beta;
		if( abs(alpha) < EPS )
		{
			cerr << "The matrix is ill-conditioned!" << endl;
			return x;
		}

		omega = (b[k]-q) / alpha;
		for( int i=0; i<k; ++i )
		{
			x[i] += omega*yy[i];
			y[i] = yy[i];
		}
		x[k] = omega*y[k];
	}

	return x;
}


/**
 * Levinson-Durbin algorithm for solving Youle-Walker equations.
 * rn       : r(0), r(1), ..., r(p)
 * sigma2   : the variance of exciting white noise
 */
template <typename Type>
Vector<Type> levinson( const Vector<Type> &rn, Type &sigma2 )
{
    int p = rn.size()-1;
    Type tmp;
    Vector<Type> ak(p+1), akPrev(p+1);

    ak[0] = Type(1.0);
    sigma2 = rn[0];
    ak[1] = -rn[1]/sigma2;
    sigma2 *= 1 - ak[1]*ak[1];

    for( int k=2; k<=p; ++k )
    {
        tmp = 0;
        for( int i=0; i<k; ++i )
            tmp += ak[i]*rn[k-i];
        ak[k] = -tmp/sigma2;

        for( int i=1; i<k; ++i )
            akPrev[i] = ak[i] + ak[k]*ak[k-i];
        for( int i=1; i<k; ++i )
            ak[i] = akPrev[i];

        sigma2 *= 1 - ak[k]*ak[k];
    }

	return ak;
}

/*
 * Copyright (c) 2008-2011 Zhang Ming (M. Zhang), [email protected]
 *
 * This program is free software; you can redistribute it and/or modify it
 * under the terms of the GNU General Public License as published by the
 * Free Software Foundation, either version 2 or any later version.
 *
 * Redistribution and use in source and binary forms, with or without
 * modification, are permitted provided that the following conditions are met:
 *
 * 1. Redistributions of source code must retain the above copyright notice,
 *    this list of conditions and the following disclaimer.
 *
 * 2. Redistributions in binary form must reproduce the above copyright
 *    notice, this list of conditions and the following disclaimer in the
 *    documentation and/or other materials provided with the distribution.
 *
 * This program is distributed in the hope that it will be useful, but WITHOUT
 * ANY WARRANTY; without even the implied warranty of MERCHANTABILITY or
 * FITNESS FOR A PARTICULAR PURPOSE. See the GNU General Public License for
 * more details. A copy of the GNU General Public License is available at:
 * http://www.fsf.org/licensing/licenses
 */


/*****************************************************************************
 *                            parametricpse-impl.h
 *
 * Implementation for parametric power spectrum estimatoin methods.
 *
 * Zhang Ming, 2010-11, Xi'an Jiaotong University.
 *****************************************************************************/


/**
 * The Yule-Walker method for AR power spectral estimation.
 * xn       : input signal
 * p        : the AR model order
 * sigma2   : the variance of exciting white noise
 * return   : coefficients of AR model --- a(0), a(1), ..., a(p)
 */
template <typename Type>
Vector<Type> yulewalkerPSE( const Vector<Type> &xn, int p, Type &sigma2 )
{
    int N = xn.size();

    assert( p <= N );

    Vector<Type> rn(p+1);
    for( int i=0; i<=p; ++i )
        for( int k=0; k<N-i; ++k )
            rn[i] += xn[k+i]*xn[k];
    rn /= Type(N);

    return levinson( rn, sigma2 );
}


/**
 * The Burg method for AR power spectral estimation.
 * xn       : input signal
 * p        : the AR model order
 * sigma2   : the variance of exciting white noise
 * return   : coefficients of AR model --- a(0), a(1), ..., a(p)
 */
template <typename Type>
Vector<Type> burgPSE( const Vector<Type> &xn, int p, Type &sigma2 )
{
    int N = xn.size();
    Type numerator, denominator;
    Vector<Type> ak(p+1), akPrev(p+1), ef(N), eb(N);

    ak[0] = Type(1.0);
    sigma2 = sum(xn*xn) / Type(N);

    for( int i=1; i<N; ++i )
    {
        ef[i] = xn[i];
        eb[i-1] = xn[i-1];
    }

    for( int k=1; k<=p; ++k )
    {
        numerator = 0;
        denominator = 0;
        for( int i=k; i<N; ++i )
        {
            numerator += ef[i]*eb[i-1];
            denominator += ef[i]*ef[i] + eb[i-1]*eb[i-1];
        }
        ak[k] = -2*numerator/denominator;

        for( int i=1; i<k; ++i )
            akPrev[i] = ak[i] + ak[k]*ak[k-i];
        for( int i=1; i<k; ++i )
            ak[i] = akPrev[i];

        sigma2 *= 1 - ak[k]*ak[k];

        for( int i=N-1; i>k; --i )
        {
            ef[i] = ef[i] + ak[k]*eb[i-1];
            eb[i-1] = eb[i-2] + ak[k]*ef[i-1];
        }
    }

    return ak;
}


/**
 * Forward and backward linear prediction least square method for
 * AR power spectral estimation.
 * xn       : input signal
 * p        : the AR model order
 * sigma2   : the variance of exciting white noise
 * return   : coefficients of AR model --- a(0), a(1), ..., a(p)
 */
template <typename Type>
Vector<Type> fblplsPSE( const Vector<Type> &xn, int p, Type &sigma2 )
{
    int N = xn.size(),
        M = 2*(N-p);

    Vector<Type> u(p+1);
    u[0] = Type(1.0);

    Matrix<Type> X(M,p+1);
//    for( int i=0; i<=p; ++i )
//    {
//        for( int j=0; j<N-p; ++j )
//            X[j][i] = xn[i+j];
//        for( int j=p; j<N; ++j )
//            X[j][i] = xn[j-i];
//    }
    for( int i=0; i<N-p; ++i )
        for( int j=0; j<=p; ++j )
            X[i][j] = xn[i+j];
    for( int i=p; i<N; ++i )
        for( int j=0; j<=p; ++j )
            X[i][j] = xn[i-j];

    Matrix<Type> Rp = trMult(X,X) / Type(M);
    Vector<Type> ak = luSolver( Rp, u );
    sigma2 = 1/ak[0];
    ak *= sigma2;

    return ak;
}


/**
 * The Bartlett method of power spectral estimation.
 * ak       : AR coefficients
 * bk       : MA coefficients
 * sigma2   : the variance of exciting white noise
 * L        : the points number of PSD
 * return   : spectral density at L frequencies:
 *            w = 0, 2*pi/L, ..., 2*pi(L-1)/L
 */
template <typename Type>
Vector<Type> armaPSD( const Vector<Type> &ak, const Vector<Type> &bk,
                      const Type &sigma2, int L )
{
    int p = ak.size()-1,
        q = bk.size()-1;
    Vector<Type> Xk(L);

    Type zRe, zIm, aRe, aIm, bRe, bIm,
         Xre, Xim,
         re, im;
	Type omega,
         den, numRe, numIm;

	for( int k=0; k<L; ++k )
	{
		omega = Type(TWOPI*k/L);
		zRe = cos(-omega);
		zIm = sin(-omega);

        // numerator
		bRe = 0;
		bIm = 0;
		for( int i=q; i>0; --i )
		{
			re = bRe;
			im = bIm;
			bRe = (re+bk[i])*zRe - im*zIm;
			bIm = (re+bk[i])*zIm + im*zRe;
		}
		bRe += bk[0];

        // denominator
		aRe = 0;
		aIm = 0;
		for( int i=p; i>0; --i )
		{
			re = aRe;
			im = aIm;
			aRe = (re+ak[i])*zRe - im*zIm;
			aIm = (re+ak[i])*zIm + im*zRe;
		}
		aRe += ak[0];

        // Power Spectrum Density
		numRe = aRe*bRe + aIm*bIm;
		numIm = aRe*bIm - aIm*bRe;
		den = aRe*aRe + aIm*aIm;
		Xre = numRe/(den);
		Xim = numIm/(den);
        Xk[k] = sigma2 * (Xre*Xre + Xim*Xim);
	}

	return Xk;
}

测试代码：

/*****************************************************************************
 *                            parametricpse_test.cpp
 *
 * parametric power spectrum estimation testing.
 *
 * Zhang Ming, 2010-11, Xi'an Jiaotong University.
 *****************************************************************************/


#define BOUNDS_CHECK

#include <iostream>
#include <iomanip>
#include <cstring>
#include <random.h>
#include <vectormath.h>
#include <parametricpse.h>
#include "engine.h"


using namespace std;
using namespace splab;


typedef double  Type;
const   int     N = 50;
const   int     L = 200;
const   int     yuleOrder = 4;
const   int     burgOrder = 4;
const   int     lplsOrder = 4;


int main()
{
    /******************************* [ signal ] ******************************/
    cout << setiosflags(ios::fixed) << setprecision(4);
    int mfn = L/2+1;
    Type amp1 = Type(1.0),
         amp2 = Type(1.0);
    Type f1 = Type(0.2),
         f2 = Type(0.4);
    Type sigma2, SNR;

    Vector<Type> tn = linspace(Type(0), Type(N-1), N );
    Vector<Type> sn = amp1*sin(TWOPI*f1*tn) + amp2*sin(TWOPI*f2*tn);
    Vector<Type> wn = randn( 37, Type(0.0), Type(0.1), N );
    Vector<Type> xn = sn + wn;
    SNR = 20*log10(norm(sn)/norm(wn));
    cout << "The SNR = " << SNR << endl << endl;

    /********************************* [ PSD ] *******************************/
//    Vector<Type> ak = yulewalkerPSE( xn, yuleOrder, sigma2 );
//    cout << "The estimated AR coefficients by Youle-Walker method are: "
//         << ak << endl;

//    Vector<Type> ak = burgPSE( xn, burgOrder, sigma2 );
//    cout << "The estimated AR coefficients by Burg method are: "
//         << ak << endl;

    Vector<Type> ak = fblplsPSE( xn, lplsOrder, sigma2 );
    cout << "The estimated AR coefficients by Youle-Walker method are: "
         << ak << endl;

    cout << "The estimated variance is:   " << sigma2 << endl << endl;

    Vector<Type> bk(1,Type(1.0));
    Vector<Type> Px = armaPSD( ak, bk, sigma2, L );

    /******************************** [ PLOT ] *******************************/
	Engine *ep  = engOpen( NULL );
	if( !ep )
	{
		cerr << "Cannot open Matlab Engine!" << endl;
		exit(1);
	}

	mxArray *mxn = mxCreateDoubleMatrix( N, 1, mxREAL );
    mxArray *mPx = mxCreateDoubleMatrix( mfn, 1, mxREAL );
	memcpy( mxGetPr(mxn), xn, N*sizeof(Type) );
	memcpy( mxGetPr(mPx), Px, mfn*sizeof(Type) );
	engPutVariable( ep, "xn", mxn );
	engPutVariable( ep, "Px", mPx );

	const char *mCmd =  " figure('name','FBLPLS Method of Spectrum Estimation'); \
        N = length(xn); mfn = length(Px); \
        subplot(2,1,1); \
            plot((0:N-1), xn); \
            axis([0,N,min(xn),max(xn)]); \
            title('(a)   Signal', 'FontSize',12); \
            xlabel('Samples', 'FontSize',12); \
            ylabel('Amplitude', 'FontSize',12); \
        subplot(2,1,2); \
            h = stem((0:mfn-1)/(mfn-1)/2, Px); \
            axis([0,0.5,min(Px),max(Px)]); \
            set(h,'MarkerFaceColor','blue'); \
            set(gca, 'XTick', 0:0.1:0.5); \
            grid on; \
            title('(b)   Spectrum', 'FontSize',12); \
            xlabel('Normalized Frequency ( f / fs )', 'FontSize',12); \
            ylabel('Amplitude', 'FontSize',12); ";
    engEvalString( ep, mCmd );

	mxDestroyArray( mxn );
	mxDestroyArray( mPx );
    system( "pause" );
	engClose(ep);

	return 0;
}

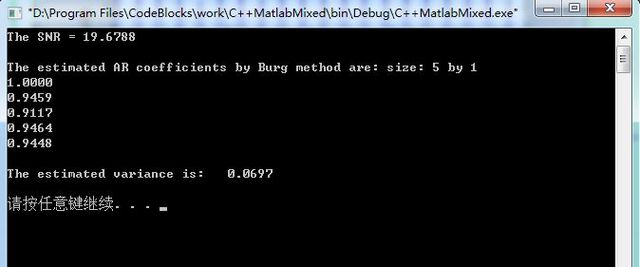
运行结果：