R语言 - 6 R图形基础
本章讨论的所有内容可以按以下的思路来说:图形化定性或者说描述性变量(柱状图、脊柱图、饼图及扇形图),图形化定量型变量(直方图及核密度图),图形化变量的发散趋势(箱图)以及在单一轴上刻画大量数据的方法-点图。
柱状图- Bar Plot
柱状图的主要作用是以水平条或垂直条的方式显示Categorical变量的分布(频数)。R提供了barplot() 函数来支持柱状图的创建,其最简单的形式如下:barplot(height)。其中height是向量或矩阵,如果是向量的话显示如左,矩阵则会描绘一个堆积柱状图(beside=FALSE)或组柱状图(beside=TRUE):

【提示】如果Categorical变量是factor或有序factor,那么直接用plot函数产生跟barplot一样的效果
下面的代码创建了一个比较全的柱状图:
barplot (m, main="Sales byRegion",col=c("red","green","grey","blue"),xlab="region",ylab="Sales")

spine()函数产生类似于SSRS中百分百堆积柱状图:
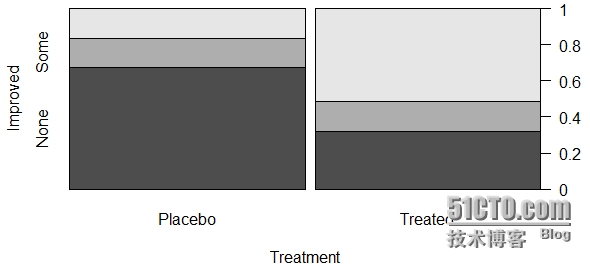
饼图
除了柱状图/条形图外,饼图是另外一种经常用来刻画Categorical类型变量的分布的图形。虽然柱状图比较流行但是很多统计学家包括本书的作者都不推荐使用饼图,而是推荐使用柱状图或点图,因为对于人来说判断长度比判断面积更准确容易。饼图使用下面的函数创建:
pie(x, labels)
x是一个非负的数值向量来指示饼图每个切片的大小,lables是一个字符向量指示每个切片的标签。
饼图有个问题,人们很难比较饼图中不同的切片之间的大小,除非每个切片上都有数值标签,所以有了下面的扇图:

直方图
直方图用来显示连续性变量的分布情况,它将连续性的数据在x轴上切分成一段一段的小格子,并在Y轴上为每个小格子显示频率。R使用下面的函数创建直方图:
hist(x,freq=TRUE/FALSE, breaks=value, col=”red”, xlab=”annotation in x axis”,main=”title of the hist”)
其中x是一个连续性的数值向量,如果freq为TRUE表示基于频数创建的直方图,否则表示基于频率创建直方图;breaks会指示直方图会在X轴上创建几个小盒子:

另外在执行完hist函数描绘了一个直方图之后,我们可以再调用其他绘图函数(比如lines)来将一条线加在直方图上,如上有图所示即将数据集的核密度估计(KDE)描绘了出来:
核密度图
核密度估计是一种评估连续性随机变量的的概率密度函数的有效方法。我们前面已经看过使用直方图的形式表述一个连续性随机变量的概率密度函数,核密度估计以一种更平滑的方式来描述概率密度。其函数形式为
density(x)
下图是使用plot(density(mtcars$mpg))来展示mtcars中mpg变量的核密度估计。本例子直接用plot来描画,plot会创建一个新的图形,如果是要往已经存在的图形上附加的话要使用lines()函数:
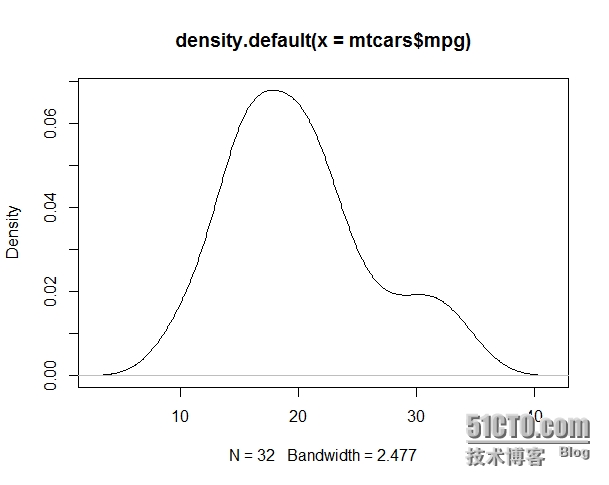
核密度估计另一个重要的作用是可以在不同的分组间比较某变量的概率分布,sm包的sm.density.compare()函数提供了这种功能。下面的函数及图形就是以cyl分组查看mpg的概率密度函数:
sm.density.compare(mpg, cyl, xlab="Miles PerGallon")

Box画图
箱图通过图形化某个连续性变量的5个特征量(最小值、第一四分位、中位数、第三四分位和最大值)来描述该变量的分布,初次之外它还有可能显示离群点(在正负1.5倍IQR之外的数)。
例如boxplot(mtcars$mpg)会显示下面的箱图。我们可以使用boxplot.stats(mtcars$mpg)来打印5个特征量的值。

正如我们在核密度图中看到的分组比较,使用箱图在不同组之间做比较。其函数形式为:boxplot(formula,data=dataframe),其中data指定箱图所基于的数据帧对象,formula是形如y~A的公式,y指箱图所描述的变量,A是指基于该列(或多列A*B)分组变量y来做箱图。下图以cyl分组mpg做箱图:boxplot(mpg~cyl,data=mtcars)。从中我们可以看到6缸的车的mpg数据更对称一些:

点图
http://lectures.molgen.mpg.de/Pairwise/DotPlots/index.html
点图提供了一种方式在一个简单的水平轴上描画大量的有标签的数值,R提供了dotchart()函数来实现这种能力,其最简单的调用方式是:
dotchart(x, labels=)
其中x是数值向量,labels是一个字符向量指示了每个数值的标签。下图是我们使用dotchart(mpg,labels=row.names(mtcars),cex=0.7)所创建的点图:

除了上面简单的形式意外,点图更有意思的一种表现形式是,我们可以首先排序然后使用groups选项指示各个点以某个因子变量分组,如下图所示:
