Scala程序集 N皇后问题
N皇后问题是由8皇后问题推广而来的
八皇后问题是一个以国际象棋为背景的问题:如何能够在8×8的国际象棋棋盘上放置八个皇后,使得任何一个皇后都无法直接吃掉其他的皇后?为了达到此目的,任两个皇后都不能处于同一条横行、纵行或斜线上。
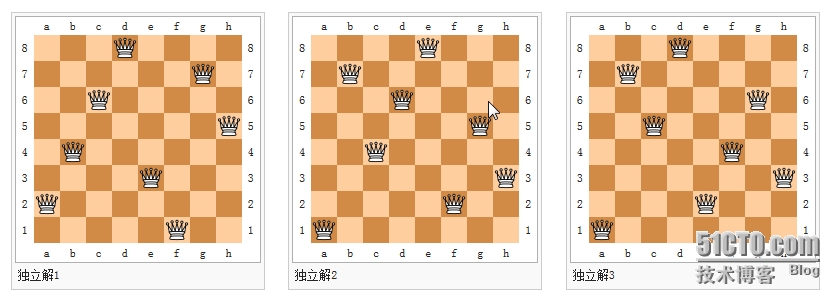
八皇后问题共有92个解, 上图便是其中3个解
解这个问题的Scala程序
package puzzles
/**
* Created by Bo on 2015/1/1.
*/
package object queen {
def isSafe(column: Int, queens: List[Int], delta: Int): Boolean = {
def abs(z: Int) = if (z > 0) z else -z
queens match {
case Nil => true
case x::xs => (column != x) && (abs(column - x) != delta) && isSafe(column, xs, delta+1)
}
}
def queens(n: Int): List[List[Int]] = {
def placeQueen(k: Int): List[List[Int]] = {
if (k == 0) List(List())
else for {
queens <- placeQueen(k-1) // k is the row number of current placement
column <- List.range(1, n+1) // why n+1 ? because there is n columns
if (isSafe(column, queens, 1))} yield column :: queens
}
placeQueen(n)
}
}
测试程序
package puzzles.queen
/**
* Created by Bo on 2015/1/1.
*/
object Test extends App{
val solutions = queens(8)
printf("Found %d solution(s)\n", solutions.length)
for (s <- solutions) println(s)
}
/*
Found 92 solution(s)
List(4, 2, 7, 3, 6, 8, 5, 1)
List(5, 2, 4, 7, 3, 8, 6, 1)
List(3, 5, 2, 8, 6, 4, 7, 1)
List(3, 6, 4, 2, 8, 5, 7, 1)
List(5, 7, 1, 3, 8, 6, 4, 2)
List(4, 6, 8, 3, 1, 7, 5, 2)
List(3, 6, 8, 1, 4, 7, 5, 2)
List(5, 3, 8, 4, 7, 1, 6, 2)
List(5, 7, 4, 1, 3, 8, 6, 2)
List(4, 1, 5, 8, 6, 3, 7, 2)
List(3, 6, 4, 1, 8, 5, 7, 2)
List(4, 7, 5, 3, 1, 6, 8, 2)
List(6, 4, 2, 8, 5, 7, 1, 3)
List(6, 4, 7, 1, 8, 2, 5, 3)
List(1, 7, 4, 6, 8, 2, 5, 3)
List(6, 8, 2, 4, 1, 7, 5, 3)
List(6, 2, 7, 1, 4, 8, 5, 3)
List(4, 7, 1, 8, 5, 2, 6, 3)
List(5, 8, 4, 1, 7, 2, 6, 3)
List(4, 8, 1, 5, 7, 2, 6, 3)
List(2, 7, 5, 8, 1, 4, 6, 3)
List(1, 7, 5, 8, 2, 4, 6, 3)
List(2, 5, 7, 4, 1, 8, 6, 3)
List(4, 2, 7, 5, 1, 8, 6, 3)
List(5, 7, 1, 4, 2, 8, 6, 3)
List(6, 4, 1, 5, 8, 2, 7, 3)
List(5, 1, 4, 6, 8, 2, 7, 3)
List(5, 2, 6, 1, 7, 4, 8, 3)
List(6, 3, 7, 2, 8, 5, 1, 4)
List(2, 7, 3, 6, 8, 5, 1, 4)
List(7, 3, 1, 6, 8, 5, 2, 4)
List(5, 1, 8, 6, 3, 7, 2, 4)
List(1, 5, 8, 6, 3, 7, 2, 4)
List(3, 6, 8, 1, 5, 7, 2, 4)
List(6, 3, 1, 7, 5, 8, 2, 4)
List(7, 5, 3, 1, 6, 8, 2, 4)
List(7, 3, 8, 2, 5, 1, 6, 4)
List(5, 3, 1, 7, 2, 8, 6, 4)
List(2, 5, 7, 1, 3, 8, 6, 4)
List(3, 6, 2, 5, 8, 1, 7, 4)
List(6, 1, 5, 2, 8, 3, 7, 4)
List(8, 3, 1, 6, 2, 5, 7, 4)
List(2, 8, 6, 1, 3, 5, 7, 4)
List(5, 7, 2, 6, 3, 1, 8, 4)
List(3, 6, 2, 7, 5, 1, 8, 4)
List(6, 2, 7, 1, 3, 5, 8, 4)
List(3, 7, 2, 8, 6, 4, 1, 5)
List(6, 3, 7, 2, 4, 8, 1, 5)
List(4, 2, 7, 3, 6, 8, 1, 5)
List(7, 1, 3, 8, 6, 4, 2, 5)
List(1, 6, 8, 3, 7, 4, 2, 5)
List(3, 8, 4, 7, 1, 6, 2, 5)
List(6, 3, 7, 4, 1, 8, 2, 5)
List(7, 4, 2, 8, 6, 1, 3, 5)
List(4, 6, 8, 2, 7, 1, 3, 5)
List(2, 6, 1, 7, 4, 8, 3, 5)
List(2, 4, 6, 8, 3, 1, 7, 5)
List(3, 6, 8, 2, 4, 1, 7, 5)
List(6, 3, 1, 8, 4, 2, 7, 5)
List(8, 4, 1, 3, 6, 2, 7, 5)
List(4, 8, 1, 3, 6, 2, 7, 5)
List(2, 6, 8, 3, 1, 4, 7, 5)
List(7, 2, 6, 3, 1, 4, 8, 5)
List(3, 6, 2, 7, 1, 4, 8, 5)
List(4, 7, 3, 8, 2, 5, 1, 6)
List(4, 8, 5, 3, 1, 7, 2, 6)
List(3, 5, 8, 4, 1, 7, 2, 6)
List(4, 2, 8, 5, 7, 1, 3, 6)
List(5, 7, 2, 4, 8, 1, 3, 6)
List(7, 4, 2, 5, 8, 1, 3, 6)
List(8, 2, 4, 1, 7, 5, 3, 6)
List(7, 2, 4, 1, 8, 5, 3, 6)
List(5, 1, 8, 4, 2, 7, 3, 6)
List(4, 1, 5, 8, 2, 7, 3, 6)
List(5, 2, 8, 1, 4, 7, 3, 6)
List(3, 7, 2, 8, 5, 1, 4, 6)
List(3, 1, 7, 5, 8, 2, 4, 6)
List(8, 2, 5, 3, 1, 7, 4, 6)
List(3, 5, 2, 8, 1, 7, 4, 6)
List(3, 5, 7, 1, 4, 2, 8, 6)
List(5, 2, 4, 6, 8, 3, 1, 7)
List(6, 3, 5, 8, 1, 4, 2, 7)
List(5, 8, 4, 1, 3, 6, 2, 7)
List(4, 2, 5, 8, 6, 1, 3, 7)
List(4, 6, 1, 5, 2, 8, 3, 7)
List(6, 3, 1, 8, 5, 2, 4, 7)
List(5, 3, 1, 6, 8, 2, 4, 7)
List(4, 2, 8, 6, 1, 3, 5, 7)
List(6, 3, 5, 7, 1, 4, 2, 8)
List(6, 4, 7, 1, 3, 5, 2, 8)
List(4, 7, 5, 2, 6, 1, 3, 8)
List(5, 7, 2, 6, 3, 1, 4, 8)
*/