深度学习:RBM理论与C++实战
时间过得真快啊,深度学习已经火的快十年了,不过目前,仍有人继续观望,也有些观望者“忍不住”陆续加入了这个逐渐庞大的研究团体,开始相信“深度”的power了。这不,前些日子Duke大学的副校长Lawrence Carin就过来介绍他们团队的研究成果,谈了谈他对深度学习的理解,并且开始相信这种深层结构的有效性。
我也谈谈对深度学习的理解吧,才疏学浅,不正确的地方请多多指教。深度学习表达的是一种概念,而非某一种具体的算法。它在某个方面是受到了神经生物学研究成果的启发,主要是Hubel和Wiesel(1959-1962)发现视觉皮质是分层次的,换句话说,视觉系统是分层处理其接收到的信息的。自此人们开始模拟这种分层的信息处理系统,如风靡一时的BP,Autoencoder,CNNs,SparseCoding等。直到2006年Hinton提出DBNs(Deep Belief Networks)和DBMs(Deep Boltzmann Machines,这里指AutoEncoder Stacks这种框架)后,深度学习这个名词才被提出。DBNs和DBMs的训练主要分为两部分,pretraining和finetuning。pretraing中采用分层训练的方法,这样不仅降低了训练时间也防止出现过拟合。每层网络训练中,有一个输入层(也叫可见层),也就是系统接收到的信息,有一个特征层(也叫隐含层),也就是系统对接收到的信息的处理结果(特征表达)。每层的网络结构实际上是一个生成模型RBM(Restricted Boltzmann Machine),为了防止深层模型过拟合,要保证每层网络结构中的输入层到特征层的响应再次生成到输入层后要尽可能的与原输入层相似,并以此准则为优化目标去调整层网络结构的参数。训练完一层后,再将该层的特征层作为下一层网络结构的输入层继续以同样的准则训练下一层网络。在pretraining阶段训练(unsupervised)得到的这个深层网络的参数实际上是比较接近模型的最优参数,此时再通过BP进行深层模型的参数调优是比较合理的,并有效的防止了过拟合。在这里值得一提的是,正是因为在finetuning阶段DBNs需要样本的类别,这就决定了DBNs和DBMs是不同的模型,DBNs是生成模型(generative model),而DBMs是判别模型(discriminative model)。生成模型认为观察值(类比于DBNs中的输入层)是由状态(类比于样本观察值的类别)生成的,它不像判别模型直接对P(状态|观察值)建模,而是考虑联合概率P(状态,观察值),也就是还考虑了P(观察值|状态);而判别模型直接对P(状态|观察值)建模。在finetuning阶段,对于DBNs模型参数的调优就是让调整后的参数使得P(观察值|状态)最大,因此其是一个生成模型;而对于DBMs模型,由于其是一个对称模型,对于模型参数的调优仍是在让P(状态|观察值)最大,因此其是判别模型。
鉴于DBNs和DBMs模型是深度学习中的两种主要算法框架,本文旨在介绍构成这两种模型的基本结构RBM模型的理论,并给出其程序实现。这里推荐一篇论文,张春霞的《受限制玻尔兹曼机简介》,对于想自己实现RBM的小伙伴来说是非常实用的资料,内容不仅丰富而且简单易懂,当然Hinton的论文也是要看的哈,毕竟人家是鼻祖。接下来的理论部分就来自该论文再加上自己的一些理解。后续看情况也会对DBNs和DBMs框架的理论及实现进行分析,源代码也不难找到的,Github上,Hinton的主页上都可以下载的哈。
1. RBM理论
1)RBM的基本模型
RBM的基本模型可用下图描述(为了讨论方便,定义模型中所有结点的取值只能是0和1,当然其也可以是0到1的实数):
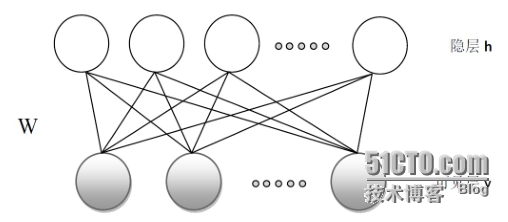
对于给定的一组状态(v,h)是RBM系统的能量定义为:
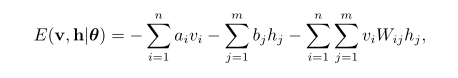
其中Wij表示可见单元i与隐单元j之间的连接权重,ai表示可见单元i的偏置,bj表示隐单元j的偏置。当参数确定时,基于该能量函数我们可以得到(v,h)的联合概率分布:

对于一个实际问题,我们最关心的是由RBM所定义的关于观测数据v的分布P(v|θ),即联合概率分布P(v,h|θ)的边际分布:

为了计算该分布,我们需要计算Z(θ)(归一化因子,也叫配分函数, partition function)。但对于一个可见层有n个结点,隐含层有m个结点的RBM来说,计算Z(θ)需要2^n * 2^m次,这使得不能有效的计算Z(θ)。
但是,由于RBM是层间有连接,层内无连接的,于是当给定可见单元的状态时,各隐单元之间是条件独立的。此时,可以使用sigmoid函数来作为隐单元的概率响应,于是有:
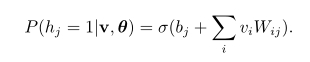
其中,σ(x)为sigmoid激活函数。
由于RBM的结构是对称的,当给定隐单元的状态时,各可见单元的激活状态之间也是条件独立的,即第i个可见单元的激活概率为:
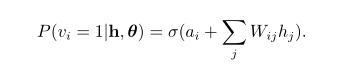
2)RBM模型参数的学习
对RBM模型参数θ的学习的准则如下:
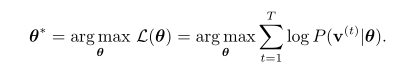
这个准则通俗一点描述就是,输入层到特征层的响应再次生成到输入层后要尽可能的与原输入层相似。
为了获得最优的θ,可以使用随机梯度上升法(stochastic gradient ascent)求L(θ)的最大值。其中,求L(θ)的梯度的推导如下:

其中《。》P表示求关于分布P的数学期望。上式中的第一项容易求出,而第二项由于Z(θ)的存在,一般采用近似计算的方法,如Gibbs采样。
分别用data和model表示P(h|v(t), θ)和P(v,h|θ),于是L(θ)的梯度可由如下式子来表示:

3)Gibbs采样

通俗一点说,要求一个可见层n个结点及隐含层m个结点的RBM模型的Z(θ)需要2^n * 2^m次,如果n和m很大的话,那么Z的计算就变得不可行,于是我们把该RBM模型所有可能出现的状态(2^n * 2^m种)看做是一个总体,对它进行采样,用采样得到的样本去估计总体。上面的k步采样中的k实际上是远比2^n * 2^m小的,这样对Z进行估计计算的话就变得可行了。
4)基于对比散度的RBM快速学习算法
2002年Hinton提出了一个RBM的快速学习算法,对比散度(contrastive divergence,CD)。与吉布斯采样不同Hinton指出当使用训练数据初始化v0时,我们仅需要使用k(通常k=1)步吉布斯采样便可以得到足够好的近似。在CD算法一开始,可见单元的状态被设置成一个训练样本,并利用式
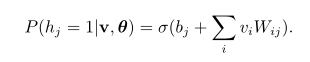
计算所有隐层单元的二值状态。在所有隐层单元的状态确定之后,根据式
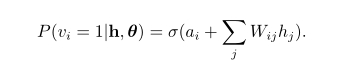
来确定第i个可见单元vi取值为1的概率,进而产生可见层的一个重构(reconstruction)。这样,在使用随机梯度上升法最大化L(θ)在训练数据上的值时,各参数的更新准则为:
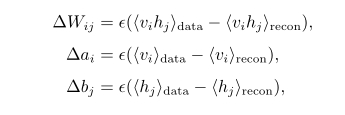
这里,e是学习率,也就是按梯度方向更新参数的速度,《。》recon表示一步重构后模型定义的分布。CD算法描述如下:

2. RBM的C++实现
由于个人比较偏向于使用C++语言,所以一般对于感兴趣的算法都会选择C++语言去实现。这里分享一个算法实现过程的经验,一般在算法实现过程中,首先我会考虑找其源代码,如果别人已经实现了,我就会对他的代码进行评价,比如说最重要的代码层次是否清晰,层次清晰是很重要的,要知道整个计算机系统在搭建的过程中我们考虑最多的问题就是分层,哪些由硬件做,哪些由软件做。算法实现也一样,对于算法的核心部分最好不要依赖于特定的库,不是说不可以,这样做是考虑到可移植性。而在基于核心算法的应用中需要与用户进行交互,这里就可以依赖于特定的库了,方便我们快速的完成应用系统的实现。如果对现有的代码比较满意的话,直接拿来用就好了,如果不满意,可以自己写(有些代码看着看着就想自己写了,哈哈),或者改现有的代码。
下面列出来的这个代码是Github上的一个开源的对Hinton的Matlab版本的一个C++实现,个人比较喜欢C++的这个版本,层次清晰,稍微的改动了几个个人觉得不好的部分和给出较为详细的注释。Matlab版本可以到Hinton的主页下载:
http://www.cs.toronto.edu/~hinton/MatlabForSciencePaper.html,
C++版本地址:https://github.com/jdeng/rbm-mnist。
下面给出代码:
#include <iostream>
#include <numeric>
#include <vector>
#include <random>
#include <memory>
#include <fstream>
#include <chrono>
#include <functional>
/*
Note:: it is better not to extend the standard vectors, because they
do not have virtual functions.
*/
/**
* @brief definitions about some basic operations that could
* be used for training a RBM
*/
typedef std::vector<float> ivector;
namespace v {
struct LightVector
{
std::pair<float *, float *> pair_;
LightVector() {}
LightVector(float* begin, float* end) {
pair_ = std::pair<float*, float*>(begin, end);
}
LightVector(const LightVector& bh) {
pair_ = bh.pair_;
}
float *data() const { return pair_.first; }
size_t size() const { return std::distance(pair_.first, pair_.second); }
bool empty() const { return pair_.first == pair_.second; }
float& operator[](size_t i) { return *(pair_.first + i); }
float operator[](size_t i) const { return *(pair_.first + i); }
};
template <class Vector1, class Vector2> inline float dot(const Vector1&x, const Vector2& y) {
int m = x.size(); const float *xd = x.data(), *yd = y.data();
float sum = 0.0;
while (--m >= 0) sum += (*xd++) * (*yd++);
return sum;
}
// saxpy: x = x + g * y; x = a * x + g * y
inline void saxpy(ivector& x, float g, const ivector& y) {
int m = x.size(); float *xd = x.data(); const float *yd = y.data();
while (--m >= 0) (*xd++) += g * (*yd++);
}
inline void saxpy(float a, ivector& x, float g, const ivector& y) {
int m = x.size(); float *xd = x.data(); const float *yd = y.data();
while (--m >= 0) { (*xd) = a * (*xd) + g * (*yd); ++xd; ++yd; }
}
inline void saxpy2(ivector& x, float g, const ivector& y, float h, const ivector& z) {
int m = x.size(); float *xd = x.data(); const float *yd = y.data(); const float *zd = z.data();
while (--m >= 0) { (*xd++) += (g * (*yd++) + h * (*zd++)); }
}
inline void scale(ivector& x, float g) {
int m = x.size(); float *xd = x.data();
while (--m >= 0) (*xd++) *= g;
}
#if 0
inline void addsub(ivector& x, const ivector& y, const ivector& z) {
int m = x.size(); float *xd = x.data(); const float *yd = y.data(); const float *zd = z.data();
while (--m >= 0) (*xd++) += ((*yd++) - (*zd++));
}
#endif
inline void unit(ivector& x) {
float len = ::sqrt(dot(x, x));
if (len == 0) return;
int m = x.size(); float *xd = x.data();
while (--m >= 0) (*xd++) /= len;
}
inline bool isfinite(const ivector& x) {
for(auto const& i: x) { if (! _finite(i)) return false; } //std::isfinite(i)
return true;
}
}
/**
* @brief Batch is a struct used for training, during which all samples
* are deviede into several batchs and each batch keeps its begin and
* end
*
* @param pair_ keep each batch's begin and end iterator
*
*/
struct Batch
{
typedef std::vector<ivector>::iterator Iterator;
std::pair<Iterator, Iterator> pair_;
Batch() {
}
Batch(Iterator begin, Iterator end) {
pair_ = std::pair<Iterator, Iterator>(begin, end);
}
Batch(const Batch& bh) {
pair_ = bh.pair_;
}
Iterator begin() const { return pair_.first; }
Iterator end() const { return pair_.second; }
size_t size() const { return std::distance(pair_.first, pair_.second); }
bool empty() const { return pair_.first == pair_.second; }
ivector& operator[](size_t i) { return *(pair_.first + i); }
const ivector& operator[](size_t i) const { return *(pair_.first + i); }
};
/**
* @brief RBMType an enum for hidden layer's active function,
* struct RBMConf keeps configuration for each RBM's training,
* struct RBM represents a RBM
*/
enum class RBMType
{
SIGMOID,
LINEAR,
EXP
};
struct RBMConf
{
float momentum_, weight_cost_, learning_rate_;
RBMConf(float momentum=0.5, float weight_cost=0.0002, float learning_rate=0.1):
momentum_(momentum), weight_cost_(weight_cost), learning_rate_(learning_rate) {
}
RBMConf(const RBMConf& conf) {
momentum_=conf.momentum_;
weight_cost_=conf.weight_cost_;
learning_rate_=conf.learning_rate_;
}
};
struct RBM
{
/**
* @brief what is inside RBM
*
*/
ivector bias_visible_, bias_hidden_, bias_visible_inc_, bias_hidden_inc_;
ivector weight_, weight_inc_;
RBMType type_;
RBMConf conf_;
static float sigmoid(float x) { return (1.0 / (1.0 + exp(-x))); }
static const ivector& bernoulli(const ivector& input, ivector& output)
{
static std::default_random_engine eng(::time(NULL));
static std::uniform_real_distribution<float> rng(0.0, 1.0);
for (size_t i=0; i<input.size(); ++i) { output[i] = (rng(eng) < input[i])? 1.0 : 0.0; }
return output;
}
static const ivector& add_noise(const ivector& input, ivector& output)
{
static std::default_random_engine eng(::time(NULL));
static std::normal_distribution<float> rng(0.0, 1.0);
for (size_t i=0; i<input.size(); ++i) { output[i] = input[i] + rng(eng); }
return output;
}
RBM() {}
/**
* @brief RBM constructor
*
* @param visible number of nodes for visible layer
* @param hidden number of nodes for hidden layer
* @param type of active function for hidden nodes
* @param conf configuration for traing a RBM
*/
RBM(size_t visible, size_t hidden, RBMType type = RBMType::SIGMOID, RBMConf& conf = RBMConf())
: bias_visible_(visible), bias_hidden_(hidden), weight_(visible * hidden)
, bias_visible_inc_(visible), bias_hidden_inc_(hidden), weight_inc_(visible * hidden)
, type_(type), conf_(conf)
{
static std::default_random_engine eng(::time(NULL));
static std::normal_distribution<float> rng(0.0, 1.0);
for (auto& x: weight_) x = rng(eng) * .1;
}
/**
* @brief get size of RBM
*/
size_t num_hidden() const { return bias_hidden_.size(); }
size_t num_visible() const { return bias_visible_.size(); }
size_t num_weight() const { return weight_.size(); }
/**
* @brief copy a RBM to another
*/
int mirror(const RBM& rbm)
{
size_t n_visible = bias_visible_.size(), n_hidden = bias_hidden_.size();
if (n_hidden != rbm.num_visible() || n_visible != rbm.num_hidden()) {
std::cout << "not mirrorable" << std::endl;
return -1;
}
bias_visible_ = rbm.bias_hidden_;
bias_hidden_ = rbm.bias_visible_;
for (size_t i = 0; i < n_visible; ++i) {
for (size_t j = 0; j < n_hidden; ++j) {
weight_[j * n_visible + i] = rbm.weight_[i * n_hidden + j];
}
}
return 0;
}
/**
* @brief activate the hidden layer's nodes according to RBM's Type
*
* @param visibel for visible layer's nodes
* @param hidden for hidden layer's nodes
* @param bias_hidden for hidden nodes' bias
* @param weight for corresponding weights between visible nodes and hidden nodes
*
* @return hidden layer's nodes
*/
const ivector& activate_hidden(const ivector& visible, ivector& hidden) const {
size_t n_visible = visible.size(), n_hidden = hidden.size();
std::fill(hidden.begin(), hidden.end(), 0);
for (size_t i = 0; i < n_hidden; ++i) {
float *xd = const_cast<float *>(weight_.data() + i * n_visible);
float s = v::dot(visible, v::LightVector(xd, xd + n_visible));
s += bias_hidden_[i];
if (type_ == RBMType::SIGMOID) s = sigmoid(s);
else if (type_ == RBMType::EXP) s = exp(s);
hidden[i] = s;
}
return hidden;
}
template <class Vector1, class Vector2, class Vector3>
static const Vector2& activate_hidden(const Vector1& visible, Vector2& hidden, const Vector3& bias_hidden, const Vector3& weight, RBMType type)
{
size_t n_visible = visible.size(), n_hidden = hidden.size();
std::fill(hidden.begin(), hidden.end(), 0);
for (size_t i = 0; i < n_hidden; ++i) {
float *xd = const_cast<float *>(weight.data() + i * n_visible);
float s = v::dot(visible, v::LightVector(xd, xd + n_visible));
s += bias_hidden[i];
if (type == RBMType::SIGMOID) s = sigmoid(s);
else if (type == RBMType::EXP) s = exp(s);
hidden[i] = s;
}
return hidden;
}
/**
* @brief activate the hidden layer's nodes using sigmoid
*
* @param hidden for hidden layer's nodes
* @param visible for visible layer's nodes
*
* @return visible nodes
*/
const ivector& activate_visible(const ivector& hidden, ivector& visible) const
{
size_t n_visible = bias_visible_.size(), n_hidden = bias_hidden_.size();
std::fill(visible.begin(), visible.end(), 0);
for (size_t i = 0; i < n_visible; ++i) {
float s = 0;
for (size_t j = 0; j < n_hidden; ++j) s += hidden[j] * weight_[j * n_visible+ i];
s += bias_visible_[i];
s = sigmoid(s);
visible[i] = s;
}
return visible;
}
/**
* @brief train the RBM
*
* @param inputs for training samples
*
* @return training error
*/
float train(Batch& inputs)
{
size_t n_visible = bias_visible_.size(), n_hidden = bias_hidden_.size();
float momentum = conf_.momentum_, learning_rate = conf_.learning_rate_, weight_cost = conf_.weight_cost_;
// temporary results
ivector v1(n_visible), h1(n_hidden), v2(n_visible), h2(n_hidden), hs(n_hidden);
//delta
ivector gw(n_visible * n_hidden), gv(n_visible), gh(n_hidden);
for (auto const& input: inputs) {//C++11 serial iterateration,
//inputs could be a vector or an object of a class
//in which functions begin() and end() are defined
//with a iterator type return.
v1 = input;
this->activate_hidden(v1, h1);
this->activate_visible((type_ == RBMType::LINEAR? add_noise(h1, hs): bernoulli(h1, hs)), v2);
this->activate_hidden(v2, h2);
for (size_t i = 0; i < n_visible; ++i) {
for (size_t j = 0; j < n_hidden; ++j) gw[j * n_visible + i] += h1[j] * v1[i] - h2[j] * v2[i];
}
// gh += (h1 - h2);
// gv += (v1 - v2);
v::saxpy2(gh, 1.0, h1, -1.0, h2);
v::saxpy2(gv, 1.0, v1, -1.0, v2);
}
//update
size_t n_samples = inputs.size();
// gw /= float(n_samples);
// gw -= weight_ * weight_cost;
v::saxpy(1.0/n_samples, gw, -weight_cost, weight_);
// weight_inc_ = weight_inc_ * momentum + gw * learning_rate;
v::saxpy(momentum, weight_inc_, learning_rate, gw);
// weight_ += weight_inc_;
v::saxpy(weight_, 1.0, weight_inc_);
// gh /= float(n_samples);
// bias_hidden_inc_ = bias_hidden_inc_ * momentum + gh * learning_rate;
v::saxpy(momentum, bias_hidden_inc_, learning_rate / n_samples, gh);
// bias_hidden_ += bias_hidden_inc_;
v::saxpy(bias_hidden_, 1.0, bias_hidden_inc_);
// gv /= float(n_samples);
// bias_visible_inc_ = bias_visible_inc_ * momentum + gv * learning_rate;
v::saxpy(momentum, bias_visible_inc_, learning_rate / n_samples, gv);
// bias_visible_ += bias_visible_inc_;
v::saxpy(bias_visible_, 1.0, bias_visible_inc_);
// float error = sqrt(gv.dot(gv) / n_visible);
v::scale(gv, 1.0/n_samples);
float error = sqrt(v::dot(gv, gv) / n_visible);
return error;
}
virtual float free_energy() const
{
size_t n_visible = bias_visible_.size(), n_hidden = bias_hidden_.size();
float s = 0;
for (size_t i = 0; i < n_visible; ++i) {
for (size_t j = 0; j < n_hidden; ++j)
s += weight_[j * n_visible+ i] * bias_hidden_[j] * bias_visible_[i];
}
return -s;
}
template <typename T> static void _write(std::ostream& os, const T& v) { os.write(reinterpret_cast<const char *>(&v), sizeof(v)); }
void store(std::ostream& os) const
{
int type = (int)type_;
size_t n_visible = bias_visible_.size();
size_t n_hidden = bias_hidden_.size();
_write(os, type); _write(os, n_visible); _write(os, n_hidden);
for (float v: bias_visible_) _write(os, v);
for (float v: bias_hidden_) _write(os, v);
for (float v: weight_) _write(os, v);
}
template <typename T> static void _read(std::istream& is, T& v) { is.read(reinterpret_cast<char *>(&v), sizeof(v)); }
void load(std::istream& is)
{
int type = 0;
size_t n_visible = 0, n_hidden = 0;
_read(is, type); _read(is, n_visible); _read(is, n_hidden);
type_ = (RBMType)type;
bias_visible_.resize(n_visible);
bias_hidden_.resize(n_hidden);
weight_.resize(n_visible * n_hidden);
for (float& v: bias_visible_) _read(is, v);
for (float& v: bias_hidden_) _read(is, v);
for (float& v: weight_) _read(is, v);
}
};
本文出自 “Remys” 博客,谢绝转载!