迪杰斯特拉算法(C语言实现)
迪杰斯特拉算法(C语言实现)
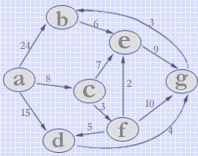
如上图,求以a为源点到个顶点的最短路劲。
#include "stdio.h"
#include "stdlib.h"
//用一个最大数表示顶点之间不相关
#define MAX 999
//设置顶点个数
#define MAX_VERTEX_NUM 7
//表示顶点之间不关联的常量
int INFINITY = MAX;
//记录顶点是否被访问过,已访问值为1,未访问值为0
int final[MAX_VERTEX_NUM];
//从指定顶点到其他各个节点的最短路径
int dist[MAX_VERTEX_NUM];
//记录路径
char path[MAX_VERTEX_NUM][MAX_VERTEX_NUM];
//实现构造图的矩阵关系,在图初始化的时候赋值到G.arcs[][]中
int temp[MAX_VERTEX_NUM][MAX_VERTEX_NUM]={
{ 0, 24, 8, 15,MAX,MAX,MAX},
{MAX, 0,MAX,MAX, 6,MAX,MAX},
{MAX,MAX, 0,MAX, 7, 3,MAX},
{MAX,MAX,MAX, 0,MAX,MAX, 4},
{MAX,MAX,MAX,MAX, 0,MAX, 9},
{MAX,MAX,MAX, 5, 2, 0, 10},
{MAX, 3,MAX,MAX,MAX,MAX, 0}
};
//图中顶点关系的二维数组表示
typedef struct ArcCell{
int adj;
char *info;
}AdjMatrix[MAX_VERTEX_NUM][MAX_VERTEX_NUM];
//图的结构体,vexs顶点的一维数组
//AdjMatrix类型的关系矩阵,vexnum为顶点个数,arcnum为关系个数。
typedef struct{
char vexs[MAX_VERTEX_NUM];
AdjMatrix arcs;
int vexnum;
int arcnum;
}MGraph;
//初始化图,依次初始化顶点为abc...
//然后把实现已构造temp[][]矩阵赋值到图的G.arcs[][]矩阵关系中
MGraph initMGraph(MGraph G)
{
int i,j;
char char_a='a';
//依次构建顶点为a,b,c...
for(i=0;i<MAX_VERTEX_NUM;i++)
{
G.vexs[i]=(char)((int)char_a+i);
printf("%c ",G.vexs[i]);
}
printf("\n");
//G.arcs[][]=temp[][]
for(i=0;i<MAX_VERTEX_NUM;i++)
{
for(j=0;j<MAX_VERTEX_NUM;j++)
{
G.arcs[i][j].adj=temp[i][j];
printf("%3d ",G.arcs[i][j].adj);
}
printf("\n");
}
G.vexnum=7;
G.arcnum=12;
return G;
}
//判定指定顶点到各顶点中路径最小的
//需要去除已经访问的顶点final[i]!=1再做最小路径比较
//返回下标
int mininum(int* dist)
{
int i,min=MAX,min_i;
for(i=0;i<MAX_VERTEX_NUM;i++)
{
if(dist[i]!=0&&dist[i]<min&&final[i]!=1)
{
min=dist[i];
min_i=i;
}
}
if(min==MAX)
return -1;
return min_i;
}
//顶点是否在图中
int exist_v(MGraph G,char u)
{
int i,s=-1;
for(i=0;i<G.vexnum;i++)
if(G.vexs[i]==u)
s=i;
if(s==-1)
return 0;
return 1;
}
//图最小路径算法
void ShortestPath_DIJ(MGraph G,char u)
{
int s=-1,i,j,k,min_i,path_p,count,c;
char v;
//查找源点的下标,用s记录
for(i=0;i<G.vexnum;i++)
if(G.vexs[i]==u)
s=i;
for(i=0;i<G.vexnum;i++)
{
final[i]=0;
dist[i]=G.arcs[s][i].adj;
v=G.vexs[i];
if(dist[i]<INFINITY&&dist[i]!=0)
{
path[i][0]=u;
path[i][1]=v;
printf("init path%d=%c-%c-\n",i,path[i][0],path[i][1]);
}
}
//初始化从源点到源点的路径为0,把源点设置为已访问(也就是把源点加入到S中)
dist[s]=0;
final[s]=1;
for(i=1;i<G.vexnum;i++)
{
min_i=mininum(dist);
printf("\nmin_i=%d ",min_i);
printf("\tvisited index---");
for(c=0;c<G.vexnum;c++)
if(final[c]==1)
printf("%d ",c);
//当前中间点与图中任何顶点都不关联
if(min_i==-1)
break;
final[min_i]=1;
//更新其他顶点最短路径
for(k=0;k<G.vexnum;k++)
{
if(G.arcs[min_i][k].adj!=0)
{
//更新路劲值,路径表示(如a-b-c)
if((dist[min_i]+G.arcs[min_i][k].adj)<dist[k])
{
dist[k]=dist[min_i]+G.arcs[min_i][k].adj;
for(path_p=0;path[min_i][path_p]!=0;path_p++)
path[k][path_p]=path[min_i][path_p];
path[k][path_p]=G.vexs[k];
}
}
}
//输出执行一次后的dist[]最短路径情况
printf("\n----------------------------------------------------\n");
for(count=0;count<G.vexnum;count++)
{
if(dist[count]==MAX)
printf("\tMAX");
else
printf("\t%3d ",dist[count]);
}
}
//输出路径表示
printf("\n---------the--------------path----------------------");
for(count=0;count<G.vexnum;count++)
{
printf("\npath%d=",count);
for(j=0;j<G.vexnum;j++)
if(path[count][j]&&path[count][j]!=path[count][j-1])
printf("%c-",path[count][j]);
}
}
int main(void)
{
int i,j;
char v;
MGraph G;
//初始化图
G=initMGraph(G);
//计算最短路径
v='a';
if(exist_v(G,v))
ShortestPath_DIJ(G,v);
else
printf("the vertex %c has no path",v);
system("pause");
return 0;
}
本文出自 “给力” 博客,谢绝转载!