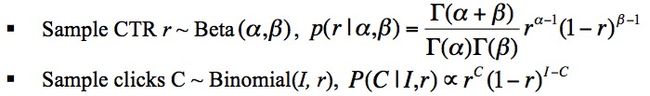广告计算——平滑CTR
一、广告计算的基本概念
1、广告的形式
在互联网发展的过程中,广告成为了互联网企业盈利的一个很重要的部分,根据不同的广告形式,互联网广告可以分为:
- 展示广告(display ads)
- 赞助商搜索广告(sponsored search)
- 上下文广告(contextual advertising)
2、竞价模型
对于在线广告,主要有如下的几种竞价模型:
- 按展示付费(pay-per-impression):直观来讲,按展示付费是指广告商按照广告被展示的次数付费,这是一种最普遍的竞价模型;
- 按行为付费(pay-per-action):按行为付费是指只有在广告产生了销售或者类似的一些转化时,广告商才付费;
当然,对于以上的两种竞价模型各有其局限性:在按展示付费模型中,压根没有考虑到广告的效果,只是按照广告流量进行售卖的模式;对于按行为付费模型,虽然其考虑到了广告效果,但其的条件是产生了某种转化,这种转化有时很难追踪和记录。此时,为了解决这两种模型的局限性,通常可以按照一个用户是否会点击广告作为最终的度量标准,即按点击付费模型(pay-per-click)。
- 按点击付费(pay-per-click):根据用户是否会点击广告来付费。
这里便出现了一个重要的概念,便是广告点击率(the click-through rate, CTR)。
3、广告点击率(CTR)
广告点击率CTR是度量一个用户对于一个广告的行为的最好的度量方法,广告点击率可以定义为:对于一个广告的被点击(click)的次数于被展示(impression)的次数的比值。
广告点击率对于在线广告有着重要的作用,在网络中,对于有限的流量,通常要选择出最优质的广告进行投放,此时,CTR可以作为选择广告和确定广告顺序的一个重要的标准。
但是在计算CTR时,由于数据的稀疏性,利用上述的计算方法得到的CTR通常具有较大的偏差,这样的偏差主要表现在如下的两种情况:
- 1、例如展示impression的次数很小,如1次,其中,点击的次数也很小(这里的很小是指数值很小),如1,按照上述的CTR的计算方法,其CTR为1,此时的点击率就被我们估计高了;
- 2、例如展示的次数很大,但是点击的次数很小,此时,利用上述的方法求得的CTR就会比实际的CTR要小得多。
出现上述两种现象的主要原因是我们对分子impression和分母click的估计不准确引起的,部分原因可能是曝光不足等等,对于这样的问题,我们可以通过相关的一些广告的展示和点击数据对CTR的公式进行平滑处理。
二、CTR的平滑方法
1、数据的层次结构——贝叶斯平滑
假设有N个相同的账号(a1,a2,⋯,aN),对于网页p,对于这样的网页和账号组(p,ai)。假设(C1,C2,⋯,CN)为观测到点击数据,(r1,r2,⋯,rN)为隐含的CTR的值,为点击率,点击率在此是一个隐含的参数,广告是否被点击满足二项分布,即Binomial(Ii,ri),其中,Ii表示广告被展示的次数。
贝叶斯思想认为,隐含的参数不是一个具体的值,而是满足某个分布,我们知道贝叶斯参数估计的基本过程为:
先验分布+数据的知识=后验分布
已知二项分布的共轭分布为Beta分布,对此,有以下的两点假设:
- 1、对于一个广告,其点击Ci符合二项分布Binomial(Ii,ri),其中,Ii表示的是展示的次数,ri表示的是广告被点击的概率;
- 2、对于所有的广告,有其自身的CTR,其CTR满足参数是α和β的贝塔分布Beta(α,β)。
假设有N个广告,广告被展示的次数为(I1,I2,⋯,IN),广告被点击的次数为(C1,C2,⋯,CN),上述的两个假设可以表示为如下的形式:
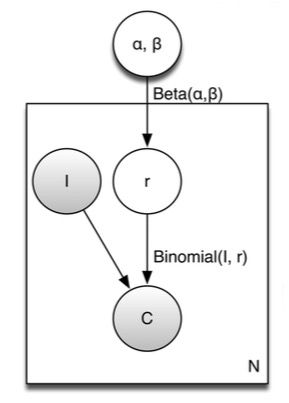
其对应的概率图模型为:
点击率ri不仅与(Ii,Ci)相关,而且与参数α和参数β相关,我们可以通过计算得到参数α和参数β的估计α̂ 和β̂ ,一旦α̂ 和β̂ 被确定后,则ri的估计为:
所以,现在,我们需要求解参数α和参数β的估计α̂ 和β̂ 。
点击C的似然函数为:ℙ(C1,C2,⋯,CN∣I1,I2,⋯,IN,α,β),由于点击的次数以及展示的次数之间都是相互独立的,因此上式可以表示为:
已知
则上式可以写成:
此时,我们需要求得该似然函数的最大值,首先,我们对上述的似然函数取对数,即为:
将上述的log似然函数分别对α和β求导数,即为:
其中,Ψ(x)=ddxlnΓ(x)。通过 the fixed-point iteration方法,可以得到如下的结果:
上述的求解过程是一个迭代的过程,一旦求出了参数α和参数β的估计α̂ 和β̂ ,便可以求出点击率的估计:
2、数据在时间上的一致性——指数平滑
相比上述的贝叶斯平滑,指数平滑相对要简单点,对于CTR中的点击,这是个与时间相关的量,假设对于一个广告,有M天的点击和展示数据(I1,I2,⋯,IM),(C1,C2,⋯,CM)。若要估计第M天的CTR的值,我们需要对分别对I和C进行平滑,得到平滑后的Î 和Ĉ 。其计算方法如下:
其中,γ称为平滑因子,且0<γ<1。对于上述的公式,若要计算第M天的平滑点击,可以得到下面的公式:
参考文献
- Click-Through Rate Estimation for Rare Events in Online Advertising.Xuerui Wang, Wei Li, Ying Cui, Ruofei (Bruce) Zhang, Jianchang Mao Yahoo! Labs, Silicon Valley United States