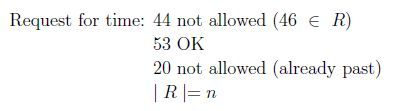MIT Introduction to Algorithms 学习笔记(六)
Lecture 5: Scheduling and Binary Search Trees
1. 跑道预留系统( Runway Reservation System)
Airport with single (very busy) runway.
“Reservations" for future landings.
When plane lands, it is removed from set of pending events.
Reserve req specify "requested landing time" t.
Add t to the set if no other landings are scheduled within k minutes either way. Assume that k can vary.
- else error, don't schedule
Example:
飞机预留的降落时间 R = (41, 46,49,56),K = 3.
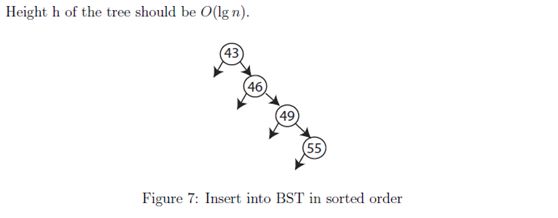
Goal: 系统运行在O(lgn)时间内.
Algorithm
Key Lesson: 我们需要更快的插入方法.
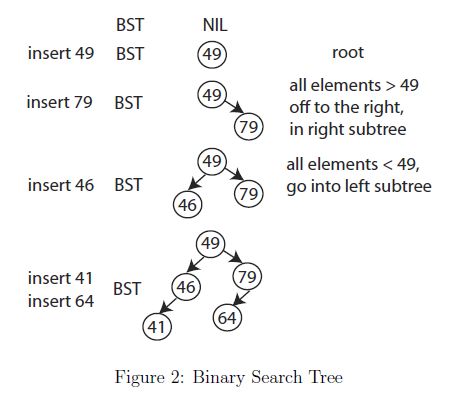
2. 二叉查找树(Binary Search Trees )
二叉查找树的每个节点(node)x都有一个key 为key(x).除去根(Root)外,都有双亲 p(x),可能还有左孩子left(x)或者(and / or)有右孩子right(x).
对于每个节点x,它的左子树上的任意一点都有key(y) ≤key(x); 它的右子树上的任意一点都有key(y) ≧key(x).
python代码:
class BSTnode(object):
"""
Representation of a node in a binary search tree.
Has a left child, right child, and key value, and stores its subtree size.
"""
def __init__(self, parent, t):
"""Create a new leaf with key t."""
self.key = t
self.parent = parent
self.left = None
self.right = None
self.size = 1
def update_stats(self):
"""Updates this node's size based on its children's sizes."""
self.size = (0 if self.left is None else self.left.size) + (0 if self.right is None else self.right.size)
def insert(self, t, NodeType):
"""Insert key t into the subtree rooted at this node (updating subtree size)."""
self.size += 1
if t < self.key:
if self.left is None:
self.left = NodeType(self, t)
return self.left
else:
return self.left.insert(t, NodeType)
else:
if self.right is None:
self.right = NodeType(self, t)
return self.right
else:
return self.right.insert(t, NodeType)
def find(self, t):
"""Return the node for key t if it is in this tree, or None otherwise."""
if t == self.key:
return self
elif t < self.key:
if self.left is None:
return None
else:
return self.left.find(t)
else:
if self.right is None:
return None
else:
return self.right.find(t)
def rank(self, t):
"""Return the number of keys <= t in the subtree rooted at this node."""
left_size = 0 if self.left is None else self.left.size
if t == self.key:
return left_size + 1
elif t < self.key:
if self.left is None:
return 0
else:
return self.left.rank(t)
else:
if self.right is None:
return left_size + 1
else:
return self.right.rank(t) + left_size + 1
def minimum(self):
"""Returns the node with the smallest key in the subtree rooted by this node."""
current = self
while current.left is not None:
current = current.left
return current
def successor(self):
"""Returns the node with the smallest key larger than this node's key, or None if this has the largest key in the tree."""
if self.right is not None:
return self.right.minimum()
current = self
while current.parent is not None and current.parent.right is current:
current = current.parent
return current.parent
def delete(self):
""""Delete this node from the tree."""
if self.left is None or self.right is None:
if self is self.parent.left:
self.parent.left = self.left or self.right
if self.parent.left is not None:
self.parent.left.parent = self.parent
else:
self.parent.right = self.left or self.right
if self.parent.right is not None:
self.parent.right.parent = self.parent
current = self.parent
while current.key is not None:
current.update_stats()
current = current.parent
return self
else:
s = self.successor()
self.key, s.key = s.key, self.key
return s.delete()
def check(self, lokey, hikey):
"""Checks that the subtree rooted at t is a valid BST and all keys are between (lokey, hikey)."""
if lokey is not None and self.key <= lokey:
raise "BST RI violation"
if hikey is not None and self.key >= hikey:
raise "BST RI violation"
if self.left is not None:
if self.left.parent is not self:
raise "BST RI violation"
self.left.check(lokey, self.key)
if self.right is not None:
if self.right.parent is not self:
raise "BST RI violation"
self.right.check(self.key, hikey)
if self.size != 1 + (0 if self.left is None else self.left.size) + (0 if self.right is None else self.right.size):
raise "BST RI violation"
def __repr__(self):
return "<BST Node, key:" + str(self.key) + ">"
class BST(object):
"""
Simple binary search tree implementation, augmented with subtree sizes.
This BST supports insert, find, and delete-min operations.
Each tree contains some (possibly 0) BSTnode objects, representing nodes,
and a pointer to the root.
"""
def __init__(self, NodeType=BSTnode):
self.root = None
self.NodeType = NodeType
self.psroot = self.NodeType(None, None)
def reroot(self):
self.root = self.psroot.left
def insert(self, t):
"""Insert key t into this BST, modifying it in-place."""
if self.root is None:
self.psroot.left = self.NodeType(self.psroot, t)
self.reroot()
return self.root
else:
return self.root.insert(t, self.NodeType)
def find(self, t):
"""Return the node for key t if is in the tree, or None otherwise."""
if self.root is None:
return None
else:
return self.root.find(t)
def rank(self, t):
"""The number of keys <= t in the tree."""
if self.root is None:
return 0
else:
return self.root.rank(t)
def delete(self, t):
"""Delete the node for key t if it is in the tree."""
node = self.find(t)
deleted = node.delete()
self.reroot()
return deleted
def check(self):
if self.root is not None:
self.root.check(None, None)
def __str__(self):
if self.root is None: return '<empty tree>'
def recurse(node):
if node is None: return [], 0, 0
label = str(node.key)
left_lines, left_pos, left_width = recurse(node.left)
right_lines, right_pos, right_width = recurse(node.right)
middle = max(right_pos + left_width - left_pos + 1, len(label), 2)
pos = left_pos + middle // 2
width = left_pos + middle + right_width - right_pos
while len(left_lines) < len(right_lines):
left_lines.append(' ' * left_width)
while len(right_lines) < len(left_lines):
right_lines.append(' ' * right_width)
if (middle - len(label)) % 2 == 1 and node.parent is not None and \
node is node.parent.left and len(label) < middle:
label += '.'
label = label.center(middle, '.')
if label[0] == '.': label = ' ' + label[1:]
if label[-1] == '.': label = label[:-1] + ' '
lines = [' ' * left_pos + label + ' ' * (right_width - right_pos),
' ' * left_pos + '/' + ' ' * (middle-2) +
'\\' + ' ' * (right_width - right_pos)] + \
[left_line + ' ' * (width - left_width - right_width) +
right_line
for left_line, right_line in zip(left_lines, right_lines)]
return lines, pos, width
return '\n'.join(recurse(self.root) [0])
我们解决完所有的问题了吗?