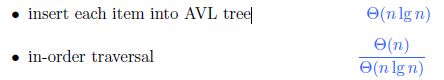MIT Introduction to Algorithms 学习笔记(七)
Lecture 6: Balanced Binary Search Trees
AVL树
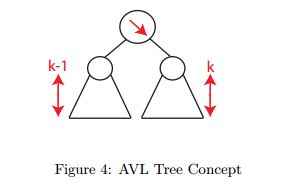
定义: AVL树是自平衡二叉查找树, 每个结点的左右子树的高度之差的绝对值(平衡因子)最多为1.
平衡(Balance):平衡最坏的情况是每个节点高度差1.
AVL 插入:
1. insert as in simple BST
2. work your way up tree, restoring AVL property (and updating heights as you go).
步骤:
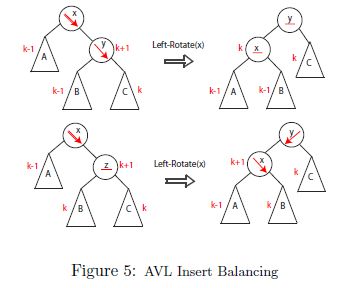
suppose x is lowest node violating AVL .
assume x is right-heavy (left case symmetric)
if x's right child is right-heavy or balanced: follow steps in Fig. 5
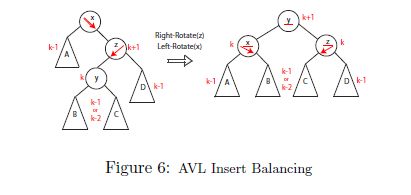
else: follow steps in Fig. 6
then continue up to x's grandparent, greatgrandparent . . .
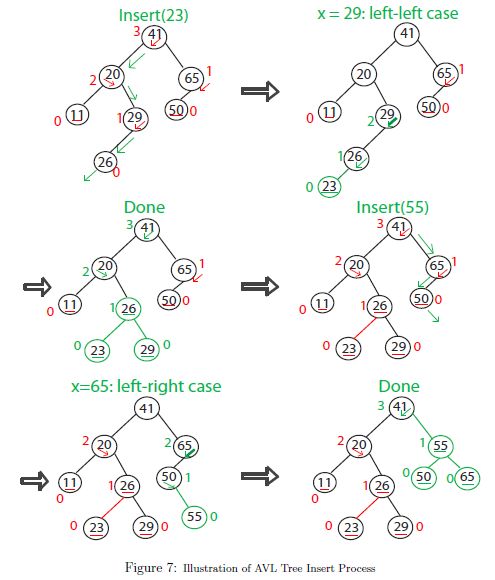
Example:
AVL 排序:
代码
'''
Created on 20151223
@author: Administrator
'''
class BST(object):
'''
classdocs
'''
def __init__(self):
'''
Constructor
'''
self.root = None
def insert(self,t):
newNode = BSTnode(t)
if(self.root is None):
self.root = newNode
else:
node = self.root
while(True):
if(t < node.key):
if(node.left is None):
node.left = newNode
newNode.parent = node
break
node = node.left
else:
if(node.right is None):
node.right = newNode
newNode.parent = node
break
node = node.right
return newNode
def find(self,t):
node = self.root
while (node is not None):
if(t == node.key):
return node
elif(t < node.key):
node = node.left
else:
node = node.right
return None
def find_min(self):
node = self.root
while(node is not None):
if(node.left is None):
return node
else:
node = node.left
return None
def delete_min(self):
"""Delete the minimum key (and return the old node containing it)."""
if self.root is None:
return None, None
else:
# Walk to leftmost node.
node = self.root
while node.left is not None:
node = node.left
# Remove that node and promote its right subtree.
if node.parent is not None:
node.parent.left = node.right
else: # The root was smallest.
self.root = node.right
if node.right is not None:
node.right.parent = node.parent
parent = node.parent
node.disconnect()
return node, parent
def __str__(self):
if self.root is None: return '<empty tree>'
def recurse(node):
if node is None: return [], 0, 0
label = str(node.key)
left_lines, left_pos, left_width = recurse(node.left)
right_lines, right_pos, right_width = recurse(node.right)
middle = max(right_pos + left_width - left_pos + 1, len(label), 2)
pos = left_pos + middle // 2
width = left_pos + middle + right_width - right_pos
while len(left_lines) < len(right_lines):
left_lines.append(' ' * left_width)
while len(right_lines) < len(left_lines):
right_lines.append(' ' * right_width)
if (middle - len(label)) % 2 == 1 and node.parent is not None and \
node is node.parent.left and len(label) < middle:
label += '.'
label = label.center(middle, '.')
if label[0] == '.': label = ' ' + label[1:]
if label[-1] == '.': label = label[:-1] + ' '
lines = [' ' * left_pos + label + ' ' * (right_width - right_pos),
' ' * left_pos + '/' + ' ' * (middle-2) +
'\\' + ' ' * (right_width - right_pos)] + \
[left_line + ' ' * (width - left_width - right_width) +
right_line
for left_line, right_line in zip(left_lines, right_lines)]
return lines, pos, width
return '\n'.join(recurse(self.root) [0])
class BSTnode(object):
"""
Representation of a node in a binary search tree.
Has a left child, right child, and key value.
"""
def __init__(self,t):
self.key = t
self.disconnect()
def disconnect(self):
self.left = None
self.right = None
self.parent = None
def height(node):
if node is None:
return -1
else:
return node.height
def update_height(node):
node.height = max(height(node.left), height(node.right)) + 1
class AVL(BST):
"""
AVL binary search tree implementation.
Supports insert, find, and delete-min operations in O(lg n) time.
"""
def left_rotate(self, x):
print("left_rotate")
y = x.right
y.parent = x.parent
if y.parent is None:
self.root = y
else:
if y.parent.left is x:
y.parent.left = y
elif y.parent.right is x:
y.parent.right = y
x.right = y.left
if x.right is not None:
x.right.parent = x
y.left = x
x.parent = y
update_height(x)
update_height(y)
def right_rotate(self, x):
print("right_rotate")
y = x.left
y.parent = x.parent
if y.parent is None:
self.root = y
else:
if y.parent.left is x:
y.parent.left = y
elif y.parent.right is x:
y.parent.right = y
x.left = y.right
if x.left is not None:
x.left.parent = x
y.right = x
x.parent = y
update_height(x)
update_height(y)
def insert(self, t):
"""Insert key t into this tree, modifying it in-place."""
node = BST.insert(self, t)
self.rebalance(node)
def rebalance(self, node):
print("rebalance")
while node is not None:
#print("node = " +str(node.key) +" height = ",node.height)
update_height(node)
if height(node.left) >= 2 + height(node.right):
if height(node.left.left) >= height(node.left.right):
self.right_rotate(node)
else:
self.left_rotate(node.left)
self.right_rotate(node)
elif height(node.right) >= 2 + height(node.left):
if height(node.right.right) >= height(node.right.left):
self.left_rotate(node)
else:
self.right_rotate(node.right)
self.left_rotate(node)
node = node.parent
def delete_min(self):
node, parent = BST.delete_min(self)
self.rebalance(parent)
#raise NotImplemented('AVL.delete_min')
test1 = range(0, 100, 10)
test2 = [31, 41, 59, 26, 53, 58, 97, 93, 73]
test3 = "algorithms"
#import random
def test(args=None, BSTtype=AVL):
items = test2
tree = BSTtype()
print (tree)
for item in items:
tree.insert(item)
print("------------------------------------------")
print (tree)
tree.delete_min()
print("------------------------------------------")
print(tree)
if __name__ == '__main__': test()