遗传算法解决旅行商问题(TSP)

这次的文章是以一份报告的形式贴上来，代码只是简单实现，难免有漏洞，比如循环输入的控制条件，说是要求输入1，只要输入非0就行。希望会帮到以后的同学(*＾-＾*)

一、问题描述

   旅行商问题(Traveling-Salesman Problem,TSP)。设有n个互相可直达的城市，某推销商准备从其中的A城出发，周游各城市一遍，最后又回到A城。要求为该旅行商规划一条最短的旅行路线。

二、目的

   为了解决旅行商问题，用了遗传算法，模拟染色体的遗传过程，进行求解。

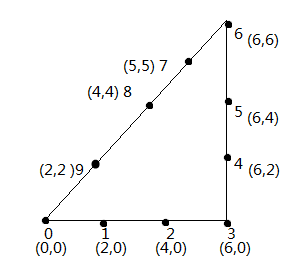
   为了直观的更有比较性的观察到程序的运行效果，我这里程序里给定了10个城市的坐标，并计算出其任意两个的欧氏距离，10个点的位置排布见图1。程序的理想最优距离为20.485281，即绕三角形一圈，而且路程起点不固定，因为只要满足点围着三角形一圈即为最短距离，最优解。所以问题转换为，求图中10 个点的不重复点的闭环序列的距离最小值。

                   

                                       图 1

三、原理

1、内部变量介绍 

程序总体围绕了遗传算法的三个主要步骤：选择--复制，交叉，变异。给定了10个种群，即10条染色体，每条染色体都是除首位外不重复的点组成，首尾相同保证路线是闭合的，所以一条染色体包含11个点。

种群由一个结构体group表示，内含城市的序列int city[11]、种群的适应度double fit、该种群适应度占总群体适应度的比例double p，和为了应用赌轮选择机制的积累概率 double jlleigailv。

程序还包括一个始终记录所有种群中的最优解的城市序列数组groupbest[11]，记录最优解的适应度，即最大适应度的变量 double groupbestfit。

种群的最大繁衍代数设置为1000，用户能够输入繁衍代数，但必须在1000以内。10个点的不同排列序列有10！种，即3628800中排列可能，其中各代之间可能产生重复，不同种群间也会出现重复，学生觉得1000左右应该能验证程序的性能了，就定为1000。

2、运行思想介绍

(a)采用整数编码的方式，标记0到9号城市。

(b)选择--复制：

利用赌轮选择机制，分10次从10个种群中挑选出10个染色体进行复制。

每次随机生成一个0到1之内的小数，因为适应度越高的染色体的积累概率区间越大，所以适应度越高的染色体被选择的次数会越多，满足了优胜劣汰的原则。

选择--复制完后，要重新计算每个种群的适应度等信息，与已经保存的最优染色体进行比较，如果比已经存在的适应度还要高就进行最优染色体的更新。如果最优染色体没有更新，则说明新成的最大适应度种群不如以前的好，则在新生成的种群中找到适应度最低的，用最优染色体提换掉。

(c)交叉：

    每一代的繁衍都让10个种群中相邻的两个种群进行染色体交叉，交叉率为1，即0号种群和1号种群交叉，2号种群和3号种群交叉，以此类推。交叉段是由2个随机数决定，采用部分映射交叉，直接交换由随机数产生的染色体片段。

交叉完后因为要满足点的不重复，所以要进行消除重复的操作。原理是用一个数组保留交叉过来的染色体片段，删除染色体上已经交换的片段，在剩下的点中消除与新交换片段中重复的点，然后将原染色体剩下的点都向前移集中在头部，再将保存在数组中的新交换过来的染色体插入到头部之后，在以上过程中用一个数组记录已经存在的点。接下来将没有用的点顺序插到染色体尾部，到此已经生成了新的染色体。

交叉完后要重新计算每个种群的适应度等信息，与已经保存的最优染色体进行比较，如果比已经存在的适应度还要高就进行最优染色体的更新。如果最优染色体没有更新，则说明新成的最大适应度种群不如以前的好，则在新生成的种群中找到适应度最低的，用最优染色体提换掉。

(d)变异：

因为变异在自然界并不是每次都会发生，所有每次要尽行变异前都生成一个0到9内的随机整数，如果大于3就进行变异，否则不变异，总体变异率为0.6。因为这个染色体和自然中的每一段都对应一个功能的染色体不一样，染色体越是按数的相邻大小排列，距离会越短，所以变异就起了很大作用，起到调整点的顺序的作用，所以变异率要大一点。

如果要变异，则变异3次。每次生成2个随机数，决定要在哪个种群变异哪一个位置。比如挑选了第二条染色体，变异第3个位置，则将染色体的3号位和6号位互换，即互换位置和为9。

(e)输出：

输出用户程序得到的最优解的城市序列、路程距离、适应度和在第几代得到的最优解。

程序可以循环多次运行，只要用户按照提示输入。

四、结果

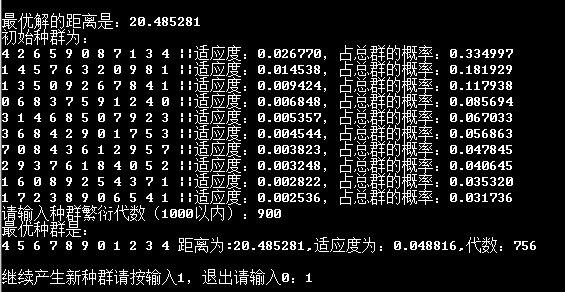
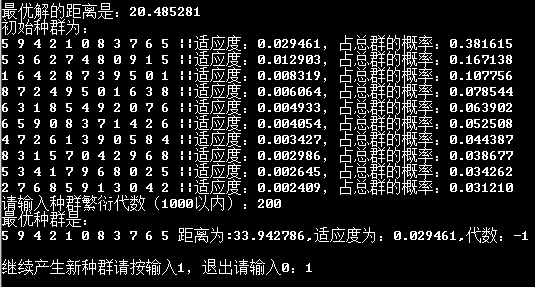
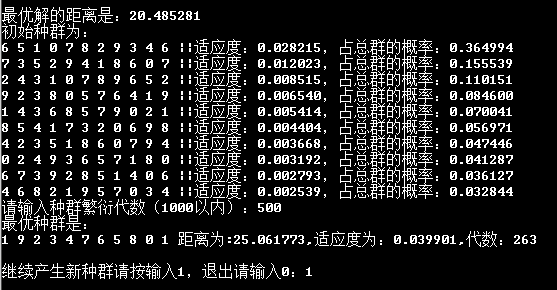
    程序的总体结果又很大随机性，但特别坏的结果毕竟只占少数，多数都是一般结果，多随机运行几次，还有控制繁衍的代数就能够得到比较好的结果。令人振奋的是，经过多次的尝试，又一次输出了理想最优解，正好是围三角形绕一圈，路程距离是20.485281，在第756代生成。一下是程序运行的比较好的结果、比较差的结果的举例，和最优结果的贴图，图2为最优结果。

图2

图3

图4

五、讨论

这次程序--遗传算法解决旅行商问题，的总体思想结合了课本和网上有关内容，但令人振奋的是，上图1给的实例，还有具体的实现代码和里面的具体思想都是出自学生仔细思考的结果，没有抄袭，程序的每一步正确运行都凝聚了学生认真对待的心血。

写这个程序总体上分成了2个步骤，思想理解与构造，具体代码实现。

大约用了1个白天天左右的时间去了解：遗传算法怎么去解决这个问题，怎样进行选择复制，交叉的方法有哪些，变异的方法又有哪些。决定了每一步用的思想后便进行具体敲代码。

敲代码又分成了两段。第一段时间，在开始编码的那天晚上我完成了程序的基本内容，跑一下也没有问题，只是效果有很大随机性，结果不是很好，第二天想了很久，又看了很多资料发现，原因在于交叉选择的方法不好。一开始那种方法是，交换后的染色体直接放到相邻染色体的相应位置，在其他地方进行消除重复的操作，染色体上会出现很多空洞，然后用没有用过的点顺序插在空洞里，构成新的染色体。后来我想了很久，吃饭时走在路上一想，不对啊，这样有可能完全破坏了原来的优秀队列，因为这个优秀染色体就是由排列顺序决定的。回来后就修改了交叉的算法，形成了现在的算法，这样能够最大程度的保留原来的顺序，又能很大可能获得新的优秀队列。

程序有400多行，交叉算法用的变量多而且又复杂，其中用来找bug的时间比较多，敲代码的时候有很多细节问题脑子一开始想好了的，没有敲上去。而且一边敲，一边也在对原由思想进行改进。

总之，遗传算法的可移植性很大，可以用来逼近很多问题的最优解，实在是很厉害。做了这么多，我真的感觉收获良多，一些细节处的bug好烦人，希望以后自己能够更加细心。

六、代码

里面的思想在前面已经讲了，但里面的变量我设的时候标注的不是很清楚，思想懂了，代码完全可以自己写出来的(*＾-＾*)

  1 #include<stdio.h>
  2 #include<string.h>
  3 #include<time.h>
  4 #include<math.h>
  5 
  6 double distance[10][11];//城市之间的距离 
  7 int dai,die;
  8 int cities[2][10];//记录城市坐标
  9 int citynum=10;
 10 int groupbest[11];//最优解染色体 
 11 double groupbestp;//最优解的p 
 12 double groupbestfit;//最优解的fit 
 13 int changebest;//要不要用最优解替代新种群 
 14 
 15 struct group
 16 {
 17   int city[11];//一维记录城市序号，二三维记录坐标
 18   double p;//占总群的概率 
 19   double fit;//适应度 
 20   double jileigailv;
 21 }group[10];
 22 
 23 /*用来计算种群的p、fit*/
 24 void jisuan() 
 25 {
 26   int i,j,k;
 27   double ss,s;
 28   s=0.0;
 29   ss=0.0;
 30   for(k=0;k<10;k++)
 31   {
 32     for(i=0;i<citynum;i++)
 33         {
 34           s+=distance[group[k].city[i]][group[k].city[i+1]];
 35         }
 36     group[k].fit=1.0/s;
 37     ss+=group[k].fit;
 38   }
 39   s=0.0;
 40   for(i=0;i<10;i++)
 41   {
 42   group[i].p=group[i].fit/ss;
 43   s+=group[i].p;
 44   group[i].jileigailv=s;
 45   } 
 46 }
 47 /*保存最优解*/ 
 48 void savebest()
 49 {
 50   int i,j,flag=0;
 51   double fit=groupbestfit;
 52   j=0;
 53   for(i=0;i<10;i++)
 54   {
 55      if(group[i].fit>fit)
 56      {
 57        j=i;
 58        fit=group[i].fit;
 59        flag=1;//标记已经有更好的 
 60      }
 61   }
 62      if(flag)
 63      {
 64          dai=die;
 65        for(i=0;i<citynum+1;i++)//保存最优解
 66        {
 67           groupbest[i]=group[j].city[i];
 68        }
 69        groupbestp=group[j].p;
 70        changebest=0; 
 71        groupbestfit=group[j].fit;
 72      }
 73      else
 74       changebest=1;//说明新生成的解还不如原来的好，要进行替换
 75 }
 76 /*用最优解替代新种群中的最差的染色体*/
 77 void changebestgroup()
 78 {
 79   int j,i;
 80   double fit=group[0].fit;
 81   j=0;
 82   if(changebest)
 83   {
 84     for(i=1;i<10;i++)
 85     {
 86       if(group[i].fit<fit)
 87       {
 88         fit=group[i].fit;
 89         j=i;
 90       }
 91     }
 92     for(i=0;i<citynum+1;i++)
 93     {
 94       group[j].city[i]=groupbest[i];
 95     }
 96     jisuan();
 97   }
 98 }
 99 /*初始种群和城市坐标，计算距离*/ 
100 void chushigroup()
101 {
102   int i,j,t,flag,k;
103   double ss;
104   cities[0][0]=0;//初始化坐标
105   cities[1][0]=0;
106   cities[0][1]=2;
107   cities[1][1]=0;
108   cities[0][2]=4;
109   cities[1][2]=0;
110   cities[0][3]=6;
111   cities[1][3]=0;
112   cities[0][4]=6;
113   cities[1][4]=2;
114   cities[0][5]=6;
115   cities[1][5]=4;
116   cities[0][6]=6;
117   cities[1][6]=6;
118   cities[0][7]=5;
119   cities[1][7]=5;
120   cities[0][8]=4;
121   cities[1][8]=4;
122   cities[0][9]=2;
123   cities[1][9]=2;
124 memset(groupbest,-1,sizeof(groupbest));
125 groupbestp=0.0;
126 groupbestfit=0.0;
127 changebest=0;
128   for(i=0;i<citynum;i++)
129     for(j=0;j<=i;j++)
130     {
131       if(j==i)
132           distance[i][j]=0.0;
133       else
134       {
135           distance[i][j]=sqrt(pow(cities[0][i]-cities[0][j],2.0)+pow(cities[1][i]-cities[1][j],2.0));//欧氏距离
136           distance[j][i]=distance[i][j];
137       }
138     }
139   printf("最优解的距离是：%f\n",distance[0][1]+distance[1][2]+distance[2][3]+distance[3][4]+distance[4][5]+distance[5][6]+distance[6][7]+distance[7][8]+distance[8][9]+distance[9][0]);
140   srand((unsigned)time(NULL));
141   ss=0;
142   for(k=0;k<10;k++)
143   {//一个数量为10的种群，和10 个城市环 
144     for(i=0;i<citynum;i++)
145     {
146         flag=1;
147         while(flag)
148         {
149           t=rand()%citynum;
150            for(j=0;j<i;j++)
151           {
152             if(group[k].city[j]==t)
153             {
154               break;
155             }
156           }
157             if(j==i)
158             {
159               group[k].city[i]=t;
160               flag=0;
161             }
162          }
163      }
164    group[k].city[10]= group[k].city[0];
165   }
166   //以上产生了10 个种群，分别有不重复的染色体
167 
168 jisuan();
169 savebest();
170 printf("初始种群为：\n");
171 for(i=0;i<10;i++)
172 {
173   for(j=0;j<citynum+1;j++)
174       printf("%d ",group[i].city[j]);
175   printf("||适应度：%f，占总群的概率：%f\n",group[i].fit,group[i].p);
176 }
177 }
178 /*选择--复制*/ 
179 void xuanze()
180 {
181   int i,j,temp[10][11],k;
182   double t;
183   srand((unsigned)time(NULL));
184   for(i=0;i<10;i++) //选10条染色体出来复制,赌轮
185   {
186     t=rand()%10000*1.0/10000;
187     for(j=0;j<10;j++)
188     {
189         
190       if(t<=group[j].jileigailv)
191       {
192           for(k=0;k<citynum+1;k++)
193           {
194             temp[i][k]=group[j].city[k];
195           }
196           break; 
197       } 
198     }
199   }
200   //拷贝新种群
201   for(i=0;i<10;i++)
202     for(j=0;j<citynum+1;j++)
203     {
204       group[i].city[j]=temp[i][j];
205     }
206     jisuan();
207     savebest();
208     changebestgroup();
209 }
210 /*交叉*/ 
211 void jiaocha()
212 {
213   int point1,point2,temp,i,j,k,temp3[2][10],temp2[2][10],num,write;
214   srand((unsigned)time(NULL));
215   point1=rand()%10;
216   point2=rand()%10;
217   if(point1>point2)
218   {
219     temp=point1;
220     point1=point2;
221     point2=temp;
222   }
223   //交换,每2条交换
224  if(point1!=point2)
225  {
226   for(j=1;j<10;j=j+2)
227   {
228        memset(temp3,-1,sizeof(temp3));
229        memset(temp2,-1,sizeof(temp2));
230        k=0;
231     for(i=point1;i<=point2;i++)
232     {
233      temp2[0][k]=group[j].city[i];
234      temp2[1][k]=group[j-1].city[i];
235      temp3[0][temp2[0][k]]=1;//标记数字已经存在了
236      temp3[1][temp2[1][k]]=1;
237      k++;
238      group[j].city[i]=-1;
239      group[j-1].city[i]=-1;
240     }
241     num=point2-point1+1;//交换的位数 
242      //消重
243     for(k=0;k<point1;k++)
244       {
245         if(temp3[0][group[j-1].city[k]]==1)
246         {
247            group[j-1].city[k]=-1;
248         }
249         else
250            temp3[0][group[j-1].city[k]]=1;
251       } 
252       for(k=point2+1;k<citynum;k++)
253       {
254         if(temp3[0][group[j-1].city[k]]==1)
255         {
256            group[j-1].city[k]=-1;
257         }
258         else
259            temp3[0][group[j-1].city[k]]=1;
260       }
261       for(k=0;k<point1;k++)
262       {
263         if(temp3[1][group[j].city[k]]==1)
264         {
265            group[j].city[k]=-1;
266         }
267         else
268            temp3[1][group[j].city[k]]=1;
269       } 
270       for(k=point2+1;k<citynum;k++)
271       {
272         if(temp3[1][group[j].city[k]]==1)
273         {
274            group[j].city[k]=-1;
275         }
276         else
277            temp3[1][group[j].city[k]]=1;
278       }
279       write=0; 
280       for(i=0;i<10;i++)
281       {
282       while(write<10&&group[j-1].city[write]==-1)
283       {
284         write++;
285       }
286       if(write<10)
287       {
288         temp=group[j-1].city[i];
289         group[j-1].city[i]=group[j-1].city[write];
290         group[j-1].city[write]=temp;
291         write++;
292       }
293       else
294       {
295           write=0;
296       for(k=i;k<10;k++)
297       {
298           group[j-1].city[k]=temp2[0][write++];
299           if(write==num)
300           break;
301        }
302       break;
303       }
304     } 
305      write=0; 
306      for(i=0;i<10;i++)
307      {
308       while(write<10&&group[j].city[write]==-1)
309       {
310         write++;
311       }
312       if(write<10)
313       {
314         temp=group[j].city[i];
315         group[j].city[i]=group[j].city[write];
316         group[j].city[write]=temp;
317         write++;
318       }
319       else
320       {
321           write=0;
322         for(k=i;k<10;k++)
323         {
324           group[j].city[k]=temp2[1][write++];
325           if(write==num)
326               break;
327          }
328         break;
329       }
330     } 
331     k=0;
332     for(i=0;i<citynum;i++)
333     {
334        if(group[j-1].city[i]==-1)
335        {
336          while(temp3[0][k]==1&&k<10)
337          {
338            k++;
339          }
340          group[j-1].city[i]=k++;
341        }
342     }
343     k=0;
344     for(i=0;i<citynum;i++)
345     {
346        if(group[j].city[i]==-1)
347        {
348          while(temp3[1][k]==1&&k<10)
349          {
350            k++;
351          }
352          group[j].city[i]=k++;
353        }
354     }
355    group[j].city[10]=group[j].city[0];
356    group[j-1].city[10]=group[j-1].city[0];
357   }//end of j
358  jisuan();
359  savebest();
360  changebestgroup();
361  } //end of if(!)
362 }
363 /*变异*/ 
364 void bianyi()
365 {
366    int t1,t2,temp,t,s=3;
367    srand((unsigned)time(NULL));
368    t=rand()%10;
369    if(t>3)//变异率为3/5 
370    {
371        //挑1个不同的变异，只交换一位
372     t1=rand()%10;//种群 
373     t2=rand()%10;//变换位
374     temp=group[t1].city[t2];
375     group[t1].city[t2]=group[t1].city[9-t2];
376     group[t1].city[9-t2]=temp;
377     group[t1].city[10]=group[t1].city[0];   
378    }
379    jisuan();
380    savebest();
381    changebestgroup();
382 }
383 /*主函数*/
384 int  main()//最优解20.485281
385 {
386   int j,flag,tuichu=1;
387   double distancenum;
388   while(tuichu)
389   {
390     distancenum=0.0;
391     flag=1;
392     chushigroup();
393     while(flag)
394     {
395     printf("请输入种群繁衍代数（1000以内）：");
396     scanf("%d",&die);
397     if(die<=1000)
398     {
399     flag=0;
400     }
401   }
402   while(die--)
403   {
404      xuanze();
405      jiaocha();
406      bianyi();
407   }
408  printf("最优种群是：\n");
409       for(j=0;j<citynum+1;j++)
410       {
411         printf("%d ",groupbest[j]);
412         if(j<citynum)
413         {
414         distancenum+=distance[groupbest[j]][groupbest[j+1]];
415         }
416       }
417       printf("距离为:%f,适应度为：%f,代数：%d\n\n",distancenum,groupbestfit,dai);
418       printf("继续产生新种群请按输入1，退出请输入0：");
419       scanf("%d",&tuichu); 
420       printf("\n");
421     }
422       return 0;
423 }