跳表SkipList

原文: http://www.cnblogs.com/xuqiang/archive/2011/05/22/2053516.html

leveldb中memtable的思想本质上是一个skiplist.

 

<1>. 聊一聊作者的其人其事 

跳表是由William Pugh发明。他在 Communications of the ACM June 1990, 33(6) 668-676 发表了Skip lists: a probabilistic alternative to balanced trees，在该论文中详细解释了跳表的数据结构和插入删除操作。

William Pugh同时还是FindBug（没有使用过，这是一款java的静态代码分析工具，直接对java 的字节码进行分析，能够找出java字节码中潜在很多错误。）作者之一。现在是University of Maryland, College Park（马里兰大学伯克分校，位于马里兰州，全美大学排名在五六十名左右的样子）大学的一名教授。他和他的学生所作的研究深入的影响了java语言中内存池实现。

又是一个计算机的天才！

<2>. 言归正传，跳表简介 

这是跳表的作者，上面介绍的William Pugh给出的解释：

Skip lists are a data structure that can be used in place of balanced trees. Skip lists use probabilistic balancing rather than strictly enforced balancing and as a result the algorithms for insertion and deletion in skip lists are much simpler and significantly faster than equivalent algorithms for balanced trees.

跳表是平衡树的一种替代的数据结构，但是和红黑树不相同的是，跳表对于树的平衡的实现是基于一种随机化的算法的，这样也就是说跳表的插入和删除的工作是比较简单的。

下面来研究一下跳表的核心思想：

先从链表开始，如果是一个简单的链表，那么我们知道在链表中查找一个元素I的话，需要将整个链表遍历一次。

 

 如果是说链表是排序的，并且节点中还存储了指向前面第二个节点的指针的话，那么在查找一个节点时，仅仅需要遍历N/2个节点即可。

 

这基本上就是跳表的核心思想，其实也是一种通过“空间来换取时间”的一个算法，通过在每个节点中增加了向前的指针，从而提升查找的效率。

<3>.跳表的数据存储模型 

 我们定义：

如果一个基点存在k个向前的指针的话，那么陈该节点是k层的节点。

一个跳表的层MaxLevel义为跳表中所有节点中最大的层数。

下面给出一个完整的跳表的图示：

 

 那么我们该如何将该数据结构使用二进制存储呢？通过上面的跳表的很容易设计这样的数据结构：

定义每个节点类型：

// 这里仅仅是一个指针

typedef struct nodeStructure *node;

typedef struct nodeStructure

{

    keyType key; // key值

    valueType value; // value值

    // 向前指针数组，根据该节点层数的

    // 不同指向不同大小的数组

    node forward[1];

};

 

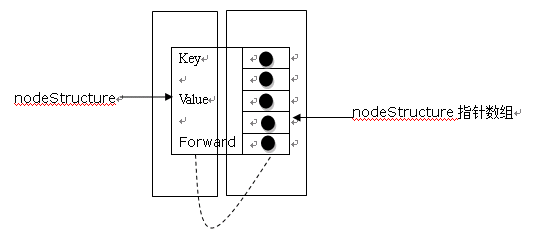
上面的每个结构体对应着图中的每个节点，如果一个节点是一层的节点的话（如7，12等节点），那么对应的forward将指向一个只含一个元素的数组，以此类推。

 定义跳表数据类型：

// 定义跳表数据类型

typedef struct listStructure{

   int level;    /* Maximum level of the list 

(1 more than the number of levels in the list) */

   struct nodeStructure * header; /* pointer to header */

   } * list; 

跳表数据类型中包含了维护跳表的必要信息，level表明跳表的层数，header如下所示：

 

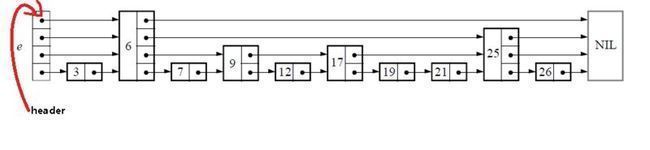
定义辅助变量：

定义上图中的NIL变量：node NIL;

#define MaxNumberOfLevels 16

#define MaxLevel (MaxNumberOfLevels-1) 

定义辅助方法：

 

// newNodeOfLevel生成一个nodeStructure结构体，同时生成l个node *数组指针

#define newNodeOfLevel(l) (node)malloc(sizeof(struct nodeStructure)+(l)*sizeof(node *))

好的基本的数据结构定义已经完成，接下来来分析对于跳表的一个操作。 

<4>. 跳表的代码实现分析 

4.1 初始化

初始化的过程很简单，仅仅是生成下图中红线区域内的部分，也就是跳表的基础结构：

 

list newList()

{

  list l;

  int i;

  // 申请list类型大小的内存

  l = (list)malloc(sizeof(struct listStructure));

  // 设置跳表的层level，初始的层为0层（数组从0开始）

  l->level = 0;

  

  // 生成header部分

  l->header = newNodeOfLevel(MaxNumberOfLevels);

  // 将header的forward数组清空

  for(i=0;i<MaxNumberOfLevels;i++) l->header->forward[i] = NIL;

  return(l);

};  

4.2 插入操作

由于跳表数据结构整体上是有序的，所以在插入时，需要首先查找到合适的位置，然后就是修改指针（和链表中操作类似），然后更新跳表的level变量。

 

boolean insert(l,key,value) 

register list l;

register keyType key;

register valueType value;

{

  register int k;

  // 使用了update数组

  node update[MaxNumberOfLevels];

  register node p,q;

 

  p = l->header;

  k = l->level;

  /*******************1步*********************/

  do {

// 查找插入位置

while (q = p->forward[k], q->key < key)

p = q;

 

// 设置update数组

update[k] = p;

} while(--k>=0); // 对于每一层进行遍历

 

// 这里已经查找到了合适的位置，并且update数组已经

// 填充好了元素

   if (q->key == key)

   {

     q->value = value;

  return(false);

  };

 

  // 随机生成一个层数

   k = randomLevel();  

  if (k>l->level) 

  {

   // 如果新生成的层数比跳表的层数大的话

    // 增加整个跳表的层数

k = ++l->level;

// 在update数组中将新添加的层指向l->header

update[k] = l->header;

  };

 

  /*******************2步*********************/

  // 生成层数个节点数目

  q = newNodeOfLevel(k);

  q->key = key;

  q->value = value;

      

  // 更新两个指针域

  do 

  {

p = update[k];

q->forward[k] = p->forward[k];

p->forward[k] = q;

} while(--k>=0);

 

// 如果程序运行到这里，程序已经插入了该节点

 

  return(true);

} 

4.3 删除某个节点

和插入是相同的，首先查找需要删除的节点，如果找到了该节点的话，那么只需要更新指针域，如果跳表的level需要更新的话，进行更新。

 

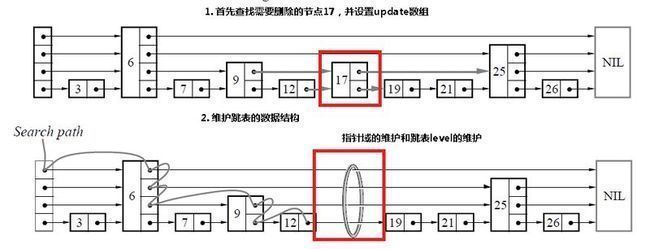
boolean delete(l,key) 

register list l;

register keyType key;

{

  register int k,m;

  // 生成一个辅助数组update

  node update[MaxNumberOfLevels];

  register node p,q;

 

  p = l->header;

  k = m = l->level;

  // 这里和查找部分类似，最终update中包含的是：

  // 指向该节点对应层的前驱节点

  do 

  {

while (q = p->forward[k], q->key < key) 

p = q;

update[k] = p;

} while(--k>=0);

 

// 如果找到了该节点，才进行删除的动作

  if (q->key == key) 

  {

   // 指针运算

for(k=0; k<=m && (p=update[k])->forward[k] == q; k++) 

// 这里可能修改l->header->forward数组的值的 

  p->forward[k] = q->forward[k];

// 释放实际内存

free(q);

 

// 如果删除的是最大层的节点，那么需要重新维护跳表的

// 层数level

    while( l->header->forward[m] == NIL && m > 0 )

     m--;

l->level = m;

return(true);

}

  else

   // 没有找到该节点，不进行删除动作 

   return(false);

} 

4.4 查找

查找操作其实已经在插入和删除过程中包含，比较简单，可以参考源代码。 

<5>. 论文，代码下载及参考资料 

SkipList论文

/Files/xuqiang/skipLists.rar 

 

//--------------------------------------------------------------------------------

增加跳表c#实现代码 2011-5-29下午 

上面给出的数据结构的模型是直接按照跳表的模型得到的，另外还有一种数据结构的模型：

跳表节点类型，每个跳表类型中仅仅存储了左侧的节点和下面的节点：

 

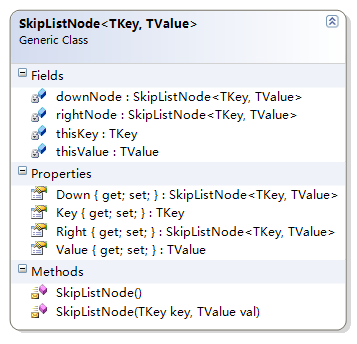
我们现在来看对于这种模型的操作代码：

1. 初始化完成了如下的操作：

 

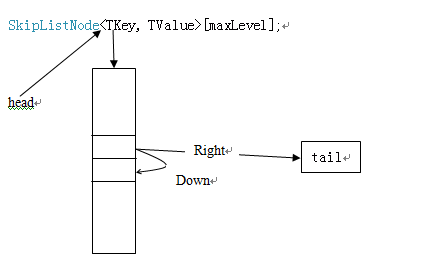
2. 插入操作：和上面介绍的插入操作是类似的，首先查找到插入的位置，生成update数组，然后随机生成一个level，然后修改指针。

3. 删除操作：和上面介绍的删除操作是类似的，查找到需要删除的节点，如果查找不到，抛出异常，如果查找到的需要删除的节点的话，修改指针，释放删除节点的内存。

代码下载：

/Files/xuqiang/skiplist_csharp.rar