Dijkstra 单源最短路径算法

Dijkstra 算法是一种用于计算带权有向图中单源最短路径（SSSP：Single-Source Shortest Path）的算法，由计算机科学家 Edsger Dijkstra 于 1956 年构思并于 1959 年发表。其解决的问题是：给定图 G 和源顶点 v，找到从 v 至图中所有顶点的最短路径。

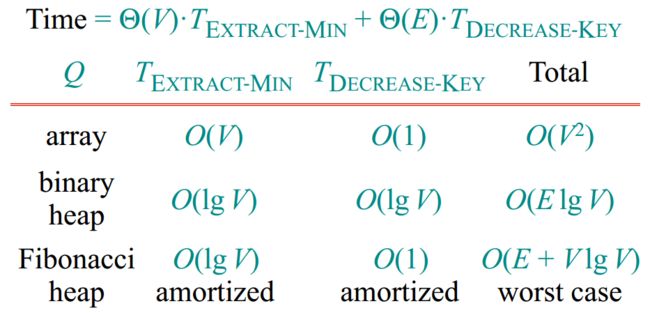
Dijkstra 算法采用贪心算法（Greedy Algorithm）范式进行设计。在最短路径问题中，对于带权有向图 G = (V, E)，Dijkstra 算法的初始实现版本未使用最小优先队列实现，其时间复杂度为 O(V²)，基于 Fibonacci heap 的最小优先队列实现版本，其时间复杂度为 O(E + VlogV)。

Bellman-Ford 算法和 Dijkstra 算法同为解决单源最短路径的算法。对于带权有向图 G = (V, E)，Dijkstra 算法要求图 G 中边的权值均为非负，而 Bellman-Ford 算法能适应一般的情况（即存在负权边的情况）。一个实现的很好的 Dijkstra 算法比 Bellman-Ford 算法的运行时间 O(V*E) 要低。

Dijkstra 算法描述：

1. 创建源顶点 v 到图中所有顶点的距离的集合 distSet，为图中的所有顶点指定一个距离值，初始均为 Infinite，源顶点距离为 0；
2. 创建 SPT（Shortest Path Tree）集合 sptSet，用于存放包含在 SPT 中的顶点；
3. 如果 sptSet 中并没有包含所有的顶点，则：
   • 选中不包含在 sptSet 中的顶点 u，u 为当前 sptSet 中未确认的最短距离顶点；
   • 将 u 包含进 sptSet；
   • 更新 u 的所有邻接顶点的距离值；

伪码实现如下：

 1 function Dijkstra(Graph, source):
 2 
 3     dist[source] ← 0          // Distance from source to source
 4     prev[source] ← undefined  // Previous node in optimal path initialization
 5 
 6     for each vertex v in Graph:  // Initialization
 7         if v ≠ source            // Where v has not yet been removed from Q (unvisited nodes)
 8             dist[v] ← infinity   // Unknown distance function from source to v
 9             prev[v] ← undefined  // Previous node in optimal path from source
10         end if 
11         add v to Q               // All nodes initially in Q (unvisited nodes)
12     end for
13     
14     while Q is not empty:
15         u ← vertex in Q with min dist[u]  // Source node in first case
16         remove u from Q 
17         
18         for each neighbor v of u:         // where v has not yet been removed from Q.
19             alt ← dist[u] + length(u, v)
20             if alt < dist[v]:             // A shorter path to v has been found
21                 dist[v] ← alt 
22                 prev[v] ← u 
23             end if
24         end for
25     end while
26 
27     return dist[], prev[]
28 
29 end function

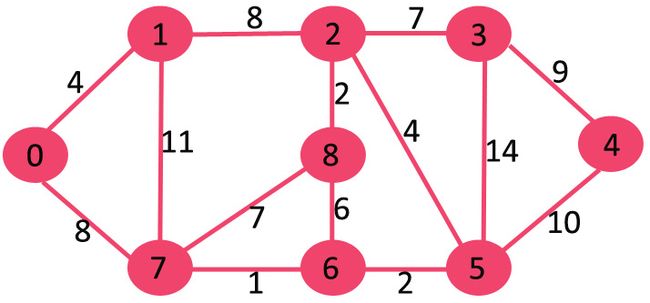
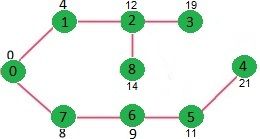
例如，下面是一个包含 9 个顶点的图，每条边分别标识了距离。

源顶点 source = 0，初始时，

• sptSet = {false, false, false, false, false, false, false, false, false};
• distSet = {0, INF, INF, INF, INF, INF, INF, INF, INF};

将 0 包含至 sptSet 中；

• sptSet = {true, false, false, false, false, false, false, false, false};

更新 0 至其邻接节点的距离；

• distSet = {0, 4, INF, INF, INF, INF, INF, 8, INF};

选择不在 sptSet 中的 Min Distance 的顶点，为顶点 1，则将 1 包含至 sptSet；

• sptSet = {true, true, false, false, false, false, false, false, false};

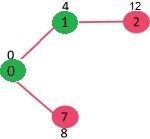
更新 1 至其邻接节点的距离；

• distSet = {0, 4, 12, INF, INF, INF, INF, 8, INF};

选择不在 sptSet 中的 Min Distance 的顶点，为顶点 7，则将 7 包含至 sptSet；

• sptSet = {true, true, false, false, false, false, false, true, false};

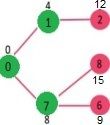
更新 7 至其邻接节点的距离；

• distSet = {0, 4, 12, INF, INF, INF, 9, 8, 15};

选择不在 sptSet 中的 Min Distance 的顶点，为顶点 6，则将 6 包含至 sptSet；

• sptSet = {true, true, false, false, false, false, true, true, false};

更新 6 至其邻接节点的距离；

• distSet = {0, 4, 12, INF, INF, 11, 9, 8, 15};

以此类推，直到遍历结束。

• sptSet = {true, true, true, true, true, true, true, true, true};
• distSet = {0, 4, 12, 19, 21, 11, 9, 8, 14};

最终结果为源顶点 0 至所有顶点的距离：

Vertex   Distance from Source
0                0
1                4
2                12
3                19
4                21
5                11
6                9
7                8
8                14

C#代码实现：

  1 using System;
  2 using System.Collections.Generic;
  3 using System.Linq;
  4 
  5 namespace GraphAlgorithmTesting
  6 {
  7   class Program
  8   {
  9     static void Main(string[] args)
 10     {
 11       int[,] graph = new int[9, 9]
 12       {
 13         {0, 4, 0, 0, 0, 0, 0, 8, 0},
 14         {4, 0, 8, 0, 0, 0, 0, 11, 0},
 15         {0, 8, 0, 7, 0, 4, 0, 0, 2},
 16         {0, 0, 7, 0, 9, 14, 0, 0, 0},
 17         {0, 0, 0, 9, 0, 10, 0, 0, 0},
 18         {0, 0, 4, 0, 10, 0, 2, 0, 0},
 19         {0, 0, 0, 14, 0, 2, 0, 1, 6},
 20         {8, 11, 0, 0, 0, 0, 1, 0, 7},
 21         {0, 0, 2, 0, 0, 0, 6, 7, 0}
 22       };
 23 
 24       Graph g = new Graph(graph.GetLength(0));
 25       for (int i = 0; i < graph.GetLength(0); i++)
 26       {
 27         for (int j = 0; j < graph.GetLength(1); j++)
 28         {
 29           if (graph[i, j] > 0)
 30             g.AddEdge(i, j, graph[i, j]);
 31         }
 32       }
 33 
 34       int[] dist = g.Dijkstra(0);
 35       Console.WriteLine("Vertex\t\tDistance from Source");
 36       for (int i = 0; i < dist.Length; i++)
 37       {
 38         Console.WriteLine("{0}\t\t{1}", i, dist[i]);
 39       }
 40 
 41       Console.ReadKey();
 42     }
 43 
 44     class Edge
 45     {
 46       public Edge(int begin, int end, int distance)
 47       {
 48         this.Begin = begin;
 49         this.End = end;
 50         this.Distance = distance;
 51       }
 52 
 53       public int Begin { get; private set; }
 54       public int End { get; private set; }
 55       public int Distance { get; private set; }
 56     }
 57 
 58     class Graph
 59     {
 60       private Dictionary<int, List<Edge>> _adjacentEdges
 61         = new Dictionary<int, List<Edge>>();
 62 
 63       public Graph(int vertexCount)
 64       {
 65         this.VertexCount = vertexCount;
 66       }
 67 
 68       public int VertexCount { get; private set; }
 69 
 70       public void AddEdge(int begin, int end, int distance)
 71       {
 72         if (!_adjacentEdges.ContainsKey(begin))
 73         {
 74           var edges = new List<Edge>();
 75           _adjacentEdges.Add(begin, edges);
 76         }
 77 
 78         _adjacentEdges[begin].Add(new Edge(begin, end, distance));
 79       }
 80 
 81       public int[] Dijkstra(int source)
 82       {
 83         // dist[i] will hold the shortest distance from source to i
 84         int[] distSet = new int[VertexCount];
 85 
 86         // sptSet[i] will true if vertex i is included in shortest
 87         // path tree or shortest distance from source to i is finalized
 88         bool[] sptSet = new bool[VertexCount];
 89 
 90         // initialize all distances as INFINITE and stpSet[] as false
 91         for (int i = 0; i < VertexCount; i++)
 92         {
 93           distSet[i] = int.MaxValue;
 94           sptSet[i] = false;
 95         }
 96 
 97         // distance of source vertex from itself is always 0
 98         distSet[source] = 0;
 99 
100         // find shortest path for all vertices
101         for (int i = 0; i < VertexCount - 1; i++)
102         {
103           // pick the minimum distance vertex from the set of vertices not
104           // yet processed. u is always equal to source in first iteration.
105           int u = CalculateMinDistance(distSet, sptSet);
106 
107           // mark the picked vertex as processed
108           sptSet[u] = true;
109 
110           // update dist value of the adjacent vertices of the picked vertex.
111           for (int v = 0; v < VertexCount; v++)
112           {
113             // update dist[v] only if is not in sptSet, there is an edge from 
114             // u to v, and total weight of path from source to  v through u is 
115             // smaller than current value of dist[v]
116             if (!sptSet[v]
117               && distSet[u] != int.MaxValue
118               && _adjacentEdges[u].Exists(e => e.End == v))
119             {
120               int d = _adjacentEdges[u].Single(e => e.End == v).Distance;
121               if (distSet[u] + d < distSet[v])
122               {
123                 distSet[v] = distSet[u] + d;
124               }
125             }
126           }
127         }
128 
129         return distSet;
130       }
131 
132       /// <summary>
133       /// A utility function to find the vertex with minimum distance value, 
134       /// from the set of vertices not yet included in shortest path tree
135       /// </summary>
136       private int CalculateMinDistance(int[] distSet, bool[] sptSet)
137       {
138         int minDistance = int.MaxValue;
139         int minDistanceIndex = -1;
140 
141         for (int v = 0; v < VertexCount; v++)
142         {
143           if (!sptSet[v] && distSet[v] <= minDistance)
144           {
145             minDistance = distSet[v];
146             minDistanceIndex = v;
147           }
148         }
149 
150         return minDistanceIndex;
151       }
152     }
153   }
154 }

参考资料

• 广度优先搜索
• Dijkstra's algorithm
• Greedy Algorithms | Set 7 (Dijkstra’s shortest path algorithm)
• Bellman-Ford 单源最短路径算法
• Introduction to Algorithms 6.006 - Lecture 16

本篇文章《Dijkstra 单源最短路径算法》由 Dennis Gao 发表自博客园，未经作者本人同意禁止任何形式的转载，任何自动或人为的爬虫转载行为均为耍流氓。