关于后缀数组的倍增算法和height数组
自己看着大牛的论文学了一下后缀数组,看了好久好久,想了好久好久才懂了一点点皮毛TAT
然后就去刷传说中的后缀数组神题,poj3693是进化版的,需要那个相同情况下字典序最小,搞这个搞了超久的说。
先简单说一下后缀数组。首先有几个重要的数组:
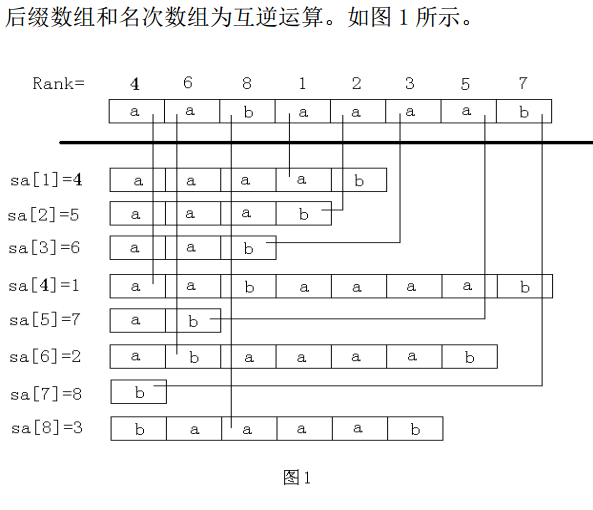
·SA数组(后缀数组):保存所有后缀排序后从小到大的序列。[即SA[i]=j表示排名第i的后缀编号为j]
·rank数组(名次数组):记录后缀的名次。[即rank[i]=j表示编号为i的后缀排名第j]
用倍增算法可以在O(nlogn)时间内得出这两个数组。
具体过程如下:
即每次长度增加一倍,直接用前面算出的排名作为关键字,问题转化为给有两个关键字的序列排序,这里可以用基数排序,每次排序时间为n,一共进行了logn次,所以总共时间复杂度为O(nlogn)。要注意如果一个字符串包含另一个字符串,长度小的较小,那就是说如果没有第二关键字,把第二关键字默认为0即可。具体如下:
数组y保存的是对第二关键字排序的结果
数组wr保存的是对第二关键字排序后的rank值
ln为当前子串的长度
rank值为排名,在这里即为关键字的值
排序时如果两个关键字相同即默认位置前的较小,那么我们先按照第二关键字排序,再按照第一关键字排序,最后排出来的就是第一第二关键字合并的结果(基数排序的方法)
下一步是计算新的rank值。这里要注意的是,可能有多个字符串的rank值是相同的,所以必须比较两个字符串是否完全相同,wr数组的值已经没有必要保存,为了节省空间,这里用wr数组保存rank值。
一直做到所有后缀的排名不同结束,时间复杂度为O(nlogn)。
后缀数组的大部分应用都跟一个很重要的height数组有关。
height数组定义:定义height[i]=suffix(sa[i-1])和suffix(sa[i])的最长公共前缀,也就是排名相邻的两个后缀的最长公共前缀。
对于j和k,不妨设rank[j]<rank[k],则有以下性质:
suffix(j)和suffix(k)的最长公共前缀为:
height[rank[j]+1], height[rank[j]+2], height[rank[j]+3], …, height[rank[k]]中的最小值。
h数组有以下性质: h[i]≥h[i-1]-1
证明:
设suffix(k)是排在suffix(i-1)前一名的后缀,则它们的最长公共前缀是h[i-1]。那么suffix(k+1)将排在suffix(i)的前面(这里要求h[i-1]>1,如果h[i-1]≤1,原式显然成立)并且suffix(k+1)和suffix(i)的最长公共前缀是h[i-1]-1,所以suffix(i)和在它前一名的后缀的最长公共前缀至少是h[i-1]-1。因此得证。(如图)
按照h[1],h[2],……,h[n]的顺序计算,并利用h数组的性质,时间复杂度可以降为O(n)。
实现的时候其实没有必要保存h数组,只须按照h[1],h[2],……,h[n]的顺序计算即可。
标程如下:
1 #include<cstdio> 2 #include<cstdlib> 3 #include<cstring> 4 #include<iostream> 5 #define Maxn 11000 6 using namespace std; 7 8 int sa[Maxn],rank[Maxn],y[Maxn],Rsort[Maxn]; 9 int wr[Maxn],n,a[Maxn],height[Maxn]; 10 11 //cmp 第一关键字且第二关键字相同 12 bool cmp(int k1,int k2,int ln){return wr[k1]==wr[k2] && wr[k1+ln]==wr[k2+ln];} 13 int mymax(int x,int q) {return x>q?x:q;} 14 15 void get_sa(int m) //构建SA后缀数组 16 { 17 int i,k,p,ln; 18 19 memcpy(rank,a,sizeof(rank)); 20 //a数组:原字符串,rank名次数组 21 22 for (i=0;i<=m;i++) Rsort[i]=0; 23 for (i=1;i<=n;i++) Rsort[rank[i]]++; 24 for (i=1;i<=m;i++) Rsort[i]+=Rsort[i-1]; 25 for (i=n;i>=1;i--) sa[Rsort[rank[i]]--]=i; 26 //以上四句为基数排序,不懂的看flash 27 28 ln=1; p=0; 29 // ln为当前子串的长度,p表示有多少不相同的子串 30 while (p<n) 31 { 32 for (k=0,i=n-ln+1;i<=n;i++) y[++k]=i; 33 for (i=1;i<=n;i++) if (sa[i]>ln) y[++k]=sa[i]-ln; 34 for (i=1;i<=n;i++) wr[i]=rank[y[i]];//在这里rank表示一个值 35 //数组y保存的是对第二关键字排序的结果(2-sa)。 36 //数组wr保存的是对第二关键字排序后的rank值(rank即第一关键字) 37 //wr[i]->第二关键字排名为i的第一关键字的值 38 //以下为对第一关键字排序 39 for (i=0;i<=m;i++) Rsort[i]=0; 40 for (i=1;i<=n;i++) Rsort[wr[i]]++; 41 for (i=1;i<=m;i++) Rsort[i]+=Rsort[i-1]; 42 for (i=n;i>=1;i--) sa[Rsort[wr[i]]--]=y[i]; 43 44 45 memcpy(wr,rank,sizeof(wr)); 46 p=1; rank[sa[1]]=1; 47 for (i=2;i<=n;i++) 48 { 49 if (!cmp(sa[i],sa[i-1],ln)) p++; 50 rank[sa[i]]=p; 51 } 52 //得到新的rank数组 53 m=p; ln*=2;//m个rank ln长度 54 } 55 a[0]=0; sa[0]=0; 56 } 57 58 void get_he() 59 { 60 int i,j,kk=0; 61 //height[i]表示排名为i的子串和比起前一位排名的子串的最长公共前缀 62 for (i=1;i<=n;i++) //目前求的是位置为i的子串的height值 63 { 64 j=sa[rank[i]-1]; 65 if (kk) kk--; 66 67 while (a[j+kk]==a[i+kk]) kk++; 68 height[rank[i]]=kk; 69 } 70 } 71 72 int main() 73 { 74 int i,m=-1; 75 char c; 76 n=0; 77 while(1) 78 { 79 scanf("%c",&c); 80 if(c=='\n') break; 81 a[++n]=c-'a'; 82 } 83 for (i=1;i<=n;i++) 84 m=mymax(m,a[i]); 85 get_sa(m+10); 86 for(i=1;i<=n;i++) 87 printf("%d ",sa[i]); 88 89 }