【poj3693】Maximum repetition substring（后缀数组+RMQ）

 

　　题意：给定一个字符串，求重复次数最多的连续重复子串。
　　

　　传说中的后缀数组神题，蒟蒻真的调了很久才对啊。感觉对后缀数组和RMQ的模版都不是很熟，导致还是会有很多各种各样的小错误= =

 

　　首先，枚举重复子串的循环节为L，因为枚举的是循环节长度，所以是没有单调性的，那么枚举就要用0(n)的时间了。连续一次的情况是可以的，所以这里只考虑重复两次或以上的情况。

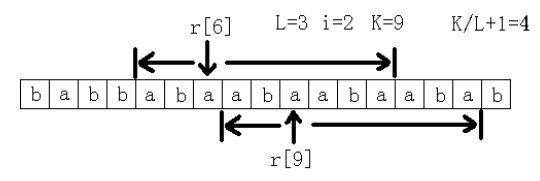
　　记这个连续重复子串为L，我们可以发现，这个字符串一定会覆盖s[0],s[L],s[L*2].....这些点中相邻的两个（因为长度至少为2L嘛）。假设它覆盖的是s[L*i]和s[L*(i+1)]，那么我们就往前和往后计算能匹配多远（往后匹配用到了后缀数组的height数组，往前匹配可以while到s[L*(i-1)]，越过s[L*(i-1)]的情况和前面计算的重复了，可以不算）

　　记往前匹配和往后匹配的最长长度为k，则重复次数为k/L+1。(如图)

 

 

 

　　穷举长度L的时间为n，每次计算的时间为n/L。

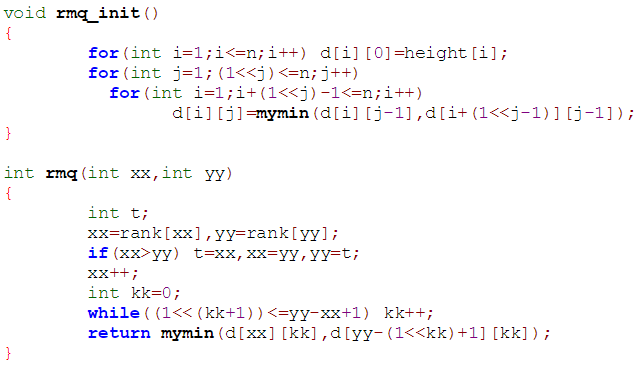
　　另外，要在较快的时间内求出以i为开头的后缀和以j为开头的后缀的最长公共前缀要用到RMQ。即快速算出min(height[rank[i]]~height[rank[j]])。用rmq[i][j]表示i~i+(1<<j)-1的min(height)，具体如下。

 

代码如下：

  1 #include<cstdio>
  2 #include<cstdlib>
  3 #include<cstring>
  4 #include<iostream>
  5 #include<algorithm>
  6 using namespace std;
  7 #define Maxn 100100
  8 
  9 char s[Maxn];
 10 int a[Maxn],n;
 11 int rank[Maxn],sa[Maxn],Rsort[Maxn],y[Maxn],wr[Maxn];
 12 int height[Maxn],d[Maxn][20],ans[Maxn],as[Maxn],al;
 13 int maxx,pos,len;
 14 
 15 int mymin(int xx,int yy) {return xx<yy?xx:yy;}
 16 
 17 void get_sa(int m)
 18 {
 19     memcpy(rank,a,sizeof(rank));
 20     for(int i=0;i<=m;i++) Rsort[i]=0;
 21     for(int i=1;i<=n;i++) Rsort[rank[i]]++;
 22     for(int i=1;i<=m;i++) Rsort[i]+=Rsort[i-1];
 23     for(int i=n;i>=1;i--) sa[Rsort[rank[i]]--]=i;
 24     
 25     int ln=1,p=0;
 26     while(p<n)
 27     {
 28         int k=0;
 29         for(int i=n-ln+1;i<=n;i++) y[++k]=i;
 30         for(int i=1;i<=n;i++) if(sa[i]>ln) y[++k]=sa[i]-ln;
 31         for(int i=1;i<=n;i++) wr[i]=rank[y[i]];
 32         
 33         for(int i=0;i<=m;i++) Rsort[i]=0;
 34         for(int i=1;i<=n;i++) Rsort[wr[i]]++;
 35         for(int i=1;i<=m;i++) Rsort[i]+=Rsort[i-1];
 36         for(int i=n;i>=1;i--) sa[Rsort[wr[i]]--]=y[i];
 37         
 38         memcpy(wr,rank,sizeof(wr));
 39         p=1;rank[sa[1]]=1;
 40         for(int i=2;i<=n;i++)
 41         {
 42             if(wr[sa[i]]!=wr[sa[i-1]]||wr[sa[i]+ln]!=wr[sa[i-1]+ln]) p++;
 43             rank[sa[i]]=p;
 44         }
 45         m=p,ln*=2;
 46     }
 47     sa[0]=rank[0]=0;
 48 }
 49 
 50 void get_he()
 51 {
 52     int kk=0;
 53     for(int i=1;i<=n;i++)
 54     {
 55         int j=sa[rank[i]-1];
 56         if(kk) kk--;
 57         while(a[i+kk]==a[j+kk]) kk++;
 58         height[rank[i]]=kk;
 59     }
 60 }
 61 
 62 void rmq_init()
 63 {
 64     for(int i=1;i<=n;i++) d[i][0]=height[i];
 65     for(int j=1;(1<<j)<=n;j++)
 66       for(int i=1;i+(1<<j)-1<=n;i++)
 67         d[i][j]=mymin(d[i][j-1],d[i+(1<<j-1)][j-1]);
 68 }
 69 
 70 int rmq(int xx,int yy)
 71 {
 72     int t;
 73     xx=rank[xx],yy=rank[yy];
 74     if(xx>yy) t=xx,xx=yy,yy=t;
 75     xx++;
 76     int kk=0;
 77     while((1<<(kk+1))<=yy-xx+1) kk++;
 78     return mymin(d[xx][kk],d[yy-(1<<kk)+1][kk]);
 79 }
 80 
 81 void ffind()
 82 {
 83     al=0;
 84     maxx=1;
 85     for(int i=1;i<=n/2;i++)
 86       for(int j=1;j+i<=n;j+=i)
 87       {
 88           if(a[j]!=a[j+i]) continue;
 89           int kk=rmq(j,j+i),now,r;
 90           now=kk/i+1;r=i-kk%i;
 91           //if(now>maxx) maxx=now,ans[al=1]=j,as[al]=i;
 92           //else if(now==maxx) ans[++al]=j,as[al]=i;
 93           int cnt=0,p=j;
 94           for(int m=j-1;m>j-i&&a[m]==a[m+i]&&m;m--)
 95           {
 96               cnt++;
 97               if(cnt==r) now++,p=m;
 98               else p=rank[p]>rank[m]?m:p;
 99           }
100           if(now>maxx) maxx=now,pos=p,len=i;
101           else if(now==maxx&&rank[pos]>rank[p]) pos=p,len=i;
102       }
103 }
104 
105 bool cp(int f1,int a1,int f2,int a2)
106 {
107     int kk=rmq(f1,f2);
108     if(kk>=a1-1&&kk>=a2-1) return a1<=a2?0:1;
109     if(kk>=a1-1) return 1;if(kk>=a2-1) return 0;
110     return a[f1+kk]>a[f2+kk];
111 }
112 
113 int main()
114 {
115     int kase=0;
116     while(1)
117     {
118         scanf("%s",s+1);
119         if(s[1]=='#') break;
120         n=strlen(s+1);int minn=100;
121         memset(a,0,sizeof(a));
122         for(int i=1;i<=n;i++)
123         {
124             a[i]=s[i]-'a'+1;
125             minn=mymin(minn,a[i]);
126         }
127         get_sa(30);
128         get_he();
129         rmq_init();
130         ffind();
131         printf("Case %d: ",++kase);
132         if(maxx==1) printf("%c",minn+'a'-1);
133         else
134         {
135             for(int i=pos;i<=pos+len*maxx-1;i++) printf("%c",s[i]);
136         }
137         printf("\n");
138     }
139     return 0;
140 }

poj3693

 

2015-12-15 17:02:11