两点间所有路径的遍历算法
转自:http://blog.sina.com.cn/s/blog_5ff8e88e01013lot.html
这几天,用到了这个功能,但在网上找到了一份资料,思路写的很清晰,但代码有错误。因此,我就按着这个思路,自己整理了代码,现在说明如下:(引用前部分思想,更新后部分代码)
两点间所有路径的遍历算法
中国海洋大学 信息科学与工程学院 熊建设 梁磊
摘要:本文首先简单介绍图的深度优先遍历算法,接着根据图的深度优先遍历算法求出连通图中两点间所有路径,并给出代码。
关键词:图、深度优先遍历、算法
Abstract:This arcicle introduces the Depth-First Traversal method,then introduces an algorithm to find all roads from one point to another point in a simple graph,and gives the codes with C++.
Key Words:Graph、 Algorithm
一、深度优先遍历(Depth-First Traversal)
1.图的深度优先遍历的递归定义
假设给定图G的初态是所有顶点均未曾访问过。在G中任选一顶点v为初始出发点(源点),则深度优先遍历可定义如下:首先访问出发点v,并将其标记为已访问过;然后依次从v出发搜索v的每个邻接点w。若w未曾访问过,则以w为新的出发点继续进行深度优先遍历,直至图中所有和源点v有路径相通的顶点(亦称为从源点可达的顶点)均已被访问为止。若此时图中仍有未访问的顶点,则另选一个尚未访问的顶点作为新的源点重复上述过程,直至图中所有顶点均已被访问为止。
图的深度优先遍历类似于树的前序遍历。采用的搜索方法的特点是尽可能先对纵深方向进行搜索。这种搜索方法称为深度优先搜索(Depth-First Search)。相应地,用此方法遍历图就很自然地称之为图的深度优先遍历。
2、深度优先搜索的过程
设x是当前被访问顶点,在对x做过访问标记后,选择一条从x出发的未检测过的边(x,y)。若发现顶点y已访问过,则重新选择另一条从x出发的未检测过的边,否则沿边(x,y)到达未曾访问过的y,对y访问并将其标记为已访问过;然后从y开始搜索,直到搜索完从y出发的所有路径,即访问完所有从y出发可达的顶点之后,才回溯到顶点x,并且再选择一条从x出发的未检测过的边。上述过程直至从x出发的所有边都已检测过为止。此时,若x不是源点,则回溯到在x之前被访问过的顶点;否则图中所有和源点有路径相通的顶点(即从源点可达的所有顶点)都已被访问过,若图G是连通图,则遍历过程结束,否则继续选择一个尚未被访问的顶点作为新源点,进行新的搜索过程。
二、求两点间所有路径的算法
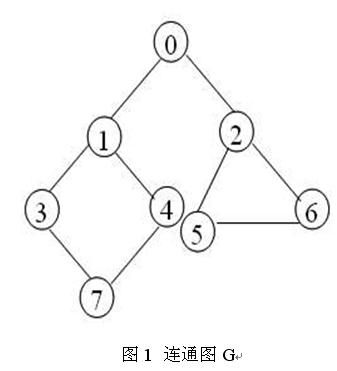
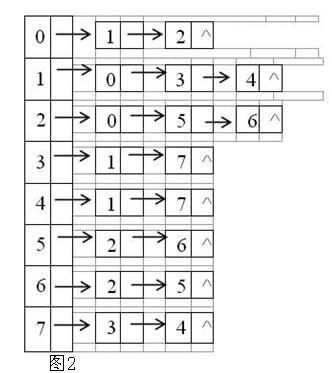
假设简单连通图如图1所示,那么它的邻接表存储结构如图2所示。假设我们要找出结点3到结点6的所有路径,那么,我们就设结点3为起点,结点6为终点。我们需要的存储结构有:一个保存路径的栈、一个保存已标记结点的数组,那么找到结点3到结点6的所有路径步骤如下:
1、 我们建立一个存储结点的栈结构,将起点3入栈,将结点3标记为入栈状态;
2、 从结点3出发,找到结点3的第一个非入栈状态的邻结点1,将结点1标记为入栈状态;
3、 从结点1出发,找到结点1的第一个非入栈状态的邻结点0,将结点0标记为入栈状态;
4、 从结点0出发,找到结点0的第一个非入栈状态的邻结点2,将结点2标记为入栈状态;
5、 从结点2出发,找到结点2的第一个非入栈状态的邻结点5,将结点5标记为入栈状态;
6、 从结点5出发,找到结点5的第一个非入栈状态的邻结点6,将结点6标记为入栈状态;
7、 栈顶结点6是终点,那么,我们就找到了一条起点到终点的路径,输出这条路径;
8、 从栈顶弹出结点6,将6标记为非入栈状态;
9、 现在栈顶结点为5,结点5没有除终点外的非入栈状态的结点,所以从栈顶将结点5弹出;
10、 现在栈顶结点为2,结点2除了刚出栈的结点5之外,还有非入栈状态的结点6,那么我们将结点6入栈;
11、 现在栈顶为结点6,即找到了第二条路径,输出整个栈,即为第二条路径
12、 重复步骤2-11,就可以找到从起点3到终点6的所有路径;
13、 栈为空,算法结束。
三、算法C++代码如下:
#include <iostream>
#include <map>
using namespace std;
class node
{
public:
int number;
node *next;
node(int a,node *b)
{
number=a;
next=b;
}
};
class stacks
{
public:
node * top;
stacks(node * a=NULL)
{
top=NULL;
}
void push(int a)
{
if (top==NULL)
top =new node(a,NULL);
else top=new node(a,top);
}
void pop()
{
node *b=top;
top=top->next;
delete b;
}
}; //保存已加入路径结点的栈
int cur_node;//当前结点,即为栈顶的结点
int next_node=8 ;//当前结点的下一个邻接点,即刚从栈顶弹出的结点,初始化为8
map<int,int> map_next;//每个结点的下一个邻接点,即刚从栈顶弹出的结点
int start=3;
int end=6;//起点为3,终点为6
stacks aray[8]={stacks(NULL),stacks(NULL),stacks(NULL),stacks(NULL),stacks(NULL),stacks(NULL),stacks(NULL),stacks(NULL)};
stacks stack(NULL);
int states[8];//保存结点状态的数组
int main()
{
//初始化map_next
for(int i=0;i<=7;i++)
{
map_next[i] = -1;
}
aray[0].push(2);
aray[0].push(1);
aray[1].push(4);
aray[1].push(3);
aray[1].push(0);
aray[2].push(6);
aray[2].push(5);
aray[2].push(0);
aray[3].push(7);
aray[3].push(1);
aray[4].push(7);
aray[4].push(1);
aray[5].push(6);
aray[5].push(2);
aray[6].push(5);
aray[6].push(2);
aray[7].push(4);
aray[7].push(3);
node* neighbour(int a);// ,int b
stack.push(start);//将起点入栈
states[start]=1;//将起点标记为入栈状态
while(NULL != stack.top) //栈不为空
{
if (stack.top->number==end)
{
cout<<"end";
node* abc=stack.top;
while(abc->number != start)
{
cout<<abc->number<<",";
abc=abc->next;
}
cout << "start"<<endl;//输出已找到的路径
stack.pop();//将栈顶结点弹出
states[end]=0;//清除终点的状态
map_next[end]=-1;
}
else
{
cur_node=stack.top->number;
if(neighbour(cur_node) != NULL)//邻居不为空
{
node *d =neighbour(cur_node);
map_next[cur_node] = d->number;
cur_node=d->number;
stack.push(cur_node);
states[cur_node]=1;
}
else
{
stack.pop();
states[cur_node]=0;
map_next[cur_node] = -1;
}
}
}
return 0;
}
node* neighbour(int a)//,int b
{
node *abc=aray[a].top;
while ((NULL!=abc))//结点abc不空
{
if( states[abc->number]==1 )//已经在栈stack里了
{
abc=abc->next;
}
else//不在栈stack里
{
if(-1 == map_next[a])//就要abc作为返回值
{
while(NULL!=abc && states[abc->number]==1)
{
abc = abc->next;
}
return abc;
}
else if(abc->number == map_next[a])
{
abc=abc->next;
while(NULL!=abc && states[abc->number]==1)
{
abc = abc->next;
}
return abc; //将abc的下一个结点返回
}
else
{
abc=abc->next;
}
}
}
return NULL;
}
四、总结
本算法利用无向图的邻接表存储结构,通过深度优先遍历来查找连通图中两点间所有路径。算法并不复杂,效率较高。由于有向图也可以用邻接表来存储,所以该算法对于有向图也是适用的。
五,参考文献
[1] 严蔚敏,吴伟民. 数据结构(C 语言版) [M] . 北京:清华大学出版杜,1997
[2] 谭浩强 C++面向对象程序设计 北京:清华大学出版杜,2006
[3] Larry Nyhoff黄达明 数据结构与算法分析:C++语言描述 清华大学出版社 2006