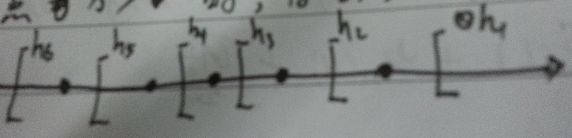Foundations of Machine Learning: Rademacher complexity and VC-Dimension(2)
Foundations of Machine Learning: Rademacher complexity and VC-Dimension(2)
(一) 增长函数(Growth function)
在引入增长函数之前,我们先介绍一个例子,这个例子会有助于理解增长函数这个东西。
在input space为$\mathbb{R}$,假设空间为阈值函数,即当输入的点$x>v$时,将该点标为正。如 图1 为其中的6个假设。
图1 阈值函数示例
很显然,这个假设集合的大小为无限多个。但实际,我们很容易发现,对一个样本大小为m的样本,这些假设集可以分成$m+1$个大类,而每个大类里的假设对该样本产生的经验错都是一致的。故我们很容易的想到可以直接用每个大类的一个假设作为代表,也就是说无限个假设实际上有效的假设只有$m+1$个。所以第一,第二篇文章中的$|H|$可以用$m+1$来代替。
但很不幸,这是一个特定的例子,并且有效函数依赖与样本,所以我们并不容易将其推广开来。但换个思维,我们是否可以找到某种方法将无限多的假设集分成有限个大类,即用有限个有效的假设集来等价这个无限个假设集。这就是增长函数要干的事。
首先,定义一个二分的集合:
$$\Pi_H(S)=\{(h(x_1),...,h(x_m)):h\in H\}$$
每一个$h$对样本进行二分类,都会得到一个结果,所有的结果形成的集合即$\Pi_H(S)$,显然$|\Pi_H(S)|\leq 2^m$。
定义 2.3 增长函数 对一个假设集合H的增长函数$\Pi_H:N\rightarrow N$ 定义为:
$$\forall m\in N,\Pi_H(m)=\max _{s\in \mathcal{X}^m}\mid \Pi_H(S)\mid$$
$\Pi_H(m)$表示使用hypothesis H 对任意m个点进行分类所能够产生的最大数量的不同方法。增长函数提供了另外一种衡量hypothesis set H 复杂性的方法,并且这种方法与 Rademacher complexity 不一样,它不依赖于产生样本的分布。
首先,我们先介绍一下Hoeffding引理。
Hoeffding Lemma: 令$a\leq X\leq b$为期望$E[X]=0$的随机变量。那么,对于所有$t>0$,以下不等式成立:
$$E[exp(tX)] \leq exp(\frac{t^2(b-a)^2}{8})$$
定理 2.3 Massart's lemma: 令$A\in \mathbb{R}^m$为一个有限的集合,记$r=\max_{X\in A}\parallel X\parallel_2$,那么以下不等式成立:
$$\mathop{E} _{\delta}[\frac{1}{m} \sup _{x\in A}\sum_{i=1}^m \sigma_ix_i]\leq\frac{r\sqrt{2log\mid A\mid}}{m}.$$
这里的$\sigma_i$为取值为$\{+1,-1\}$的独立均匀随机变量,$x_1,...,x_m$ 为向量$x$的各个成分。
证明: 对任意$t>0$,使用Jensen's 不等式可得:
\begin{align*}\exp(t\mathop{E} _\sigma[\sup _{x\in A}\sum _{i=1} ^m\sigma_ix_i])&\leq \mathop{E} _\sigma[\exp(t\sup _{x\in A}\sum _{i=1} ^m\sigma_ix_i)] \\&= \mathop{E} _\sigma[\sup _{x\in A}\exp(\sum _{i=1} ^mt\sigma_ix_i)] \\&\leq \sum _{x\in A}\mathop{E} _\sigma[\exp(\sum _{i=1} ^mt\sigma_ix_i)] \end{align*}
再根据$\sigma_i$的独立性,应用Hoeffding's lemma可得:
\begin{align*}\exp(t\mathop{E} _\sigma[\sup _{x\in A}\sum _{i=1} ^m\sigma_ix_i])&\leq \sum _{x\in A}\prod _{i=1} ^m\mathop{E} _{\sigma_i}[\exp(t\sigma_ix_i)] \\&\leq \sum _{x\in A}\prod _{i=1} ^m \exp[\frac{t^2(2x_i)^2}{8}] \\&=\sum _{x\in A}exp[\frac{t^2}{2}\sum _{i=1} ^mx_i^2] \\&\leq \sum _{x\in A}exp[\frac{t^2r^2}{2}]=|A|e^{\frac{t^2r^2}{2}}\end{align*}
两边取$\log$,再同时除以t,可得:
$$\mathop{E} _{\sigma}[\sup _{x\in A}\sum_{i=1}^m \sigma_i x_i] \leq \frac{\log|A|}{t}+\frac{tr^2}{2}$$
对所有$t>0$均成立,令$t=\frac{\sqrt{2\log|A|}}{r}$,使右边的式子最小,
$$\mathop{E} _{\delta}[\mathop{sup} _{x\in A}\sum_{i=1}^m \sigma_i x_i] \leq r\sqrt{2\log|A|}$$
再同时除以m即得到定理中的式子。证毕!
应用Massart's lemma,就可以用增长函数界定Rademacher complexity.
推论 2.1 令G为取值为$\{+1,-1\}$的函数族,那么以下不等式成立:
$$\mathfrak{R}_m(G)\leq\sqrt{\frac{2log\Pi_G(m)}{m}}.$$
证明: 对一个固定的样本$S=(x_1,...,x_m)$,定义$G_{|S}$为
$$G_{|S}=\{ (g(x_1),...,g(x_m)))^T:g\in G \}$$
由于$g(x)$的取值为$\{-1,1\}$,所以对$\forall u\in G_{|S}$,有$\| u\|_2\leq \sqrt{m}$。并且根据$G_{|S}$定义可知$G_{|S}=\Pi_G(S)$,故$|G_{|S}|\leq \Pi_G(m)$。
所以,应用Massart's lemma有:
\begin{align*}\mathfrak{R}_m(G) &= \mathop{E} _S[\mathop{E} _\sigma[\sup _{u\in G_{|S}}\frac{1}{m}\sum _{i=1} ^m\sigma_iu_i]] \\&\leq \mathop{E} _S[\frac{\sqrt{m}\sqrt{2\log|G_{|S}|}}{m}] \\&\leq \mathop{E} _S[\frac{\sqrt{m}\sqrt{2\log\Pi_G(m)}}{m}] \leq \sqrt{\frac{2\log\Pi_G(m)}{m}}\end{align*}
证毕!
再将它与 定理2.2 结合起来,就得到增长函数表示的泛化边界:
推论 2.2 增长函数泛化界 令H为取值为$\{-1,+1\}$的函数族。那么,对任意$\delta>0$,以概率$1-\delta$,对所有$h\in H$,以下不等式成立:
\begin{align}\label{equ:9}R(h)\leq\widehat{R}(h)+\sqrt{\frac{2log\Pi_H(m)}{m}}+\sqrt{\frac{log\frac{1}{\delta}}{2m}}\end{align}
另外,增长函数也可以不用首先通过Rademacher Complexity来界定,即:
$$\mathop{Pr}[\mid R(h)-\widehat{R}(h)\mid>\epsilon]\leq 4\Pi_H(2m)exp(-\frac{m\epsilon^2}{8})$$
这个不等式与式子\ref{equ:9}只差一个常数。
(二)VC维(VC-Dimension)
在介绍VC维时,我们得先来了解二个概念,一个是前面在介绍增长函数时已经讲过的“二分”(dichotomy),还有一个是打散(shattering)。
所谓“二分”指的是给定一个样本S,和一个假设$h$,用$h$对S进行分类的结果称为二分。因此对一个假设集合H,可以产生多种不同的“二分”,而这些二分构成了假设集H对样本S的二分集合$\Pi_H(S)$。
“打散”的概念同样也是针对假设集和样本。我们说“一个样本S可以被假设集H打散”当且仅当用这个假设集中的假设可以实现样本S的所有可能的“二分”,即$\mid \Pi_H(S)\mid=2^m$。
现在来定义VC维,假设集H的VC维指的就是能够被H打散的最大的样本个数。更严格定义如下:
定义 2.4 VC-Dimension 假设集H的VC维是能够被H打散的最大样本集的大小:
$$\mathop{VCdim}(H)=\max{m:\Pi_H(m)=2^m}.$$
这里必须注意两点:如果我们说假设集H的VC维d,那么意思就是说
- 存在着一个样本大小为d的样本能够被H打散(并不是说所有样本大小为d的样本都能够被打散);
- 不存在一个样本大小为$d+1$的样本能够被H打散(即所有样本大小为$d+1$的样本都不能被H打散)
一些例子(这些例子的证明可见本人以前的文章:http://www.cnblogs.com/boostable/p/iage_VC_dimension.html):
- 当S为平面,H为矩形框,$VCdim(H)=4$.
- 当S为x轴,H为区间,$VCdim(H)=2$.
- 当S为圆周,H为凸集,$VCdim(H)=\infty$.
- 当S为k维空间,H为半空间,$VCdim(H)=k+1$.
接下来我们来证明一个定理,它将增长函数与VC维联系起来。
定理 2.4 Sauer's lemma 令H称为$\mathop{VCdim}(H)=d$的假设集。那么,对所有$m\in N$,以下不等式成立:
$$\Pi_H(m)\leq\sum_{i=0}^d{m \choose i}.$$
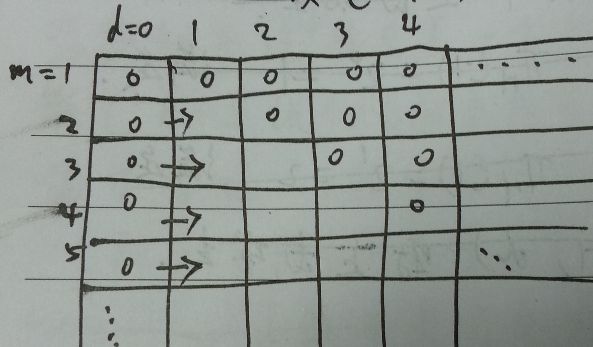
证明:首先,确定m可取的值为$1,2,...$,d可取的值为$0,1,2,...$,
- 当$m=d$时,$\Pi_H(m)=2^d$,而
$$\sum _{i=0} ^d {m \choose i}=\sum _{i=0} ^d{d \choose i}=2^d$$
故上式成立。 - 当$m<d$时,$\Pi_H(m)=2^m$,而
$$\sum _{i=0} ^d {m \choose i}=\sum _{i=0} ^m{m \choose i}+\sum _{i=m+1} ^d{m \choose i}=2^m $$
故上式成立。 - 当$m>d$时,用归纳法证明。
- 当$d=0$时,对所有m都成立。这是因为$d=0$时$\Pi_H(m)=2^0$,而$\sum _{i=0} ^d{m \choose i}=1$,故成立。
- 假设$(m,d-1)$时成立,即$\Pi_H(m)\leq\sum _{i=0} ^{d-1}{m \choose i}$,则
$$\sum _{i=0} ^{d-1}{m \choose i} \leq \sum _{i=0} ^{d-1}{m \choose i}+{m \choose d}=\sum _{i=0} ^{d}{m \choose i}$$
$(m,d)$也成立。
如 图2 所示。证毕!
图2 Sauer's lemma 示例
推论 2.3 令H为$\mathop{VCdim}(H)=d$的假设集。那么,对所有的$m\geq d$:
$$\Pi_H(m)\leq{\frac{em}{d}}^d=O(m^d)$$
证明:
\begin{align*}\Pi_H(m) &\leq \sum _{i=0} ^d {m \choose i} \\&\leq \sum _{i=0} ^d {m \choose i}(\frac{m}{d})^{d-i} \\&\leq \sum _{i=0} ^m {m \choose i}(\frac{m}{d})^{d-i} \\&=(\frac{m}{d})^d\sum _{i=0} ^m{m \choose i}(\frac{m}{d})^i \\&=(\frac{m}{d})^d(1+\frac{d}{m})^m \leq (\frac{m}{d})^de^d\end{align*}
最后一个不等式是因为$(1-x)\leq e^{-x}$。证毕!
于是我们可以把推论2.2 中的$\Pi_H(m)$用它的上界$(\frac{em}{d})^d$来替代,得到如下推论:
推论 2.4 VC-维泛化界 令H为取值为$\{+1,-1\}$且VC维为d的假设集。那么,对任意的$\delta>0$,至少以概率$1-\delta$,以下不等式对所有$h\in H$都成立:
$$\mathcal{R}(h)\leq\widehat{\mathcal{R}}(h)+\sqrt{\frac{2d\log\frac{em}{d}}{m}}+\sqrt{\frac{\log\frac{1}{\delta}}{2m}}$$
我们可以将上式简写成
$$R(h)\leq\widehat{R}(h)+O(\sqrt{\frac{log(m/d)}{m/d}})$$
也就是说上界由$m/d$决定,m越大上界越小,d越大H越复杂,上界也越大。