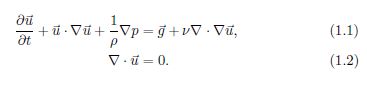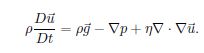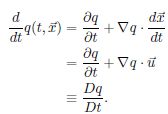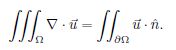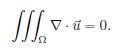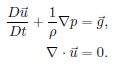【流体模拟】第一章 流体方程
坐标假设:y向上,x-z水平面。
不可压缩流体的斯托克斯方程:
速度场u,时间t,密度(density)ρ,压力p(the force per unit area that the fluid
exerts on anything.),g重力加速度,v动力学粘滞系数(kinematic viscosity)(it measures how much the fluid resists deforming while it flows (or more intuitively, how difficult it is to stir))。
方程1.1可以拆成各个基向量的分量方程。
动量方程
这个方程说到底就是牛顿第二定律。他告诉我们流体如何在力的作用下运动。
我们先将一团流体考虑成一个粒子,考虑每个例子上的作用力,首先是重力mg,然后是净压力- ∇p,然后是粘滞力,一个粘滞流体会抵抗变形,这个力将会使粒子具有相邻粒子的平均速度,也就是最小化粒子之间速度的差异。所以我们使用拉普拉斯微分算子∇ · ∇(*),这个算子度量一个量距离平均有多远(考虑图像处理中边缘检测的应用),如果我们对这一团粒子积分就能得到粘滞力,我们将使用η来表示粘滞系数,所以有η∇ ·∇u。
现在我们引出一个新的概念叫做material导数,并以此求出加速度(具体的以后会提及):
于是根据牛顿第二定律我们有:
我们将这团流体体积取极限,V变成了无穷小,我们先把他约掉得到:
现在这个粒子假设已经不存在了,然后两边同时除以密度得:
定义动力学粘滞系数为v = η/ρ有:
material导数
为了理解material导数我们先要理解两种观点——拉格朗日观点和欧拉观点。
拉格朗日观点将流体看成移动的粒子来处理,而欧拉观点则关注空间中的固定点。数值上,拉格朗日观点对应粒子,欧拉观点则对应固定的网格。
Material导数可以连接这两种观点。
在拉格朗日观点下描述t时刻在位置x的一个粒子的某一个量q时,有q(t,x)函数,作全微分可以求出此q的变化率:
这就是material导数。
在<<Fluid Simulation Computer Graphics>>中P9例子中的temperature profile T(x)=10x描述了在静止坐标系的T,而x则可能是t的函数。这样一来,两种观点就可以结合了。
最后我们将式子展开就有:
这就是动量公式。
∇ · ∇=0被称为拉普拉斯方程,而∇ · ∇=0则被称为泊松方程。
不可压缩性
取任意一戳流体体积V,DV是其边界表面,通过下列式子来度量体积变化快慢(对表面法向速度积分)
对于不可压缩流体,体积是常数,所以:
可以使用散度定理将其变换为体积分:
所以有下式:
然而这个方程应该对于任何的V(任何区域的流体)都成立,所以对于连续函数有下式:
∇ · u = 0
这就是不可压缩纳威斯托克斯方程的不可压缩条件。满足这个条件的向量场就叫做divergence-free的。
保持这个条件是模拟不可压缩流体棘手的地方之一。同是这也是压力的由来。
考虑压力的一个方法就是保持流体速度的divergence-free。
压力只出现在动量方程之中,所以我们需要想个方法把他和速度的散度联系起来。
我们在动量方程两边取散度:
第一项∇放到u前面跟不不可压缩条件有:
丢弃粘滞力
在一些情况下粘滞力很重要,比如蜂蜜或者小规模流体流。但是大多数情况下,他还是次要角色,所以我们丢了他。但事实上,多数数值方法的流体模拟都不可避免的会导致可以被解释为粘滞力的错误,所以即使我们丢了粘滞力,我们在模拟中依然会有一些类似的效果。实际上,尽可能的消除粘滞错误是CFD的一个巨大挑战。我们在以后会谈及搞粘性流体和多粘性流体,但是除此之外,我们都将假设已经丢弃了粘滞力。
没有粘滞力项的流体方程叫做欧拉方程,也叫做非粘滞流体(inviscid)。下面是不可压缩的欧拉方程:
这将是我们用的最多的方程。
边界条件
本文只会涉及两种边界条件——实体边界墙和自由表面。并且不会涉及到两种不同的流体交界,如果你感兴趣请参考[Hong and Kim 05]。
实体边界墙
速度:
前者流体不会流入或者流出它,所以:
![]()
如果边界还在移动,那么令相对速度等于0.
![]()
注意:其中法向是朝向边界的。这种情况有时被称为无粘性(no-stick)边界。因为流体可以在边界切向自由滑动,所以很重要的一点是:流体的切向速度和边界实体的切线速度没有任何联系。
压力:
自由表面:
P=0
注意:
小规模水体的表面张力,空气与流体交界,交界处压力跳跃,流体解体。这些不仔细说明了。参考相关文献。