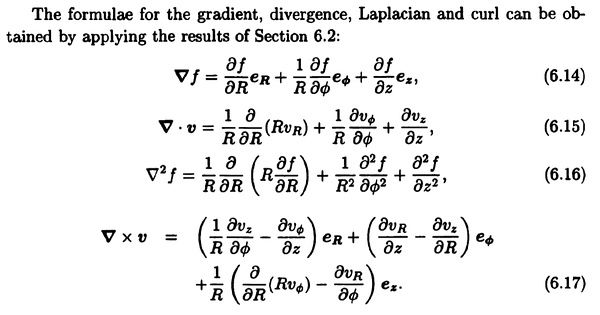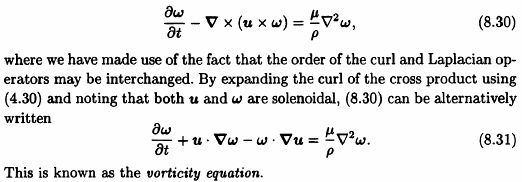<>笔记
http://book.douban.com/annotation/36251494/
<<Vector Calculus>>
by Paul C, Matthews
P4
Since the quantity of |b|*cosθ represents the component of the vector b in thedirection of the vector a, the scalar a * b can be thought of as the magnitudeof a multiplied by the component of b in the direction of a
P7
the general form of the equation of a plane is: r * a = constant.
P11
| e1 e2 e3 |
a x b=| a1 a2 a3 |
| b1 b2 b3 |
v = Ω x r
P24
The equation of a line is: r = a + λu
The second equation of a line is: r x u = b = a x u
----------------------------------------------------
1.4 Scalar triple product ([a, b, c])
The dot and the cross can be interchanged:[a, b, c]≡a * b x c = a x b * c
The vectors a, b and c can be permuted cyclically:a * b x c = b * c x a = c * a x b
The scalar triple product can be written in the form of a determinant:
| a1 a2 a3 |
a * b x c=| b1 b2 b3 |
| c1 c2 c3 |
If any two of the vectors are equal, the scalar triple product is zero.
--------------------------------------------------------
1.5 Vector triple product a x (b x c)
a x (b x c) = (a * c)*b - (a * b)*c
(a x b) x c = -(b * c)*a + (c * a)*b
--------------------------------------------------------
1.6 Scalar fields and vector fields
A scalar or vector quantity is said be a field if it is a function of position.
--------------------------------------------------------
2.2.3 Conservative vector fields
A vector field F is said to be conservative if it has the property that the line integral of F around any closed curve C is zero:
An equivalent definition is that F is conservative if the line integral of Falong a curve only depends on the endpoints of the curve, not on the pathtaken by the curve
--------------------------------------------------------
2.3.2
3.1.2 Taylor series in more than one variable
3.2 Gradient of a scalar field
The symbol ∇ can be interpreted as a vector differential operator,where the term operator means that ∇ only has a meaning when it acts on some other quantity.
Theorem 3.1
Suppose that a vector field F is related to a scalar field Φ by F = ∇Φ and ∇ exists everywhere in some region D. Then F is conservative within D.Conversely, if F is conservative, then F can be written as the gradient of a scalar field, F = ∇Φ.
If a vector field F is conservative, the corresponding scalar field Φ which obeys F = ∇Φ is called the potential(势能) for F.
--------------------------------------------------
3.3.2 Laplacian of a scalar field
4.3 The alternating tensor εijk
5.1.1 Conservation of mass for a fluid
6.1 Orthogonal curvilinear coordinates
P100
Suppose a transformation is carried out from a Cartesian coordinate system (x1, x2, x3) to another coordinate system (u1, u2, u3)
e1 =(∂x/∂u1) / h1, h1 = | ∂x/∂u1 |
e2 =(∂x/∂u2) / h2, h2 = | ∂x/∂u2 |
e3 =(∂x/∂u3) / h3, h3 = | ∂x/∂u3 |
dS = h1 * h2 * du1 * du2
dV = h1 * h2 * h3 * du1 * du2 * du3
------------------------------------------------------------------
相关内容在《微积分学教程(第三卷)》(by 菲赫金哥尔茨)里使用Jacobi式阐述的:
16章
$4. 二重积分中的变量变换
603.平面区域的变换
604.例1)(极坐标的例子)
605.曲线坐标中面积的表示法
607.几何推演
609.二重积分中的变量变换
17章 曲面面积,曲面积分
619. 例2 (引入A,B,C)
626 曲面面积的存在及其计算
629 例14)球面极坐标的计算
18章 三重积分及多重积分
$3 三重积分中的变量变换
655. 空间的变换及曲线坐标
656 例1 圆柱坐标,例2球坐标
657 曲线坐标下的体积表示法 (得出曲面坐标下的体积元素)
659 几何推演
661 三重积分中的变量变换
------------------------------------------------------------------
Summary of Chapter 6
The system (u1, u2, u3) is orthogonal if ei * ej = δij.
------------------------------------
7. Cartesian Tensors
7.1 Coordinate transformations
A matrix with this property, that its inverse is equal to its transpose, is said to be orthogonal。
So far we have only considered a two-dimensional rotation of coordinates. Consider now a general three-dimensional rotation. For a position vector x = x1e1 + x2e2 + x3e3,
x' = e'i * x (x在e'i上的投影) = e'i * (e1*x1 + e2*x2 + e3*x3) = e'i * ei*xi
xi = Lji * x'j ..........................(7.6)
7.2 Vectors and scalars
A quantity is a tensor if each of the free suffices transforms according to the rule (7.4).Lij * Lkj = δik
7.3.3 Isotropic tensors
The two tensors δij and εijk have a special property. Their components are the same in all coordinate systems. A tensor with this property is said to be isotropic.
7.4 Physical examples of tensors
7.4.1 Ohm's law
This is why δik is said to be an isotropic tensor: it represents the relationship between two vectors that are always parallel, regardless of their direction.
----------------------------------------------
8 Applications of Vector Calculus
----------------------------------------------
----------------------------------------------
8.5 Fluid mechanics
----------------------------------------------
----------------------------------------------
----------------------------------------------
----------------------------------------------
Example 8.12
Choosing the x-axis to be parallel to the channel walls, the velocity u hasthe form u = (u, 0, 0). As the fluid is incompressible(所有点的速度(沿x轴)相同), ∇u = 0, so ∂u/∂x = 0.