R:克里金插值及交叉验证浅析 Kriging interpolation and cross validation

克里金插值的基本介绍可以参考ARCGIS的帮助文档[1]. 其本质就是根据已知点的数值，确定其周围点（预测点）的数值。最直观的方法就是找到已知点和预测点数值之间的关系，从而预测出预测点的数值。比如IDW插值方法，就是假设已知点和预测点的值跟它们相对距离成反比。克里金插值的精妙之处在于它不仅考虑了已知点和预测点的距离关系，还考虑了这些已知点之间的自相关关系。

如何衡量已知点之间的自相关关系呢？通常使用的就是半变异函数，其公式如下[1]：

Semivariogram(distance h) = 0.5 * average((value i – value j)2)

这就是克里金插值不同于其他插值方法的核心所在，通过计算每个距离范围内所有配对点的离差平方和，就可以绘制出不同距离范围下的变差值图，如下示意图[1]。我们知道，离差平方和是衡量一组数据变化程度的量，而这里通过计算所有已知点与其不同距离范围内邻居点集的距离离差平方和，就可以大致衡量出已知点与不同距离范围邻居点的变化程度关系，通常的做法是进行曲线拟合，常用的包括指数拟合、球面拟合、高斯拟合等。而这个拟合的结果就是我们插值所需要的块金值、基台值等。

 

注意，目前为止这里只涉及到克里金插值是如何分析已知点信息，以及如何构造这些已知点之间的关系，整个插值（预测）过程就是假设这种已知点之间的关系：距离关系和自相关关系，对于预测点同样适用！

 

然而，在没有更多信息的前提下，我们如何知道这种插值是否可信？目前较为合理的方法就是交叉验证Cross validation。其本质是拿出一些已知点作为预测点，这些被拿出的点不参与上述已知点关系的探索过程，而是作为验证数据来衡量我们预测是否合理。比如，我们每次拿出一个已知点作为验证数据，来验证这个点的预测值，我们就可以得到所有已知点与其预测值之间的偏差，这个所有点的偏差从某种程度上讲就为我们提供了整个预测方法是否合理的依据。

一个基于R gstat空间插值包的示例：

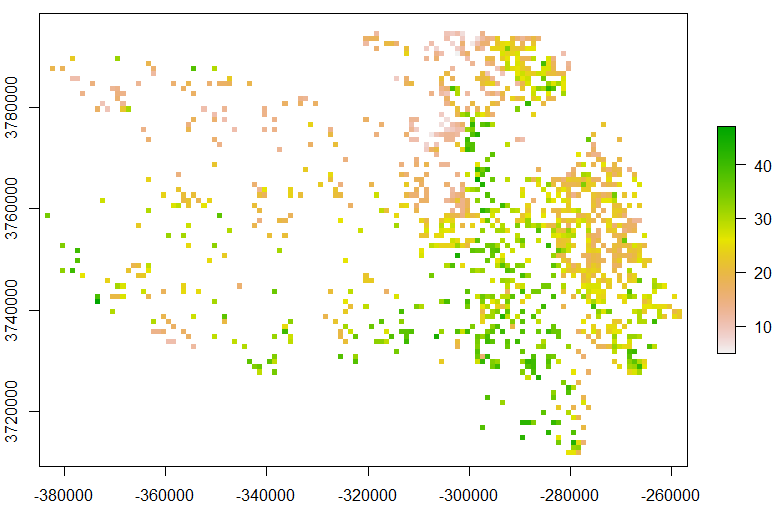
如下图，假设我们已知的数据点的栅格图，需要插值出其它预测点的值（白色透明区域）：

首先，我们需要将这个栅格数据读入到R中(需要安装raster包)

install.packages("raster")

library(raster)

data.observed <- raster("C:/Users/workspace/allmax.img")

因为gstat都是以data  frame的格式进行数据处理，首先我们编写一个函数，将这个栅格数据转化为data frame：

raster_to_dataframe<- function(inRaster, name) # 
{
  rp<- rasterToPoints(inRaster)
  df = data.frame(rp)
  colnames(df) = c("X", "Y", "VALUE")
  df$NAME<- name
  return(df)
}

name参数可以是随意的字符串，方便与其他data frame合并的时候辨别数据，这时候我们调用此函数，如下：
data.observed <- raster_to_dataframe (data.observed, "Observed") 
查看转换为data frame的结果，可以使用：
head(data.observed)

          X       Y VALUE    NAME
1 -318466.5 3794841    12 Observed
2 -304466.5 3794841    10 Observed
3 -303466.5 3794841     9 Observed
4 -302466.5 3794841    11 Observed
5 -301466.5 3794841     7 Observed
6 -297466.5 3794841    14 Observed

好了，接下来就是要分析这写已知点，gstat提供了半变异图绘制函数variogram:

v<- variogram(object = VALUE~1,data = df.wg,locations =~X+Y, width= 200)
plot(v)

通过观察，已知点的自相关关系semivariance随着距离distance的增加，呈现出指数形式的减弱（还记得吗？离差平方和？值越小，代表关系越强），所以通过观察半变异方差的分布，确定使用指数模型来拟合：

v.fit = fit.variogram(v, vgm(model = "Exp", psill= 45, range = 20000, kappa = 10),fit.sills = 50)
plot(v, model=v.fit)
v.fit

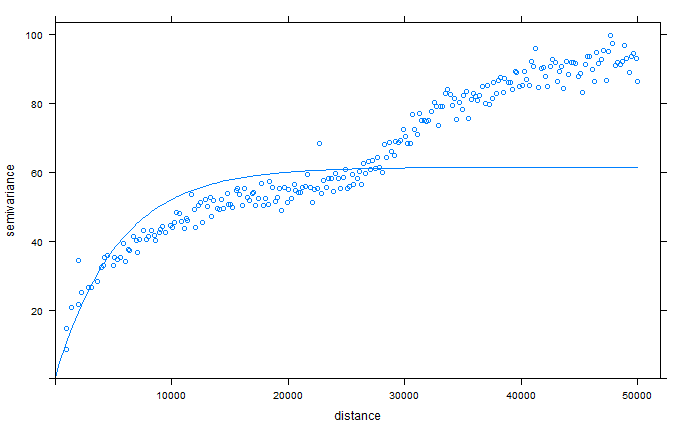
如何确定pstill, range等初始值呢，同样通过观察大致给出即可，fit.variogram()函数会自动计算出正确的结果，这个初始值存在的作用只是辅助计算，不用十分正确，其结果如下图：

　　

 

 

model psill range
1 Exp 61.39472 5326.663

可以看出，R计算出了新的psill和range值。

接下来，我们就可以利用上述分析的信息，进行克里金插值。这里使用的是krige函数：

kingnewdata<- raster_to_dataframe2(max.allgf, "Interpolate location")
aa<- krige(formula = VALUE~1,locations =~X+Y , model = vgm(61.39472, "Exp", 5326.663 , 10) , data = data.observed, newdata= kingnewdata, nmax=12, nmin=10)

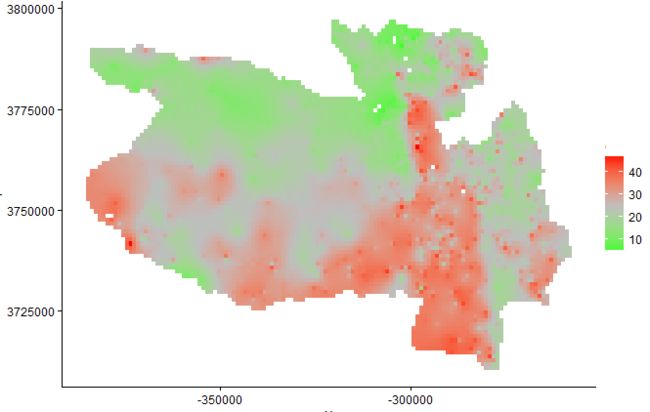
参数formula指出已知点和其他信息的关系（假如本例已知点代表土壤含水量，我们也知道这些点对应的降雨信息，那么这里的公式就是土壤含水量和降雨的简单线性关系），这里我们没有其他信息，就是普通克里金插值。参数location是已知点的坐标，这里X代表经度，Y值代表纬度。参数model就是我们上边分析的指数模型，使用拟合后的参数即可。data表示要使用的已知点的数据框。newdata表示要插值的点的位置，注意要包含和data参数所使用的dataframe一样的变量名称（本例中位置是大写X， Y），nmax和nmin是最多和最少搜索的点数，其他参数大家可以参考帮助文档，插值的结果如下：

 

好了，我们已经完成了克里金插值所有任务并且得到了我们所需要插值图，但是怎么才能知道我们的插值结果可信与否呢？当然，如果我们有预测点的实际数据，我们可以评价插值结果的精度，但是很多情况下，我们没有这些数据，cross validaion应运而生。对于克里金插值，gstat提供的cross validation函数是krige.cv()，对于本文，只需要如下代码即可完成cross validation：

kriging<- krige.cv(formula = VALUE~1, locations = ~X+Y, model = vgm(61.39472, "Exp", 5326.663 , 10), data = data.observed ,nfold= nrow(data.observed))
head(kriging)

注意，krige.cv()函数本质上是进行很多次克里金插值，然后我们就可以分析被拿出的已知点的值和预测值，估计克里金插值的可信性。这里我们每次拿出一个点，所以nfold的值设置为和data.observed的行数一样，可以看到结果：

  var1.pred var1.var observed  residual     zscore fold         X       Y
1 19.020820 31.29921       12 -7.020820 -1.2549348    1 -318466.5 3794841
2 11.220626 27.62193       10 -1.220626 -0.2322499    2 -304466.5 3794841
3 10.758057 24.82611        9 -1.758057 -0.3528407    3 -303466.5 3794841
4  9.200462 24.85426       11  1.799538  0.3609613    4 -302466.5 3794841
5 10.840395 27.07824        7 -3.840395 -0.7380158    5 -301466.5 3794841
6 12.446044 29.40208       14  1.553956  0.2865826    6 -297466.5 3794841

结果包含了预测值，预测值的方差，已知值，残差，z统计量值等，我们可以绘制出z统计量图： 

ggplot(data = kriging, aes(x=X,y=Y))+
  geom_raster( aes(fill= zscore)) +
  scale_fill_gradient2( name="zscore",low = "green",
                        mid = "grey", high = "red", midpoint = 0,
                        space = "rgb", na.value = "grey50")  

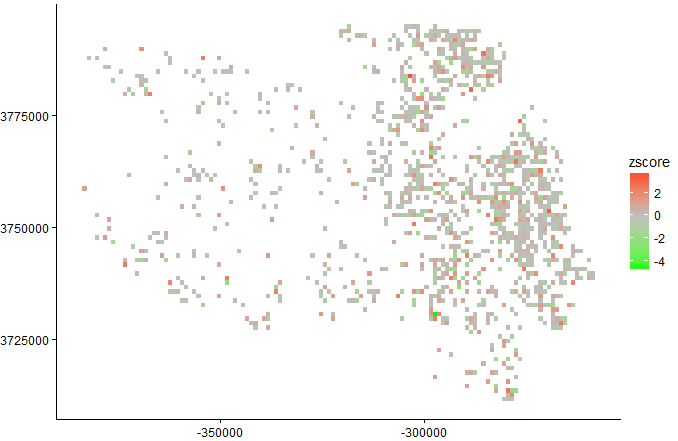
结果如下：

 或者其直方图来评价插值方案：

par(mar=c(2,2,2,2))
hist(kriging$zscore)

　　

 

欢迎大家留言讨论，转载请注明出处 http://www.cnblogs.com/ABMRG/p/5186727.html 。

 

参考文献：

[1] http://desktop.arcgis.com/en/arcmap/10.3/tools/3d-analyst-toolbox/how-kriging-works.htm

 

 

 

 

关于R基本栅格数据处理我推荐一篇博文：http://rstudio-pubs-static.s3.amazonaws.com/1057_1f7e9ac569644689b7e4de78c1fece90.html