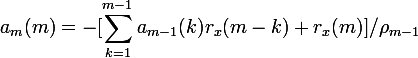现代数字信号处理——AR模型
本文目标:分析AR模型并求解AR模型的输出x(n)的功率谱。
1. AR模型概念观
数字信号处理功率谱估计方法分经典功率谱估计和现代功率谱估计,现代功率谱估计以参数模型功率谱估计为代表,参数功率谱模型如下:
u(n) ——> H(z) ——> x(n)
参数模型的基本思路是:
—— 参数模型假设研究过程是由一个输入序列u(n)激励一个线性系统H(z)的输出。
—— 由假设参数模型的输出x(n)或其自相关函数![]() 来估计H(z)的参数
来估计H(z)的参数
—— 由H(z)的参数估计x(n)的功率谱
因此,参数模型功率谱的求解有两步:
(1)H(z)模型参数估计
(2)依据模型参数求功率谱
AR模型(自回归模型,Auto Regression Model)是典型的现代参数功模型。其定义为
其中,输入设定为方差为![]() 的白噪声序列,ak是模型的参数,p是模型的阶数,Px为x(n)功率谱,也即本文要求解的目标。
的白噪声序列,ak是模型的参数,p是模型的阶数,Px为x(n)功率谱,也即本文要求解的目标。
AR模型是一个全极点模型,“自回归”的含义是:现在的输出是现在的输入和过去p个输出的加权和。
现在我们希望建立AR参数模型和x(n)的自相关函数的关系,也即AR模型的正则方程:
上面的正则方程也称Yule-Walker方程,其中的rx为自相关函数。由方程可以看出,一个p阶的AR模型有p+1个参数(![]() )。
)。
通过推导可以发现,AR模型与线性预测器是等价的,AR模型是在最小平方意义上对数据的拟合。
2. AR模型参数求解——Levinson-Durbin Algorithm
定义![]() 为p阶AR模型在m阶次时的第k个系数,k=1,2,...,m。定义
为p阶AR模型在m阶次时的第k个系数,k=1,2,...,m。定义![]() 为m阶系统时的
为m阶系统时的![]() ,这也是线性预测器中前向预测的最小误差功率。此时, 一阶AR模型时有
,这也是线性预测器中前向预测的最小误差功率。此时, 一阶AR模型时有
![]()
我们定义初始时![]() ,则
,则
![]()
由PART1中矩阵的对称性质,将上面的公式推广到高阶AR模型,可以推导出Levinson-Durbin递推算法:
![]()
![]()
Levinson-Durbin递推算法从低阶开始递推,,给出了每一阶次时所有参数,。这一特点有利于我们选择合适的AR模型阶次。
因为![]() 必须大于0,由式
必须大于0,由式![]() 知
知![]() ,如果
,如果![]() ,递推应该停止。
,递推应该停止。
到此,选择最佳阶次的参数代入到![]() 中,求得功率谱。
中,求得功率谱。
3. matlab实现
matlab工具箱中提供了现成的函数实现AR模型功率谱计算。参考 [1],我们将内容摘录如下:
AR模型的谱估计是现代谱估计的主要内容。
1.AR模型的Yule—Walker方程和Levinson-Durbin递推算法:在MATLAB中,函数levinson和aryule都采用Levinson-Durbin递推算法来求解AR模型的参数a1,a2,……,ap及白噪声序列的方差,只是两者的输入参数不同,它们的格式为:
A=LEVINSON(R,ORDER) A=ARYULE(x,ORDER)
两函数均为定阶ORDER的求解,但是函数levinson的输入参数要求是序列的自相关函数,而函数aryule的输入参数为采样序列。
下面语句说明函数levinson和函数aryule的功能是相同的:
例子:
randn('seed',0)
a=[1 0.1 0.2 0.3 0.4 0.5];
x=impz(1,a,20)+randn(20,1)/20;
r=xcorr(x,'biased');
r(1:length(x)-1)=[];
A=levinson(r,5)
B=aryule(x,5)
2.Burg算法:
格式为:A=ARBURG(x,ORDER); 其中x为有限长序列,参数ORDER用于指定AR模型的阶数。以上面的例子为例:
randn('seed',0)
a=[1 0.1 0.2 0.3 0.4 0.5];
x=impz(1,a,20)+randn(20,1)/20;
A=arburg(x,5)
3.改进的协方差法:
格式为:A=ARMCOV(x,ORDER); 该函数用来计算有限长序列x(n)的ORDER阶AR模型的参数。例如:输入下面语句:
randn('seed',0)
a=[1 0.1 0.2 0.3 0.4 0.5];
x=impz(1,a,20)+randn(20,1)/20;
A=armcov(x,5)
AR模型阶数P的选择:
AR模型阶数P一般事先是不知道的,需要事先选定一个较大的值,在递推的过程中确定。在使用Levinson—Durbin递推方法时,可以给出由低阶到高阶的每一组参数,且模型的最小预测误差功率Pmin(相当于白噪声序列的方差)是递减的。直观上讲,当预测误差功率P达到指定的希望值时,或是不再发生变化时,这时的阶数即是应选的正确阶数。
因为预测误差功率P是单调下降的,因此,该值降到多少才合适,往往不好选择。比较常见的准则是:
最终预测误差准则:FPE(r)=Pr{[N+(r+1)]/ [N-(r+1)]}
信息论准则:AIC(r)=N*log(Pr)+2*r
上面的N为有限长序列x(n)的长度,当阶数r由1增加时,FPE(r) 和AIC(r)都将在某一r处取得极小值。将此时的r定为最合适的阶数p。
MATLAB中AR模型的谱估计的函数说明:
1. Pyulear函数:
功能:利用Yule--Walker方法进行功率谱估计.
格式: Pxx=Pyulear(x,ORDER,NFFT)
[Pxx,W]=Pyulear(x,ORDER,NFFT)
[Pxx,W]=Pyulear(x,ORDER,NFFT,Fs)
Pyulear(x,ORDER,NFFT,Fs,RANGE,MAGUNITS)
说明:Pxx =Pyulear(x,ORDER,NFFT)中,采用Yule--Walker方法估计序列x的功率谱,参数ORDER用来指定AR模型的阶数,NFFT为FFT算法的长度,默认值为256,若NFFT为偶数,则Pxx为(NFFT/2 + 1)维的列矢量,若NFFT为奇数,则Pxx为(NFFT + 1)/2维的列矢量;当x为复数时,Pxx长度为NFFT。
[Pxx,W]=Pyulear(x,ORDER,NFFT)中,返回一个频率向量W.
[Pxx,W]=Pyulear(x,ORDER,NFFT,Fs)中,可以在F向量得到功率谱估计的频率点,Fs指定采样频率。
Pyulear(x,ORDER,NFFT,Fs,RANGE,MAGUNITS)中,直接画出功率谱估计的曲线图。
2. Pburg函数:
功能:利用Burg方法进行功率谱估计。
格式:Pxx=Pburg(x,ORDER,NFFT)
[Pxx,W]=Pburg(x,ORDER,NFFT)
[Pxx,W]=Pburg(x,ORDER,NFFT,Fs)
Pburg(x,ORDER,NFFT,Fs,RANGE,MAGUNITS)
说明:Pburg函数与Pyulear函数格式相同,只是计算AR模型时所采用的方法不同,因此格式可以参照Pyulear函数。
3. Pcov函数:
功能:利用协方差方法进行功率谱估计。
格式:Pxx=Pcov(x,ORDER,NFFT)
[Pxx,W]=Pcov(x,ORDER,NFFT)
[Pxx,W]=Pcov(x,ORDER,NFFT,Fs)
Pcov(x,ORDER,NFFT,Fs,RANGE,MAGUNITS)
说明:Pcov函数采用协方差法估计AR模型的参数,然后计算序列x的功率谱。协方差法与改进的协方差法相比,前者仅令前向预测误差为最小,其他步骤是一样的。:Pcov函数与Pyulear函数格式相同,只是计算AR模型时所采用的方法不同,因此格式可以参照Pyulear函数.
4.Pmcov:
功能:利用改进的协方差方法进行功率谱估计。
格式:Pxx=Pmcov(x,ORDER,NFFT)
[Pxx,W]=Pmcov(x,ORDER,NFFT)
[Pxx,W]=Pmcov(x,ORDER,NFFT,Fs)
Pmcov(x,ORDER,NFFT,Fs,RANGE,MAGUNITS)
例如:输入下面语句:
figure 8.10--8.11
Fs=1000; %采样频率
n=0:1/Fs:3;
xn=cos(2*pi*n*200)+randn(size(n));
%设置参数
order=20;
nfft=1024;
%Yule-Walker方法
figure(1)
pyulear(xn,order,nfft,Fs);
%Burg方法
figure(2)
pburg(xn,order,nfft,Fs);
%协方差法
figure(3)
pcov(xn,order,nfft,Fs);
%改进协方差方法
figure(4)
pmcov(xn,order,nfft,Fs);
AR谱的分辨率:
经典谱估计的分辨率反比与信号的有效长度,但是现代谱估计的分辨率可以不受此限制. 这是因为对于给定的N点有限长序列x(n),虽然其估计出的相关函数也是有限长的,但是现代谱估计的一些方法隐含着数据和自相关函数的外推,使其可能的长度超过给定的长度,因而AR谱的分辨率较高。
例如:序列x(n)由两个正铉信号组成,其频率分别为f1=20Hz和f2=21Hz,并含有一定的噪声量。试分别用周期图法,Burg方法与改进的协方差法估计信号的功率谱,且AR模型的阶数取30和50两种情况讨论。
上面的例子可以通过下面程序实现:
Fs=200;
n=0:1/Fs:1;
xn=sin(2*pi*20*n)+sin(2*pi*21*n)+0.1*randn(size(n));
window=boxcar(length(xn));
nfft=512;
[Pxx,f]=periodogram(xn,window,nfft,Fs);
figure(1)
plot(f,10*log10(Pxx)),grid
xlabel('Frequency(Hz)')
ylabel('Power Spectral Density(dB/Hz)')
title('Periodogram PSD Estimate')
order1=30;
order2=50;
figure(2)
pburg(xn,order1,nfft,Fs)
figure(3)
pburg(xn,order2,nfft,Fs)
figure(4)
pmcov(xn,order1,nfft,Fs)
figure(5)
pmcov(xn,order1,nfft)
4. C语言实现
/*
* ar_model.h
*
* Created on: 2013-8-11
* Author: monkeyzx
*/
#ifndef AR_MODEL_H_
#define AR_MODEL_H_
typedef struct {
float real;
float imag;
} complex;
extern void maryuwa(complex x[],complex a[],complex r[],int n,int ip,
float *ep,int *ierror);
extern void mpsplot(float psdr[],float psdi[],int mfre,float ts);
extern void zx_ar_model(void);
#endif /* AR_MODEL_H_ */
/*
* ar_model.c
*
* Created on: 2013-8-11
* Author: monkeyzx
*/
#include <stdio.h>
#include <stdlib.h>
#include <math.h>
#include <stdlib.h>
//#include "msp.h"
#include "ar_model.h"
#include "time.h"
float mabs(complex a)
{
float m;
m=a.real*a.real+a.imag*a.imag;
m=sqrt(m);
return(m);
}
/*---------------------------------------------------------------------
Routine MCORRE1:To estimate the biased cross-correlation function
of complex arrays x and y. If y=x,then it is auto-correlation.
input parameters:
x :n dimensioned complex array.
y :n dimensioned complex array.
n :the dimension of x and y.
lag:point numbers of correlation.
output parameters:
r :lag dimensioned complex array, the correlation function is
stored in r(0) to r(lag-1).
in Chapter 1 and 11
---------------------------------------------------------------------*/
void mcorre1(complex x[],complex y[],complex r[],int n,int lag)
{
int m,j,k;
for(k=0;k<lag;k++) {
m=n-1-k;
r[k].real=0.0f;
r[k].imag=0.0f;
for(j=0;j<=m;j++) {
r[k].real+=y[j+k].real*x[j].real+y[j+k].imag*x[j].imag;
r[k].imag+=y[j+k].imag*x[j].real-y[j+k].real*x[j].imag;
}
r[k].real=r[k].real/n;
r[k].imag=r[k].imag/n;
}
return;
}
/*---------------------------------------------------------------------
Routine maryuwa: To determine the autoregressive coefficients by
solving Yule-Walker equation with Levinson algorithm.
Input Parameters:
n : Number of data samples (integer)
ip : Order of autoregressive model
x : Array of complex data values, x(0) to x(n-1)
Output Parameters:
ep : Driving noise variance (real)
a : Array of complex autoregressive coefficients, a(0) to
a(ip)
ierror=0 : No error
=1 : ep<=0 .
r : complex work array, auto-correlation
in chapter 12
--------------------------------------------------------------------*/
void maryuwa(complex x[],complex a[],complex r[],int n,int ip,
float *ep,int *ierror)
{
complex sum;
int i,k;
float r0;
*ierror=1;
mcorre1(x,x,r,n,ip+1);
a[0].real=1.0;
a[0].imag=0.0;
r0=r[0].real;
a[1].real=-r[1].real/r0;
a[1].imag=-r[1].imag/r0;
*ep=r0*(1.0f-pow(mabs(a[1]),2));
for(k=2;k<=ip;k++) {
sum.real=0.;
sum.imag=0.;
for(i=1;i<k;i++) {
sum.real+=r[k-i].real*a[i].real-r[k-i].imag*a[i].imag;
sum.imag+=r[k-i].real*a[i].imag+r[k-i].imag*a[i].real;
}
sum.real+=r[k].real;
sum.imag+=r[k].imag;
a[k].real=-sum.real/(*ep);
a[k].imag=-sum.imag/(*ep);
(*ep)*=1.-pow(mabs(a[k]),2);
if(*ep<=0.0)
return;
for(i=1;i<k;i++) {
x[i].real=a[i].real+a[k-i].real*a[k].real+
a[k-i].imag*a[k].imag;
x[i].imag=a[i].imag+a[k-i].real*a[k].imag-
a[k-i].imag*a[k].real;
}
for(i=1;i<k;i++) {
a[i].real=x[i].real;
a[i].imag=x[i].imag;
}
}
*ierror=0;
}
/*----------------------------------------------------------------------
routinue mrelfft:To perform split-radix DIF fft algorithm.
input parameters:
xr,xi:real and image part of complex data for DFT/IDFT,n=0,...,N-1
N :Data point number of DFT compute .
isign:Transform direction disignator ,
isign=-1: For Forward Transform.
isign=+1: For Inverse Transform.
output parameters:
xr,xi:real and image part of complex result of DFT/IDFT,n=0,...,N-1
Note: N must be a power of 2 .
in chapter 5
---------------------------------------------------------------------*/
void mrelfft(float xr[],float xi[],int n,int isign)
{
float e,es,cc1,ss1,cc3,ss3,r1,s1,r2,s2,s3,xtr,xti,a,a3;
int m,n2,n4,j,k,is,id,i0,i1,i2,i3,n1,i,nn;
for(m=1;m<=16;m++) {
nn=pow(2,m);
if(n==nn)break;
}
if(m>16) {
#ifdef _DEBUG
printf(" N is not a power of 2 ! \n");
#endif
return;
}
n2=n*2;
es=-isign*atan(1.0)*8.0;
for(k=1;k<m;k++) {
n2=n2/2;
n4=n2/4;
e=es/n2;
a=0.0;
for(j=0;j<n4;j++) {
a3=3*a;
cc1=cos(a);
ss1=sin(a);
cc3=cos(a3);
ss3=sin(a3);
a=(j+1)*e;
is=j;
id=2*n2;
do {
for(i0=is;i0<n;i0+=id) {
i1=i0+n4;
i2=i1+n4;
i3=i2+n4;
r1=xr[i0]-xr[i2];
s1=xi[i0]-xi[i2];
r2=xr[i1]-xr[i3];
s2=xi[i1]-xi[i3];
xr[i0]+=xr[i2];
xi[i0]+=xi[i2];
xr[i1]+=xr[i3];
xi[i1]+=xi[i3];
if(isign!=1) {
s3=r1-s2;
r1=r1+s2;
s2=r2-s1;
r2=r2+s1;
} else {
s3=r1+s2;
r1=r1-s2;
s2=-r2-s1;
r2=-r2+s1;
}
xr[i2]=r1*cc1-s2*ss1;
xi[i2]=-s2*cc1-r1*ss1;
xr[i3]=s3*cc3+r2*ss3;
xi[i3]=r2*cc3-s3*ss3;
}
is=2*id-n2+j;
id=4*id;
}while(is<n-1);
}
}
/* ------------ special last stage -------------------------*/
is=0;
id=4;
do {
for(i0=is;i0<n;i0+=id) {
i1=i0+1;
xtr=xr[i0];
xti=xi[i0];
xr[i0]=xtr+xr[i1];
xi[i0]=xti+xi[i1];
xr[i1]=xtr-xr[i1];
xi[i1]=xti-xi[i1];
}
is=2*id-2;
id=4*id;
} while(is<n-1);
j=1;
n1=n-1;
for(i=1;i<=n1;i++) {
if(i<j) {
xtr=xr[j-1];
xti=xi[j-1];
xr[j-1]=xr[i-1];
xi[j-1]=xi[i-1];
xr[i-1]=xtr;
xi[i-1]=xti;
}
k=n/2;
while(1) {
if(k>=j)break;
j=j-k;
k=k/2;
}
j=j+k;
}
if(isign==-1) return;
for(i=0;i<n;i++) {
xr[i]/=n;
xi[i]/=n;
}
}
/*---------------------------------------------------------------------
Routine mpsplot: To plot the normalized power spectum curve on the
normalized frequency axis from -.5 to +.5 .
mfre : Points in frequency axis and must be the power of 2.
ts : Sample interval in seconds (real).
psdr : Real array of power spectral density values.
psdi : Real work array.
in chapter 11,12
--------------------------------------------------------------------*/
void mpsplot(float psdr[],float psdi[],int mfre,float ts)
{
FILE *fp;
char filename[30];
int k,m2;
float pmax,fs,faxis;
m2=mfre/2;
for(k=0;k<m2;k++){
psdi[k]=psdr[k];
psdr[k]=psdr[k+m2];
psdr[k+m2]=psdi[k];
}
pmax=psdr[0];
for(k=1;k<mfre;k++)
if(psdr[k]>pmax)
pmax=psdr[k];
for(k=0;k<mfre;k++) {
psdr[k]=psdr[k]/pmax;
if(psdr[k]<=0.0)
psdr[k]=.000001;
}
fs=1./ts;
fs=fs/(float)(mfre);
printf("Please input filename:\n");
scanf("%s",filename);
if((fp=fopen(filename,"w"))==NULL) {
printf("cannot open file\n");
exit(0);
}
for(k=0;k<mfre;k++) {
faxis=fs*(k-m2);
fprintf(fp,"%f,%f\n",faxis,10.*log10(psdr[k]));
}
fclose(fp);
return;
}
/*----------------------------------------------------------------------
Routine mar1psd: To compute the power spectum by AR-model parameters.
Input parameters:
ip : AR model order (integer)
ep : White noise variance of model input (real)
ts : Sample interval in seconds (real)
a : Complex array of AR parameters a(0) to a(ip)
Output parameters:
psdr : Real array of power spectral density values
psdi : Real work array
in chapter 12
---------------------------------------------------------------------*/
void mar1psd(complex a[],int ip,int mfre,float *ep,float ts)
{
static float psdr[4096];
static float psdi[4096];
int k;
float p;
for(k=0;k<=ip;k++) {
psdr[k]=a[k].real;
psdi[k]=a[k].imag;
}
for(k=ip+1;k<mfre;k++) {
psdr[k]=0.;
psdi[k]=0.;
}
mrelfft(psdr,psdi,mfre,-1);
for(k=0;k<mfre;k++) {
p=pow(psdr[k],2)+pow(psdi[k],2);
psdr[k]=(*ep)*ts/p;
}
mpsplot(psdr,psdi,mfre,ts);
return;
}
/*
* Below are examples for using @maryuwa and @mar1psd
*/
#define PI (3.1415926)
#define N (1024)
#define AN (10)
complex x[N];
complex r[N];
complex a[AN];
/*
* generate random number which satify guass distribution
*/
double guass_rand(void)
{
static double V1, V2, S;
static int phase = 0;
double X;
if ( phase == 0 ) {
do {
double U1 = (double)rand() / RAND_MAX;
double U2 = (double)rand() / RAND_MAX;
V1 = 2 * U1 - 1;
V2 = 2 * U2 - 1;
S = V1 * V1 + V2 * V2;
} while(S >= 1 || S == 0);
X = V1 * sqrt(-2 * log(S) / S);
} else {
X = V2 * sqrt(-2 * log(S) / S);
}
phase = 1 - phase;
return X;
}
void zx_ar_model(void)
{
int i=0;
float ep = 0;
int ierror = 0;
/*
* generate x[N]
*/
srand(time(NULL));
for (i=0; i<N; i++) {
x[i].real = sin(2*PI*i/N) + guass_rand();
x[i].imag = 0;
}
/* Find parameters for AR model */
maryuwa(x, a, r, N, AN, &ep, &ierror);
/* Calculate power spectum using parameters of AR model */
mar1psd(a, AN, N, &ep, 1);
}
/*
* main.c
*
* Created on: 2013-8-11
* Author: monkeyzx
*/
#include "ar_model.h"
int main(void)
{
zx_ar_model();
return 0;
}
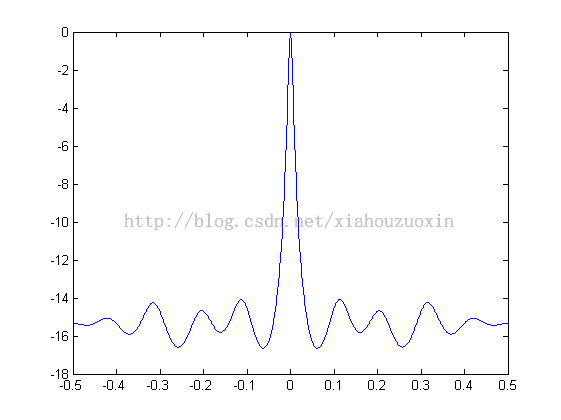
上面的实例中给定输入信号为余弦信号,采样点数为1024个点,通过计算后的功率谱通过mpsplot函数保存到文本文件output.txt中,保存格式如下:
-0.500000,-15.334630
-0.499023,-15.334833
-0.498047,-15.335444
-0.497070,-15.336456
-0.496094,-15.337864
-0.495117,-15.339655
-0.494141,-15.341816
-0.493164,-15.344331
-0.492188,-15.347179
-0.491211,-15.350342
-0.490234,-15.353794
-0.489258,-15.357505
-0.488281,-15.361453
-0.487305,-15.365603
-0.486328,-15.369924
-0.485352,-15.374381
......
最后借助matlab读取该文件,绘制出功率谱的图形
data = load('output.txt');
plot(data(:,1),data(:,2));
关于上面的C程序,这里只提与主题无关的,double guass_rand(void)是C语言中典型的生成高斯分布随机数的发生器,这里用于在余弦函数上加上一个高斯的噪声。关于更多的随机数生成器可参考关于怎样产生随机数的彻底研究 [自行理解],我将该博文转载过来,感谢作者。
Refrences:
[1] 胡广书《数字信号处理——理论、算法与实现 第二版》
[2] AR模型matlab相关函数描述http://blog.sina.com.cn/s/blog_62f573ad0100sfh1.html