Logistic Regression——用线解决问题
LR一般用于预测二分类问题,即yes no和0\1问题,我们构建了X(设备属性和行为属性),我们需要预测Y(是否异常),而反作弊项目中,我们需要预测的就是设备作弊or正常,即0\1问题。选择LR一个很重要的原因是我们相信X和Y是有联系的,不同的类型的Y会有不同的X表现。
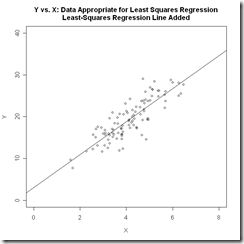
而X和Y是否有线性关系? 普通线性回归(Ordinary Linear Regression)是否就能满足需求?我们需要先论证这个问题,我们看一下普通线性回归,模型是这样的:
![]()
在线性回归中,随机误差项服从正态分布。这也意味着回归的Y值是个连续变量,不能是0\1这样的binary变量。另外一个解释就是线性回归对响应变量Y的要求是有常数方差,这也限定了Y的分布,就比如二项分布的Y就没有常数方差。这也正符合我们常规的阅读理解,回归用于定量分析,更多的在拟合和预测量上,而分类是个定性分析。正因为OLR的做法限制太多,因此有了通用线性回归的方法(General Linear Regression),通用方法的思路就是寻求一个转换函数g来作用于输入变量X,从而摆脱对Y的分布限制。具体表现为
![]()
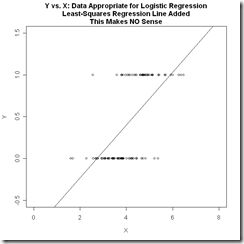
下面两张图对比了线性回归和逻辑回归数据的特点,也说明了如果用线性回归来分类binary数据是一个什么样的效果。
其实比较朴素的理解就是,我们把要分类的数据划分为0和1两类,那么数据其实是会以中间这幅图的形式分布的,必然存在一个平面(直线)把数据划分。而我们希望找到一个判别函数能完成区分,显而易见的是直线无法完成这个事情。
面对线性回归的劣势,我们理解回归的问题在于无法对公式(1)的结果做0\1划分,线性回归的方法做分类,就是要求
![]()
而逻辑回归作为GLR的一个特殊情况,定义了一函数f(),这个函数可以将Y做0\1处理,从而使线性回归变得有意义。而逻辑回归的做法就是找到了这样一个函数,这个函数也叫logit函数
![]()
其中我们把p等价于原来的 ,解释一下就是p代表Y=1的概率,标准说法p是Y=1时Y的期望。然后把这个p替换掉就得到了
![]()
目标是求解,于是
![]()
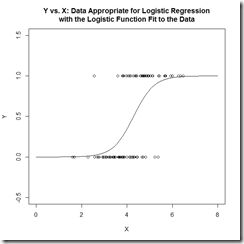
这里就不是一个线性函数了,上面提到的公式(2)对应的曲线上面最右边的图——可以看到p的函数曲线,这样的划分对于0\1数据的分类是非常合适的。
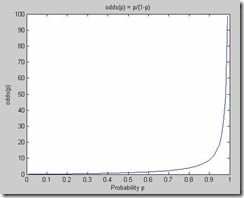
那么一个问题就随之而来,logit函数是怎么来的?要想知道答案,我们需要先分析一下这个形式,我们定义这个形式为“优势”(odds),odds有时候也叫做“几率”,odds的函数形式其实是下面左图的样子,而logit函数的形式是右图的样子
odds的理解其实要结合概率的思想,我们认为一个事件发生的概率是p,那么不发生的概率就是1-p,而odds表达的就是事件发生与不发生(或者一个标注yes 或者no)的几率,比如一个事情发生的概率是0.9,而不发生是0.1,那么odds(发生)=0.9/0.1=9,而odds(不发生)=0.1/0.9=0.1111...。这说明一种事物相比较时的优势,但是这个优势在形式上非对称,这样是不完美的,也是难于理解的,毕竟对于一个0-1之间的概率比较,结果却在0-∞之间。而可以看出logit函数是把odds对数化后得到的一个对称的美妙的曲线,拥有我们想要的所有性质,并且解决了OLR所限制的问题,而且由公式(3)我们也能看到,logit函数使结果限定在0-1之间,且是输入变量X的线性表示。
最后当我们计算出p,我们就能确定分类,比如p>0.5时 y=1,而p<0.5时y=0。于是这样的分类任务就结束了。不过我们再看看模型,似乎忘记了什么,我们可以从数据集里得到X和Y,但是对于α和β以及ε的值(参数值),我们需要获取到。而这才是LR作为机器学习方法最关键的一个部分。
我们假设数据集有n个数据样本,且n大于估计的参数的个数,于是我们令
![]()
![]()
我们用β表示整个参数向量,那么原来的表达式可以写为Y=X*β。类似最小二乘法的思路,我们有下面的推断
![]()
![]()
其实如果把目标约定为计算β,那么问题也就被归约为一个参数估计问题,而我们最常用的方法就是极大似然估计法。这里不具体介绍MLE,换种角度我们从头开始设计这个分类器。
之前考虑的点我们简化了分析,我们理所当然的认为X特征向量彼此是同等重要的,而事实往往不是这样,因此模型需要加入一个权重影响因子,也就是LR模型被扩展为Weighted Logistic Regression,因为目标是计算公式(5),加入权重后,我们把评估公式(5)的做法替换为去评估
![]()
这里就涉及一个问题:权重具体是个什么定义?权重W是个对角矩阵,其对角元素即每个特征项的权重值,而这个权重定义为预测变量的标准差。此时我们回到一个基本问题,LR用来预测二类问题,而我们一般假设我们的预测变量Y是服从二项分布的即,那么方差,更特殊的,对于单次试验是伯努利分布,所以有,而这个即我们对于预测变量Y的估计值,形如公式(4),换用现在对β的定义就是,回到公式(6)中,我们新引入的变量U即表示为,其中后面这个加项我们这么理解:分子是一个预测误差项,而分母是我们定义的权重,这样一个比值缩放了正确分类的大方差样本点和小方差样本点对结果的影响。另外需要引入的一个概念是岭回归(Ridge Regression),源于一些预测变量y可能是线性相关的,那么这会导致是奇异矩阵,会导致无穷解,因此在带求解的公式(6)的基础上,为可逆矩阵引入一个常量对角矩阵,公式变为
![]()
其中是小常量,而I是单位矩阵。这样做避免了对奇异矩阵求逆,但是带来了问题就是对预测变量结果的偏置,导致目标问题发生了小小的变化。多种方法可以帮助我们寻找一个好的,这里就不具体展开了,具体参考资料即可。
最后就是算法实现了,为了避免复杂的矩阵求逆,我们把形式变一下,将公式(7)转换为求解这样一个线性系统
![]()
其中,。可以看出,算法的输入是特征矩阵X和U(间接得到),输出是β。求解线性系统的算法有很多,其中共轭梯度算法是非常有效的算法,下面左图描述了共轭梯度算法的实现伪代码。
共轭梯度:
IRLS:
其中值得一提的是共轭梯度算法中的“is large enough”或者维基上说的“sufficiently small”有多种判断方式,具体这里就不列出了,可以看参考资料[2]。右图是迭代重加权最小二乘法,用于最终求解β。
我在github上放了一个《machine learning in action》中的LR算法的python实现,对于β的求解使用的是梯度下降法,可以参考https://github.com/changedi/mlmlml/blob/master/LogisticRegression/logRegres.py,而关于梯度下降等最优化算法,我想还是单独开一篇去介绍比较合适。至此,LR的基本介绍基本就结束了。
文中除流程图外,其他截图取自ref[2],特此声明。
References:
[1] http://logisticregressionanalysis.com/86-what-is-logistic-regression/
[2] http://www.omidrouhani.com/research/logisticregression/html/logisticregression.htm
[3] 《统计学习方法》,李航
[4] Logit Models for Binary Data, G. Rodriguez, 2007
[5] http://zh.wikipedia.org/wiki/%E5%85%B1%E8%BD%AD%E6%A2%AF%E5%BA%A6%E6%B3%95
[6] http://cnx.org/content/m45285/latest/