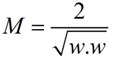SVM支持向量机算法
参考资料:http://www.cppblog.com/sunrise/archive/2012/08/06/186474.html http://blog.csdn.net/sunanger_wang/article/details/7887218
我的数据挖掘算法代码:https://github.com/linyiqun/DataMiningAlgorithm
介绍
svm(support vector machine)是一种用来进行模式识别,模式分类的机器学习算法。svm的主要思想可以概括为2点:(1)、针对线性可分情况进行分析。(2)、对于线性不可分的情况,通过使用核函数,将低维线性不可分空间转化为高维线性可分的情况,然后在进行分析。目前已经有实现好的svm的算法包,在本文的后半部分会给出我实现好的基于libsvm包的svm分类代码。
SVM算法原理
svm算法的具体原理得要分成2部分,一个是线性可分的情况,一个是线性不可分的情况,下面说说线性可分的情况:
线性可分的情况
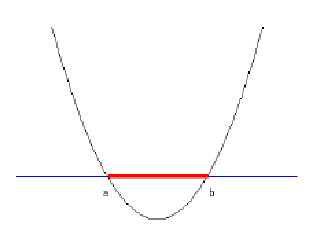
下面是一个二维空间的形式:
比如上面所示的情况,最佳的分类情况,应该是上面的margin的大小最大的时候,保证了分类的最准确。这里省去了一些数学的推理证明。要使用下面这个最大化:
反过来说,就是要使分母位置最小:
就是让||w||最小,当然这里会有个限制条件,就是这个线的应该有分类的作用,也就是说,样本数据代入公式,至少会有分类,于是限制条件就来了:
s.t的意思是subject to,也就是在后面这个限制条件。这就是问题的最终表达形式。后面这个式子会经过一系列的转换,最终变成这个样子:
这个就是我们需要最终优化的式子。至此,得到了线性可分问题的优化式子。如果此时你问我如何去解这个问题,很抱歉的告诉你,我也不知道(悔恨当初高数没学好....)
线性不可分的情况
同样给出一张图:
我们只能找出这样的条曲线将ab这个条线段进行分割。这时,就用到了在开始部分介绍的4个核函数。
限制条件为:
上面为线性可分的情况,不可分的情况可通过核函数自动转为线性可分情况。在整个过程中,省去了主要的推理过程,详细的可以点击最上方提供的2个链接。
svm的算法实现
这里提供我利用libsvm库做一个模式分类。主要的过程为:
1、输入训练集数据。
2、提供训练集数据构建svm_problem参数。
3、设定svm_param参数中的svm类型和核函数类型。
4、通过svm_problem和svm_param构建分类模型model。
5、最后通过模型和测试数据输出预测值。
SVMTool工具类代码:
package DataMining_SVM;
import java.io.BufferedReader;
import java.io.File;
import java.io.FileReader;
import java.util.ArrayList;
import java.util.List;
import DataMining_SVM.libsvm.svm;
import DataMining_SVM.libsvm.svm_model;
import DataMining_SVM.libsvm.svm_node;
import DataMining_SVM.libsvm.svm_parameter;
import DataMining_SVM.libsvm.svm_problem;
/**
* SVM支持向量机工具类
*
* @author lyq
*
*/
public class SVMTool {
// 训练集数据文件路径
private String trainDataPath;
// svm_problem对象,用于构造svm model模型
private svm_problem sProblem;
// svm参数,里面有svm支持向量机的类型和不同 的svm的核函数类型
private svm_parameter sParam;
public SVMTool(String trainDataPath) {
this.trainDataPath = trainDataPath;
// 初始化svm相关变量
sProblem = initSvmProblem();
sParam = initSvmParam();
}
/**
* 初始化操作,根据训练集数据构造分类模型
*/
private void initOperation(){
}
/**
* svm_problem对象,训练集数据的相关信息配置
*
* @return
*/
private svm_problem initSvmProblem() {
List<Double> label = new ArrayList<Double>();
List<svm_node[]> nodeSet = new ArrayList<svm_node[]>();
getData(nodeSet, label, trainDataPath);
int dataRange = nodeSet.get(0).length;
svm_node[][] datas = new svm_node[nodeSet.size()][dataRange]; // 训练集的向量表
for (int i = 0; i < datas.length; i++) {
for (int j = 0; j < dataRange; j++) {
datas[i][j] = nodeSet.get(i)[j];
}
}
double[] lables = new double[label.size()]; // a,b 对应的lable
for (int i = 0; i < lables.length; i++) {
lables[i] = label.get(i);
}
// 定义svm_problem对象
svm_problem problem = new svm_problem();
problem.l = nodeSet.size(); // 向量个数
problem.x = datas; // 训练集向量表
problem.y = lables; // 对应的lable数组
return problem;
}
/**
* 初始化svm支持向量机的参数,包括svm的类型和核函数的类型
*
* @return
*/
private svm_parameter initSvmParam() {
// 定义svm_parameter对象
svm_parameter param = new svm_parameter();
param.svm_type = svm_parameter.EPSILON_SVR;
// 设置svm的核函数类型为线型
param.kernel_type = svm_parameter.LINEAR;
// 后面的参数配置只针对训练集的数据
param.cache_size = 100;
param.eps = 0.00001;
param.C = 1.9;
return param;
}
/**
* 通过svm方式预测数据的类型
*
* @param testDataPath
*/
public void svmPredictData(String testDataPath) {
// 获取测试数据
List<Double> testlabel = new ArrayList<Double>();
List<svm_node[]> testnodeSet = new ArrayList<svm_node[]>();
getData(testnodeSet, testlabel, testDataPath);
int dataRange = testnodeSet.get(0).length;
svm_node[][] testdatas = new svm_node[testnodeSet.size()][dataRange]; // 训练集的向量表
for (int i = 0; i < testdatas.length; i++) {
for (int j = 0; j < dataRange; j++) {
testdatas[i][j] = testnodeSet.get(i)[j];
}
}
// 测试数据的真实值,在后面将会与svm的预测值做比较
double[] testlables = new double[testlabel.size()]; // a,b 对应的lable
for (int i = 0; i < testlables.length; i++) {
testlables[i] = testlabel.get(i);
}
// 如果参数没有问题,则svm.svm_check_parameter()函数返回null,否则返回error描述。
// 对svm的配置参数叫验证,因为有些参数只针对部分的支持向量机的类型
System.out.println(svm.svm_check_parameter(sProblem, sParam));
System.out.println("------------检验参数-----------");
// 训练SVM分类模型
svm_model model = svm.svm_train(sProblem, sParam);
// 预测测试数据的lable
double err = 0.0;
for (int i = 0; i < testdatas.length; i++) {
double truevalue = testlables[i];
// 测试数据真实值
System.out.print(truevalue + " ");
double predictValue = svm.svm_predict(model, testdatas[i]);
// 测试数据预测值
System.out.println(predictValue);
}
}
/**
* 从文件中获取数据
*
* @param nodeSet
* 向量节点
* @param label
* 节点值类型值
* @param filename
* 数据文件地址
*/
private void getData(List<svm_node[]> nodeSet, List<Double> label,
String filename) {
try {
FileReader fr = new FileReader(new File(filename));
BufferedReader br = new BufferedReader(fr);
String line = null;
while ((line = br.readLine()) != null) {
String[] datas = line.split(",");
svm_node[] vector = new svm_node[datas.length - 1];
for (int i = 0; i < datas.length - 1; i++) {
svm_node node = new svm_node();
node.index = i + 1;
node.value = Double.parseDouble(datas[i]);
vector[i] = node;
}
nodeSet.add(vector);
double lablevalue = Double.parseDouble(datas[datas.length - 1]);
label.add(lablevalue);
}
} catch (Exception e) {
e.printStackTrace();
}
}
}
调用类:
/**
* SVM支持向量机场景调用类
* @author lyq
*
*/
public class Client {
public static void main(String[] args){
//训练集数据文件路径
String trainDataPath = "C:\\Users\\lyq\\Desktop\\icon\\trainInput.txt";
//测试数据文件路径
String testDataPath = "C:\\Users\\lyq\\Desktop\\icon\\testInput.txt";
SVMTool tool = new SVMTool(trainDataPath);
//对测试数据进行svm支持向量机分类
tool.svmPredictData(testDataPath);
}
}
输入文件的内容:
训练集数据trainInput.txt:
17.6,17.7,17.7,17.7,17.8 17.7,17.7,17.7,17.8,17.8 17.7,17.7,17.8,17.8,17.9 17.7,17.8,17.8,17.9,18 17.8,17.8,17.9,18,18.1 17.8,17.9,18,18.1,18.2 17.9,18,18.1,18.2,18.4 18,18.1,18.2,18.4,18.6 18.1,18.2,18.4,18.6,18.7 18.2,18.4,18.6,18.7,18.9 18.4,18.6,18.7,18.9,19.1 18.6,18.7,18.9,19.1,19.3测试数据集testInput.txt:
18.7,18.9,19.1,19.3,19.6 18.9,19.1,19.3,19.6,19.9 19.1,19.3,19.6,19.9,20.2 19.3,19.6,19.9,20.2,20.6 19.6,19.9,20.2,20.6,21 19.9,20.2,20.6,21,21.5 20.2,20.6,21,21.5,22输出为:
null ------------检验参数----------- ..................* optimization finished, #iter = 452 nu = 0.8563102916247203 obj = -0.8743284941628513, rho = 3.4446523008525705 nSV = 12, nBSV = 9 19.6 19.55027201691905 19.9 19.8455473606175 20.2 20.175593628188604 20.6 20.54041081963737 21.0 20.955769858833488 21.5 21.405899821905447 22.0 21.94590866154817