最优化方法在图像处理中的应用【5】

好吧，我想理解下Convex function(凸函数)。

定义！

A function  f : R^n -> R is convex if domf is a convex set and if for all x,y belongs todom f and theta with 0<=theta<=1, we have

                                     f(theta*x+(1-theta)*y) <= theta*f(x) + (1-theta)*f(y)

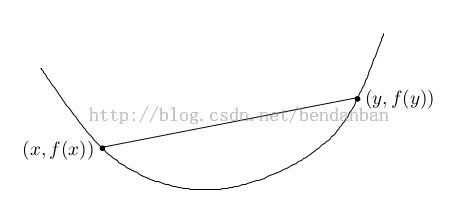
可以用下面的图看看凸函数。

从定义中我们可以得到如下信息：

* 函数f的定义域存在于N维空间。

* 凸函数的定义域是一个凸集。

* 函数满足一个不等式，这个不等式大家都叫Jensen's inequality.

更进一步：

* 凸函数的定义域是个凸集，并且满足Jensen不等式，那么它在定义域的内部一定是连续的，它唯一可能不连续的点只可能在边界上。假设存在不连续点，一定可以推翻Jensen不等式！

其实凸函数还有一些性质，我们不多做研究，继续看凸优化。

一个条件（First-Order Conditions）

Suppose f is differentiable. Then f is convex if and only if

  * dom f is convex

  * f(y) >= f(x) + ∇f(x)^T (y-x)

可知：

* 大前提是f可微！

* 定义域是凸集

* 满足不等式，这个不等式的右边就是多元函数在x点展开的前两项

对于一维函数的情况，我们也可以从图形上理解一下

Second-order conditions

We now assume that f is twice differentiable, that is, its Hessian or second derivative exists at each point in dom f, which is open.

Then f is convex if and only if dom f is convex and its Hessian is positive semidefinite: for all x belongs to dom f, Hessian(f)0

其中的含义是：符号的左边为向量（数学上一般向量指的是列向量）时，表示每个分量大于等于右边的标量。如果这个符号的左边是个矩阵，那么这个符号表示的是左边矩阵的每个特征值都大于等于右边的标量。

二阶可微的函数是凸函数的充分必要条件是：

定义域是凸集，这个函数的Hessian矩阵是非负定矩阵。

说到这里我有两个问题：

1）如果多元函数f是二次可微的，那么它的交叉求导项就一定可以交换顺序么？也就是说，二次可微的多元函数的Hessian矩阵一定是对称的么？

2）实对称矩阵的是非负定阵的充分必要条件可以是矩阵的所有特征值都大于等于0么？

  2.1）首先一个问题是：实对称矩阵一定存在n个实特征值么？

  2.2）每个特征子空间的维数一定等于它所隶属的特征值的重数么？

第一个问题是数学分析问题，第二个问题是代数问题。我会在后面的博文中分开解释。