【数据结构】平衡二叉树之AVL树
平衡二叉排序树
平衡二叉排序树(Balanced Binary Sort Tree),上一篇博客【数据结构】二叉排序树BST讲了BST,并且在最后我们说BST上的操作不会超过O(h),既然树高这么重要,那么BBST的研究就是为了使得树的深度在可接受的范围内渐近意义下达到O(lgn)
n个节点组成的二叉树,其高度为lgn取下限时,这棵树是理想平衡的,满足这样条件的树只有完全二叉树和满二叉树,这样的要求未免太苛刻,并且实际中没有意义。
适度平衡:保证树高在渐近意义上不超过O(lgn)适度平衡的树也称作平衡二叉树。
并且我们知道,任何平衡的二叉树在经过一系列的插入删除操作后可能会不平衡,因此任何一种BBST都包含了界定平衡的标准和一系列重平衡(rebalance)的方法。
平衡二叉排序树包括:AVL树,红黑树,伸展树等
AVL树
AVL树仅仅是平衡二叉树的一种,它是最经典的最早发明的一种BBST(貌似严蔚敏老师的书上说平衡二叉树又称AVL树),AVL树由G.M. Adelson-Velsky 和 E.M. Landis发明。AVL定义适度平衡的标准:
定义平衡因子(BalanceFactor):BF(node) = height(lchild(node)) - height(rchild(node))
对所有的节点node,有|BF(node)| <= 1
一系列的重平衡方法:旋转操作
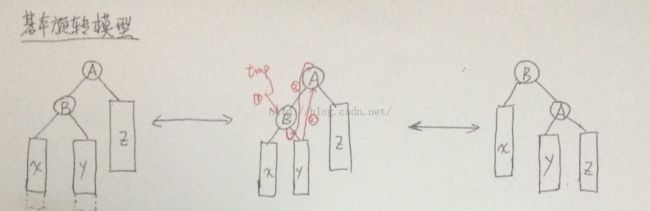
基本的旋转操作如下图所示
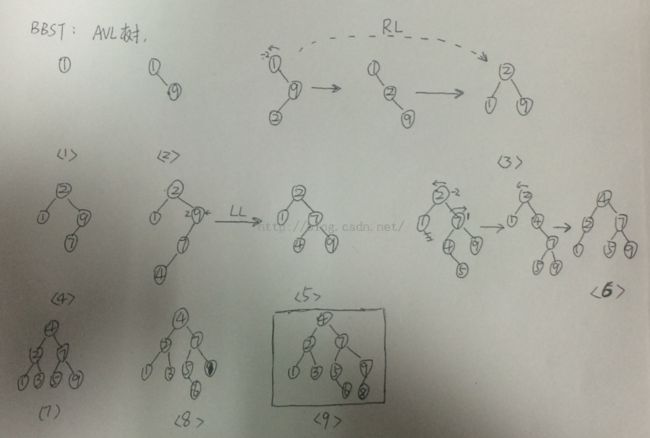
根据不同的情形又分为四种情况
相关算法
1.返回某个结点的高度height我们设定当结点为null时的高度为-1,其余情况的高度由每个结点自己维护。
private int height(BinaryTreeNode node) {
if (node == null) {
return -1;
} else {
return node.height;
}
}
2.返回某个结点的平衡因子
平衡因子等于左子树高度减右子树高度
private int balance(BinaryTreeNode node) {
if (node == null)
return 0;
return height(node.lchild) - height(node.rchild);
}
3.左旋LL
按照图示顺序分三步,将tmp作为最终的根结点返回。
需要额外做的工作包括对父结点改变了的结点赋新的parent,更新高度,最终返回的结点的父亲节点一定要在调用处设置!!// LL 将node结点左旋,node是最小不平衡子树的根
public BinaryTreeNode leftRotate(BinaryTreeNode node) {
BinaryTreeNode tmp = node.lchild;
tmp.parent = null;
node.lchild = tmp.rchild;
if (tmp.rchild != null)
tmp.rchild.parent = node;
tmp.rchild = node;
node.parent = tmp;
// 更新高度,包括是node和node.rchild
node.height = Math.max(height(node.lchild), height(node.rchild)) + 1;
tmp.height = Math.max(height(tmp.lchild), node.height) + 1;
return tmp;
}
4.双旋LR
分两步即可,先对结点的左子树进行左旋操作,再对该结点进行右旋操作,要注意保存第一次返回的结点的父亲结点!!
public BinaryTreeNode leftRightRotate(BinaryTreeNode node) {
node.lchild = rightRotate(node.lchild);
node.lchild.parent = node; // 父结点赋值!!
return leftRotate(node);
}
5.返回待旋转的结点的旋转类型
private RotateType rotateType(BinaryTreeNode node) {
if (balance(node) < -1) {
if (balance(node.rchild) > 0) {
return RotateType.RL;
} else {
return RotateType.RR;
}
} else { // >1
if (balance(node.lchild) < 0) {
return RotateType.LR;
} else {
return RotateType.LL;
}
}
}
6.用以node为顶点旋转过后的树来代替node这棵子树
区别之前用的replace函数void replace(BinaryTreeNode node1, BinaryTreeNode node2)
将结点A旋转后,A的父结点左右孩子都已经变了,因此要先将他的父结点保存下来以便将旋转后的子树往它后面挂,所以对该函数的调用不等于调用replace(node,leftRotate(node),type);
// 拼接旋转后的子树:用以node为定点旋转过后的树来代替node这棵子树
private void replaceNode(BinaryTreeNode node,
RotateType type) {
BinaryTreeNode tmpParent = node.parent;
BinaryTreeNode rotateNode = null;
switch (type) {
case LL:
rotateNode = leftRotate(node);
break;
case RR:
rotateNode = rightRotate(node);
break;
case LR:
rotateNode = leftRightRotate(node);
break;
case RL:
rotateNode = rightLeftRotate(node);
break;
}
if (tmpParent == null) {
root = rotateNode;
rotateNode.parent = null; //父结点赋值非常关键!!
} else if (tmpParent.rchild == node) {
tmpParent.rchild = rotateNode;
rotateNode.parent = root; //父结点赋值非常关键!!
} else {
tmpParent.lchild = rotateNode;
rotateNode.parent = root; //父结点赋值非常关键!!
}
}
插入和删除
有了上面一些基本的函数,就可以进行下面的两个重要操作:插入/删除结点
插入节点
当插入一个结点可能会造成他的祖父结点失衡,进而曾祖父结点也会失衡等等一直往上延伸。这么看来插入操作似乎很复杂?事实并不是这样,尽管这样,我们却不需要从下往上挨个调整结点至平衡。因为好消息是只要把从下往上的第一个失衡的结点所构成的子树重平衡就能保证其之上的所有结点平衡。这里的第一个失衡的结点所构成的子树称为最小不平衡子树。调整最小不平衡子树至重平衡,它的高度和插入结点之前相比未变,因此也不会影响到更上层的结点。这样只需要有限步操作即可重平衡,复杂度为O(1)。这里每插入一个节点都要更新已存在的结点的高度!插入的实现和BST里面一样,只是要更新结点高度
private BinaryTreeNode insertRecurAVL(BinaryTreeNode root,BinaryTreeNode insertNode) {
if (this.root == null) {
this.root = root = insertNode;
} else if (insertNode.data < root.data && root.lchild == null) {
root.lchild = insertNode;
insertNode.parent = root;
} else if (insertNode.data >= root.data && root.rchild == null) {
root.rchild = insertNode;
insertNode.parent = root;
} else {
if (insertNode.data < root.data && root.lchild != null)
insertRecurAVL(root.lchild, insertNode);
if (insertNode.data >= root.data && root.rchild != null)
insertRecurAVL(root.rchild, insertNode);
}
// 更新高度!
root.height = Math.max(height(root.lchild), height(root.rchild)) + 1;// 放在这里的位置很重要
return insertNode;
}
于是插入节点后对其进行检查重平衡的代码如下,基本思路是将新的结点插入到对应的位置,然后从他开始往上走,直到遇到第一个不平衡的结点,也就是最小不平衡子树,然后旋转这个结点让其恢复平衡后来替换该结点。
public void insertAVL(BinaryTreeNode insertNode) {
BinaryTreeNode node = insertRecurAVL(root, insertNode);
// 调整最小不平衡子树
while (node != null && balance(node) > -2 && balance(node) < 2) {
node = node.parent;
} // 跳出循环时,node为null 或者node不平衡
if (node != null) {
// 确定何种类型的旋转
RotateType type = rotateType(node);
replaceNode(node, type);
}
}
从数组创建一棵BBST的过程也可以通过insert操作循环的插入即可。
删除结点
删除某个节点只可能导致他的父亲节点失衡,因为,如果我们删除最深的那条子树,那么不会失衡,所以产生失衡只可能是由于删除了短的子树上的结点,这样对外界来说,该结点的父亲所在的子树的高度未变,于是上面的结点的平衡性也不会改变。那么删除操作只需要重平衡它的父结点吗?事实上,删除一个结点他的父亲如果发生了失衡,那么当让其父亲节点重平衡后,局部子树的高度减少了,因此失衡的情况可能继续往上传递,最差情况下一直传递到根,于是删除的复杂度为O(lgn)。其实也就是因为这个原因,AVL树用的不多,SGI的STL中都未实AVL树,仅仅实现了红黑树
// 删除AVL树中的结点
public void deleteAVL(BinaryTreeNode node) {
System.out.println(node.toString());
BinaryTreeNode predecessorOfnode = null;
if (node.lchild == null) { // 左子树为空,只需要移植右子树
replace(node, node.rchild);
} else if (node.rchild == null) {
replace(node, node.lchild);
} else {
predecessorOfnode = predecessor(node);
replace(node, node.lchild);
predecessorOfnode.rchild = node.rchild;
node.rchild.parent = predecessorOfnode;
predecessorOfnode.height = Math.max(height(predecessorOfnode.lchild), height(node.rchild)) + 1;
}
// 调整平衡
// 只需要从删除的结点的前驱开始依次向上判断
BinaryTreeNode nodetmp = predecessorOfnode;
while (nodetmp != null) {
BinaryTreeNode tmp = nodetmp.parent; // 下面的旋转操作会改变nodetmp的父结点,所以提前保存下来!!
if (balance(nodetmp) < -1 || balance(nodetmp) > 1) {
// 不平衡
RotateType type = rotateType(nodetmp);
replaceNode(nodetmp, type);
}
nodetmp = tmp;
}
}
AVL树的实现
其中使用的BinaryTreeNode比起之前多了一个height字段,用来保存每个节点的高度,结点为null时,高度为-1
public class AVLTree extends BinarySearchTree {
public enum RotateType {
LL, RR, LR, RL
};
@Override
public void createTree(int[] array) {
// 从一个数组创建二叉搜索树
for (int i : array) {
insertAVL(new BinaryTreeNode(i));
}
}
// 删除AVL树中的结点
public void deleteAVL(BinaryTreeNode node) {
BinaryTreeNode predecessorOfnode = null;
if (node.lchild == null) { // 左子树为空,只需要移植右子树
replace(node, node.rchild);
} else if (node.rchild == null) {
replace(node, node.lchild);
} else {
predecessorOfnode = predecessor(node);
replace(node, node.lchild);
predecessorOfnode.rchild = node.rchild;
node.rchild.parent = predecessorOfnode;
predecessorOfnode.height = Math.max(
height(predecessorOfnode.lchild), height(node.rchild)) + 1;
}
// 调整平衡
// 只需要从删除的结点的前驱开始依次向上判断
BinaryTreeNode nodetmp = predecessorOfnode;
while (nodetmp != null) {
BinaryTreeNode tmp = nodetmp.parent; // 下面的旋转操作会改变nodetmp的父结点,所以提前保存下来!!
if (balance(nodetmp) < -1 || balance(nodetmp) > 1) {
// 不平衡
RotateType type = rotateType(nodetmp);
replaceNode(nodetmp, type);
}
nodetmp = tmp;
}
}
// 插入节点 并处理可能的不平衡结点
public void insertAVL(BinaryTreeNode insertNode) {
BinaryTreeNode node = insertRecurAVL(root, insertNode);
while (node != null && balance(node) > -2 && balance(node) < 2) {
node = node.parent;
} // 跳出循环时,node为null 或者node不平衡
if (node != null) {
// 确定何种类型的旋转
RotateType type = rotateType(node);
replaceNode(node, type);
}
}
// 递归的插入结点,同时更新每个结点的高度
private BinaryTreeNode insertRecurAVL(BinaryTreeNode root,
BinaryTreeNode insertNode) {
if (this.root == null) {
this.root = root = insertNode;
} else if (insertNode.data < root.data && root.lchild == null) {
root.lchild = insertNode;
insertNode.parent = root;
} else if (insertNode.data >= root.data && root.rchild == null) {
root.rchild = insertNode;
insertNode.parent = root;
} else {
if (insertNode.data < root.data && root.lchild != null)
insertRecurAVL(root.lchild, insertNode);
if (insertNode.data >= root.data && root.rchild != null)
insertRecurAVL(root.rchild, insertNode);
}
root.height = Math.max(height(root.lchild), height(root.rchild)) + 1;// 放在这里的位置很重要
return insertNode;
}
// 拼接旋转后的子树:用以node为定点旋转过后的树来代替node这棵子树
private void replaceNode(BinaryTreeNode node, RotateType type) {
BinaryTreeNode tmpParent = node.parent;
BinaryTreeNode rotateNode = null;
switch (type) {
case LL:
rotateNode = leftRotate(node);
break;
case RR:
rotateNode = rightRotate(node);
break;
case LR:
rotateNode = leftRightRotate(node);
break;
case RL:
rotateNode = rightLeftRotate(node);
break;
}
if (tmpParent == null) {
root = rotateNode;
rotateNode.parent = null; // 父结点赋值非常关键!!
} else if (tmpParent.rchild == node) {
tmpParent.rchild = rotateNode;
rotateNode.parent = root; // 父结点赋值非常关键!!
} else {
tmpParent.lchild = rotateNode;
rotateNode.parent = root; // 父结点赋值非常关键!!
}
}
// 获取待旋转结点的旋转类型
private RotateType rotateType(BinaryTreeNode node) {
if (balance(node) < -1) {
if (balance(node.rchild) > 0) {
return RotateType.RL;
} else {
return RotateType.RR;
}
} else { // >1
if (balance(node.lchild) < 0) {
return RotateType.LR;
} else {
return RotateType.LL;
}
}
}
// 返回结点的平衡因子 返回值为-2 -1 0 1 2
private int balance(BinaryTreeNode node) {
if (node == null)
return 0;
return height(node.lchild) - height(node.rchild);
}
// 返货某个节点的高度
private int height(BinaryTreeNode node) {
if (node == null) {
return -1;
} else {
return node.height;
}
}
// 将node结点左旋,node是最小不平衡子树的根
// RR
public BinaryTreeNode rightRotate(BinaryTreeNode node) {
BinaryTreeNode tmp = node.rchild;
tmp.parent = null;
node.rchild = tmp.lchild;
if (tmp.lchild != null)
tmp.lchild.parent = node;
tmp.lchild = node;
node.parent = tmp;
// 更新高度,包括是node和node.rchild
node.height = Math.max(height(node.lchild), height(node.rchild)) + 1;
tmp.height = Math.max(height(tmp.rchild), node.height) + 1;
return tmp;
}
// 将node结点左旋,node是最小不平衡子树的根
// LL
public BinaryTreeNode leftRotate(BinaryTreeNode node) {
BinaryTreeNode tmp = node.lchild;
tmp.parent = null;
node.lchild = tmp.rchild;
if (tmp.rchild != null)
tmp.rchild.parent = node;
tmp.rchild = node;
node.parent = tmp;
// 更新高度,包括是node和node.rchild
node.height = Math.max(height(node.lchild), height(node.rchild)) + 1;
tmp.height = Math.max(height(tmp.lchild), node.height) + 1;
return tmp;
}
// LR
public BinaryTreeNode leftRightRotate(BinaryTreeNode node) {
node.lchild = rightRotate(node.lchild);
node.lchild.parent = node;
return leftRotate(node);
}
// RL
public BinaryTreeNode rightLeftRotate(BinaryTreeNode node) {
node.rchild = leftRotate(node.rchild);
node.rchild.parent = node;
return rightRotate(node);
}
}
测试
仍然使用上篇博客中创建BST的数组int[] array = { 1, 9, 2, 7, 4, 5, 3, 6, 8 };
public static void main(String[] args) {
AVLTree avl = new AVLTree();
int[] array = { 1, 9, 2, 7, 4, 5, 3, 6, 8 };
avl.createTree(array);
System.out.println("层序打印结点和其高度");
avl.levelOrderH();
System.out.println("删除结点7得到的层序遍历");
avl.deleteAVL(avl.search(avl.root, 7));
avl.levelOrderH();
}
输出
层序打印结点和其高度 4 2 7 1 3 5 9 6 8 删除结点7得到的层序遍历 4 2 8 1 3 5 9 6可以发现,前面将该数组创建成BST,树高非常高,现在将其创建成AVL树,发现非常的平衡,树高比之前低多了。并且在动态插入和删除过程中始终能维护树的平衡性。
分析
分析该数组的创建和删除结点的过程
上述的代码在通过该数组创建AVL树的过程如下
删除结点7的过程如下图
后记
可能最后的代码才200行左右,但是编些难度不小,比起写个应用分分钟上千行代码难多了,改bug改了一个晚上。由于我在这里每个节点保存父结点,所以好几次忘记给父结点赋值,旋转的时候,由于指针变化也会产生好多问题,编写代码的过程中遇到导致错误的地方都标注在代码中。