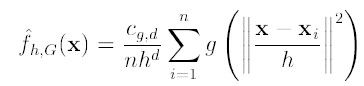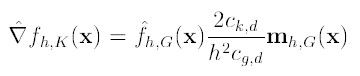机器学习算法原理与实践（二）、meanshift算法图解以及在图像聚类、目标跟踪中的应用
【原创】Liu_LongPo 转载请注明出处
【CSDN】http://blog.csdn.net/llp1992
最近在关注跟踪这一块的算法，对于meanshift的了解也是来自论文和博客，本博客将对meanshift算法进行总结，包括meanshift算法原理以及公式推导，图解，图像聚类，目标跟踪中的应用以及优缺点总结。
算法原理
meanshift算法其实通过名字就可以看到该算法的核心，mean（均值），shift（偏移），简单的说，也就是有一个点 
,它的周围有很多个点 
我们计算点 移动到每个点 所需要的偏移量之和，求平均，就得到平均偏移量，（该偏移量的方向是周围点分布密集的方向）该偏移量是包含大小和方向的。然后点 就往平均偏移量方向移动，再以此为新的起点不断迭代直到满足一定条件结束。
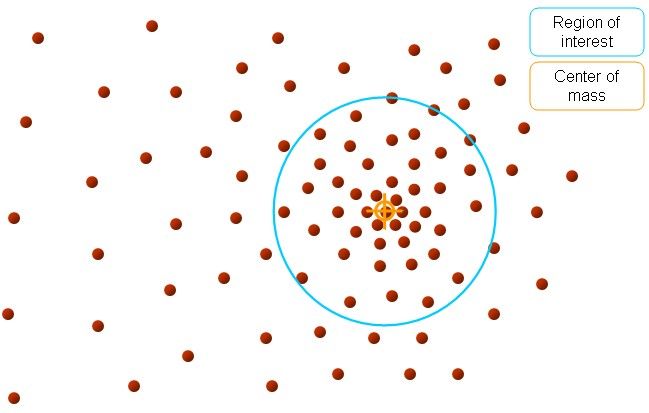
图解如下:
中心点就是我们上面所说的 周围的小红点就是 黄色的箭头就是我们求解得到的平均偏移向量。那么图中“大圆圈”是什么东西呢？我们上面所说的周围的点 周围是个什么概念？总的有个东西来限制一下吧。那个“圆圈”就是我们的限制条件，或者说在图像处理中，就是我们搜索迭代时的窗口大小。不过在opencv中，我们一般用的是矩形窗口，而且是图像，2维的。这里其实不是圆，而是一个高维的球。
步骤1、首先设定起始点 ，我们说了，是球，所以有半径 
， 所有在球内的点就是 , 黑色箭头就是我们计算出来的向量 , 将所有的向量 进行求和计算平均就得到我们的meanshift 向量，也就是图中黄色的向量。
接着，再以meanshift向量的重点为圆心，再做一个高维的球，如下图所示，重复上面的步骤，最终就可以收敛到点的分布中密度最大的地方
最终结果如下：
数学推导
给定d维空间Rd的n个样本点 ,i=1,…,n,在空间中任选一点x，那么 meanshift 向量的基本定义如下：
其中 
是一个半径为 的高维度区域。定义如下：
表示在这n个样本点xi中,有k个点落入 区域中.
然后，我们对meanshift向量进行升级，加入核函数（比如高斯核），则meanshift算法变为:
解释一下K()核函数，h为半径， 
为单位密度，要使得上式f得到最大，最容易想到的就是对上式进行求导，的确meanshift就是对上式进行求导.
令 
, 则我们可以得到：
由于我们使用的是高斯核，所以第一项等于
第二项就相当于一个meanshift向量的式子:
则上述公式可以表示为：
图解公式的结构如下：
当然，我们求得meanshift向量的时候，其密度最大的地方也就是极值点的地方，此时梯度为0，也就是
,当且仅当
的时候成立，此时我们就可以得到新的原点坐标：
以上就是公式推导，建议看懂走一遍。参考自
http://www.cnblogs.com/liqizhou/archive/2012/05/12/2497220.html
实际项目中，meanshift的算法流程是：
1、选取中心点
2、计算，如果
meanshift在图像处理中的 聚类，跟踪中的应用
上面我们可看到，meanshift 算法每一步其实都是往密度最大的方向走，空间中的点的分布的密度刚好就可以运用到meanshift算法中，而一幅图像都是由密密麻麻的像素点组成，怎么利用密度分布的不一致来进行聚类呢？
首先我们想到的依旧是距离，距离越近，越有可能被分到同一类中。因此我们利用点的概率密度，也就是
离圆点
然后我们又可以想到，分到同一类的颜色一般都是比较接近的，所以再定义颜色概率密度：
与圆点
然后，每个点的概率密度分布可以由一下公式得到：
其中：
代表空间位置的信息，离远点越近，其值就越大，
表示颜色信息，颜色越相似，其值越大。
接下来就可以运 meanshift 算法进行聚类。
meanshift算法目标跟踪
在opencv中已经有库函数可以调用了：
int cvMeanShift(const CvArr* prob_image,CvRect window,CvTermCriteria criteria,CvConnectedComp* comp );查看API可以知道，调用该函数时，需要输入的图像是反向投影图，什么是反向投影图，简单介绍一下：
图像的反向投影图是用输入图像的某一位置上像素值（多维或灰度）对应在直方图的一个bin上的值来代替该像素值，所以得到的反向投影图是单通的。用统计学术语，输出图像象素点的值是观测数组在某个分布（直方图）下的概率。
不懂？用例子说明一下：
- (1)例如灰度图像如下
Image=
0 1 2 3
4 5 6 7
8 9 10 11
8 9 14 15
- (2)该灰度图的直方图为（bin指定的区间为[0,3)，[4,7)，[8,11)，[12,16)）
Histogram=
4 4 6 2
- (3)反向投影图
Back_Projection=
4 4 4 4
4 4 4 4
6 6 6 6
6 6 2 2
例如位置(0,0)上的像素值为0，对应的bin为[0,3)，所以反向直方图在该位置上的值这个bin的值4。
这下懂了吧，其实就是一张图像的像素密度分布图，而我们的meanshift算法本身就是依靠密度分布进行工作的，找到密度分布最大的地方。所以就很容易理解这个输入参数了。
半自动跟踪思路：输入视频，用画笔圈出要跟踪的目标，然后对物体跟踪。
用过opencv的都知道，这其实是camshiftdemo的工作过程。
第一步：选中物体，记录你输入的方框和物体。
第二步：求出视频中有关物体的反向投影图。
第三步：根据反向投影图和输入的方框进行meanshift迭代，由于它是向重心移动，即向反向投影图中概率大的地方移动，所以始终会移动到目标上。
第四步：然后下一帧图像时用上一帧输出的方框来迭代即可。
全自动跟踪思路：输入视频，对运动物体进行跟踪。
第一步：运用运动检测算法将运动的物体与背景分割开来。
第二步：提取运动物体的轮廓，并从原图中获取运动图像的信息。
第三步：对这个信息进行反向投影，获取反向投影图。
第四步：根据反向投影图和物体的轮廓（也就是输入的方框）进行meanshift迭代，由于它是向重心移 动，即向反向投影图中概率大的地方移动，所以始终会移动到物体上。
第五步：然后下一帧图像时用上一帧输出的方框来迭代即可。
总结
meanShift算法用于视频目标跟踪时，其实就是采用目标的颜色直方图作为搜索特征，通过不断迭代meanShift向量使得算法收敛于目标的真实位置，从而达到跟踪的目的。
在目标跟踪中：meanshift有以下几个优势：
（1）算法计算量不大，在目标区域已知的情况下完全可以做到实时跟踪；
（2）采用核函数直方图模型，对边缘遮挡、目标旋转、变形和背景运动不敏感。
同时，meanShift算法也存在着以下一些缺点：
（1）缺乏必要的模板更新；
（2）跟踪过程中由于窗口宽度大小保持不变，当目标尺度有所变化时，跟踪就会失败；
（3）当目标速度较快时，跟踪效果不好；
（4）直方图特征在目标颜色特征描述方面略显匮乏，缺少空间信息；
由于其计算速度快，对目标变形和遮挡有一定的鲁棒性，其中一些在工程实际中也可以对其作出一些改进和调整如下：
（1）引入一定的目标位置变化的预测机制，从而更进一步减少meanShift跟踪的搜索时间，降低计算量；
（2）可以采用一定的方式来增加用于目标匹配的“特征”；
（3）将传统meanShift算法中的核函数固定带宽改为动态变化的带宽；
（4）采用一定的方式对整体模板进行学习和更新；