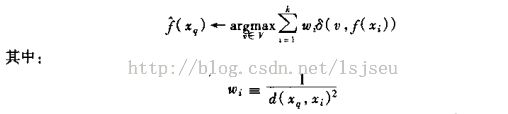机器学习笔记之K近邻算法
基于实例的学习方法
K近邻算法其实是一种基于实例的学习算法。基于实例的学习方法只是简单的把样例存储起来。把这些实例中泛化的工作被推迟到必须分类实例的时候。每当学习器遇到一个新的查询实例,它分析这个新实例与以前存储的实例的关系。并据此把一个目标函数值赋给新的实例。
基于实例的学习方法包括K近邻算法和局部加权回归。本文只讲K近邻算法。
基于实例学习方法与其他算法相比:基于实例方法可以为不同的待分类查询实例建立不同的目标函数逼近。事实上,很多技术只是建立目标函数的局部逼近,将其运用于与新查询邻近的实例,而从不在整个实例空间上建立表现良好的逼近。当目标复杂但却用这种不太复杂的局部逼近时,具有显著优势。(k较小的时候,模型比较复杂,k较大的时候,模型比较简单。我们区域选择模型简单的分类,奥卡姆剃刀)
基于实例学习方法缺点:分类新实例开销太大,K值不好选。
K-近邻算法
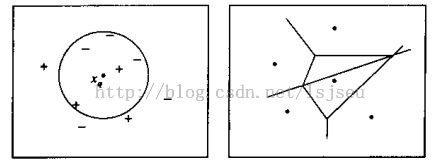
该算法假定所有的实例对应于n维空间总的点。一个实例的最近邻是根据标准欧式距离定义的(欧式距离计算)。在K近邻计算中,目标函数值可以使离散的也可以实值的。
(1)离散情况下:用距离样例最近的K个训练样例最普遍的值估计当前样例的值。最普可以是哪种样本值占比例最大。
(2)连续情况下:用距离样例最近的K个训练样例平均值估计当前样例的值。
距离加权算法
对于k近邻算法的一个明显改进是对K个近邻的贡献加权。根据他们相对查询点的距离,将较大的权值赋给较近的近邻。
(1)可用距离平方的倒数作权值:
(2)上面这种方法有个问题,恰好匹配当前样例点将导致分母无穷大。可以用下面这个公式进行加权:
注:上面只考虑K个近邻去分类查询点,其实也可以全部样例,只不过距离远的点,权值很小(趋于0)。这样我们定义如果运用全部样例去分类一个新的实例叫作全局法。只用K个近邻点,叫局部法。
K-近邻算法优缺点
(1)抗噪声能力强:通过对近邻加权可以消除孤立噪声。
(3)维度灾难:k-近邻算法在计算距离的时候,考虑实例的所有属性。可能分类仅由2个属性决定,这中情况下属性的相似性度量会误导k-近邻算法的分类。
解决办法:(1)属性加权;(2)剔除不相关的属性。
后记:
推荐一下本博客的两篇文章:K近邻与kd树,从kd树谈到SIFT算法