排序算法c语言描述---归并排序

排序算法系列学习，主要描述冒泡排序，选择排序，直接插入排序，希尔排序，堆排序，归并排序，快速排序等排序进行分析。

文章规划：

一。通过自己对排序算法本身的理解，对每个方法写个小测试程序。 具体思路分析不展开描述。

二。通过《大话数据结构》一书的截图，详细分析该算法 。

 在此，推荐下程杰老师的《大话数据结构》一书，当然不是打广告，只是以一名读者的身份来客观的看待这本书，确实是通俗易懂，值得一看。

ps：一个较为详细的学习链接 http://blog.csdn.net/MoreWindows/article/category/859207

六。归并排序

一。个人理解

归并（Merge）排序法是将两个（或两个以上）有序表合并成一个新的有序表，即把待排序序列分为若干个子序列，每个子序列是有序的。然后再把有序子序列合并为整体有序序列。

所以归并排序的核心在于先分解，再合并。

其基本思路就是将数组分成二组A，B，如果这二组组内的数据都是有序的，那么就可以很方便的将这二组数据进行排序。

那么如何让这二个数组组内数据有序呢？

可以将A，B组各自再分成二组。依次类推，当分出来的小组只有一个数据时，可以认为这个小组组内已经达到了有序，然后再合并相邻的二个小组就可以了。这样通过先递归的分解数列，再合并数列就完成了归并排序。

好了，下面就是具体操作过程：

1) 将n个元素分成各含n/2个元素的子序列

2)用归并排序法对这两个子序列递归地排序

3)合并这两个已经排序好的子序列得到排序结果

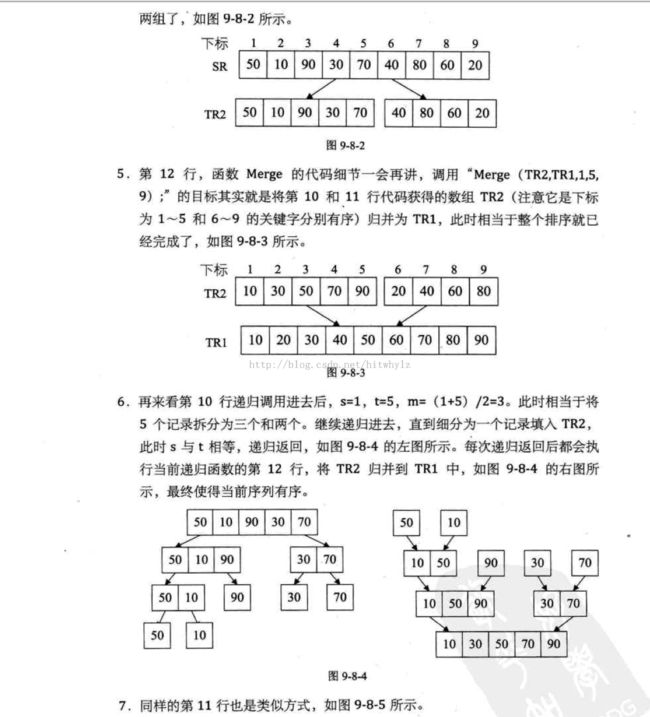
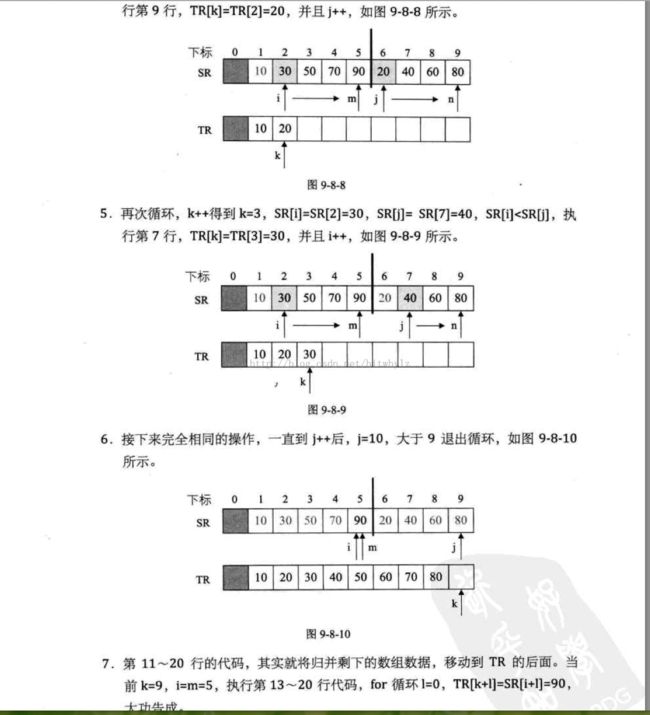
归并排序的大致内容就是这样，如果有什么不理解，可以具体看下面的《大话数据结构》一书截图，具体不再重复。

直接上代码。

#include<stdio.h>

#define Max_ 10
// 打印结果
void Show(int  arr[], int n)
{
    int i;
    for ( i=0; i<n; i++ )
        printf("%d  ", arr[i]);
    printf("\n");
}

// 归并排序中的合并算法
void Merge(int array[], int left, int m, int right)
{
    int aux[Max_] = {0};  // 临时数组 （若不使用临时数组，将两个有序数组合并为一个有序数组比较麻烦）
    int i; //第一个数组索引
    int j; //第二个数组索引
    int k; //临时数组索引
    
    for (i = left, j = m+1, k = 0; k <= right-left; k++) // 分别将 i, j, k 指向各自数组的首部。
    {
        //若 i 到达第一个数组的尾部，将第二个数组余下元素复制到 临时数组中
        if (i == m+1)
        {
            aux[k] = array[j++];
            continue;
        }
        //若 j 到达第二个数组的尾部，将第一个数组余下元素复制到 临时数组中
        if (j == right+1)
        {
            aux[k] = array[i++];
            continue;
        }
        //如果第一个数组的当前元素 比 第二个数组的当前元素小，将 第一个数组的当前元素复制到 临时数组中
        if (array[i] < array[j])
        {
            aux[k] = array[i++];
        }
        //如果第二个数组的当前元素 比 第一个数组的当前元素小，将 第二个数组的当前元素复制到 临时数组中
        else
        {
            aux[k] = array[j++];
        }
    }
    
    //将有序的临时数组 元素 刷回 被排序的数组 array 中，
    //i = left , 被排序的数组array 的起始位置
    //j = 0， 临时数组的起始位置
    for (i = left, j = 0; i <= right; i++, j++)
    {
        array[i] = aux[j];
    }
}

// 归并排序
void MergeSort(int array[], int start, int end)
{
    if (start < end)
    {
        int i;
        i = (end + start) / 2;
        // 对前半部分进行排序
        MergeSort(array, start, i);
        // 对后半部分进行排序
        MergeSort(array, i + 1, end);
        // 合并前后两部分
        Merge(array, start, i, end);
    }
}

int main()
{   //测试数据
    int arr_test[Max_] = { 8, 4, 2, 3, 5, 1, 6, 9, 0, 7 };
    //排序前数组序列
    Show( arr_test, Max_ );
    MergeSort( arr_test, 0, Max_-1 );
    //排序后数组序列
    Show( arr_test, Max_ );
    return 0;
}

二。 《大话数据结构》一书截图分析

注：本文仅为分享知识，绝无商业用途。

如果以该种形式分享知识造成不必要的纠纷，还请第一时间告知。