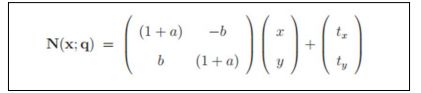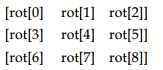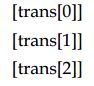Mastering OpenCV with Practical Computer Vision Projects_full 章节翻译-7
感谢翻译,译文原链接http://94it.net/a/jingxuanboke/2014/0228/255204.html 学习了
Chapter 7:3D Head Pose Estimation Using AAM and POSIT
一个好的计算机视觉算法如果没有伟大健壮的功能以及广泛的普遍化和一个坚实的数学基础是不完整的。所有的这些优点伴随着主要由TimCootes开发的主动表观模型(Active Appearance Models)。这一章将教给你怎样使用OpenCV创建一个你自己的主动表观模型以及怎样在一个给出的图像帧中使用它搜索模型所在的最邻近位置。而且你将学习如何使用POSIT算法和如何在你的”posed”图像中拟合你的3D模形。使用这些工具,你将能够实时地在一个视频中跟踪一个3D模型。不是很棒吗?尽管例子的焦点在于头部姿态,事实上,任何可变模型可以采用同样的方法。
当你读这些部分,你将碰到下列主题:
1、主动表观模型概述
2、主动形状模型概述
3、模型实例化——运行主动表观模型
4、AAM搜索和匹配(或拟合,fitting)
5、POIST
下面的列表阐述了本章中你将要碰到的术语:
1、主动表观模型(AAM):一个对象的模型,包含着对象形状和纹理的统计信息。它是捕获对象形状和纹理变化的一个强大的方法。
2、主动形状模型(ASM):对象形状的统计模型。它对于学习形状变化非常有用。
3、主成分分析(PCA):一个正交线性变换。它将数据转换到一个新的坐标系统,满足:数据任何投影产生的最大方差将位于第一个坐标(称为第一个主成分),第二个最大的方差位于第二个坐标上,等等。这个过程通常用在降维。当最初的问题减少了维数,我们可以使用一个更快的匹配(faster-fitting)算法。
4、三角剖分(DT):对于平面上的一组点P,它是一个三角剖分,以使得在三角剖分中P中的任何点都不会在任何三角形的外接圆内。它倾向于避免紧瘦的三角形。三角剖分用来纹理的映射。
5、仿射变换:任何转换都可以用一个矩阵相乘跟着一个矢量的加法的形式来表示。仿射变换可以用来纹理的映射。
6、Pose from Orthography and Scaling with Iterations(POSIT):一个执行3D姿态估计的计算机视觉算法。
主动表观模型概述——Active Appearnce Models overview
简单地说,主动表观模型是一个组合纹理和形状耦合到一个有效的搜索算法的参数化模型,它可以准确的告诉我们一个模型在一个图像帧中的位置以及如何定位于这个位置。为了做到这一点,我们将以主动形状模型部分开始并且将看到它们与标记的位置紧密关联。主成分分析和一些实践经验将在下面的部分更好的描述。那时,我们将能够从OpenCV的Delaunay函数的获得一些帮助并且学习一些三角剖分。从那起,在三角纹理变换部分,我们将发展到应用分段的仿射变换并且我们可以从一个对象的纹理中获得信息。
当我们获得足够的背景来建立一个好的模型,我们可以在模型的实例部分应用这些技术。然后,我们将能够通过AAM搜索和匹配来解决反问题(the inverse problem)。对于2D或许甚至3D图像匹配,这些算法本身已经是非常有用的算法。但是当我们能够运用这些算法时,为什么不把它联系到POSIT——3D模型拟合的另一个坚如磐石的算法呢?投入到POSIT部分(Diving into the POSIT section)我们将获得足够的背景来和它(算法)在OpenCV中一起工作,然后,在下面的部分,我们将学习如何耦合它的一个头部模型。这样,我们可以使用一个3D模型来拟合已匹配的2D图像帧。并且如果一个强烈的读者想知道这将把我们带到哪里,这正是用一个帧到帧的方式组合AAM和Posit,通过可变模型的检测来得到一个实时的3D跟踪。这些细节将在来至网络相机或者视频文件的跟踪部分涉及到。
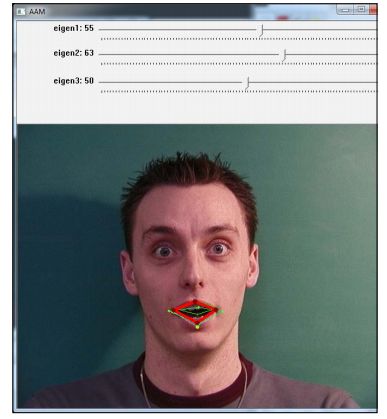
据说一个照片顶一千个词。想象一下如果我们获得了N个照片。这样,我们先前提到的内容可以在下面截图中简单的跟踪。
本章算法的概述:给出一个图像(先前截图的左上图像),我们可以使用主动表观搜索算法来找到人类头部的2D姿态。截图中右上边的图像展示了先前训练好的用在搜索算法中的一个主动表观模型。找到一个姿态之后,POSIT可以用来推广这个结果到3D姿态。如果这个过程应用到了一个视频序列,将通过检测获得3D跟踪。
主动形状模型——Active Shape Models
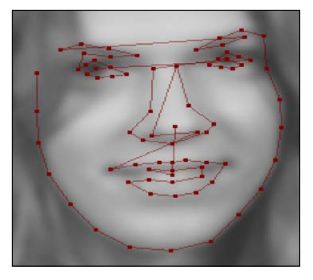
像先前提到的,AAM需要一个形状模型,这个角色通过ASM扮演(Active Shape Models)。在接下来的部分中,我们将创建一个ASM,它是形状变化的统计模型。这个形状模型通过形状变化的组合产生。需要一个标记过的图像训练集,就像文章形状模型——他们的训练和应用(Active Shape Models-Their Training and Application )中描述的那样。为了建立一个人脸形状模型,一些标记了人脸关键位置点的图像用来概述主要的特征。下面的截图展示了一个这样的例子:
一个人脸上有76个标记,这来至于MUCT数据库。这些标记通常是手工标记的并且概述了一些人脸特征,例如嘴的轮廓,鼻子,眼睛,眉毛和脸的形状,因为这些特征易于跟踪。
注释:
Procrustes分析:统计形状分析的一个形式,常用于分析一组形状的分布。Procrustes叠加是通过最优地平移,旋转和一致地缩放对象来执行的。
如果我们有先前提到的图像集,我们可以产生一个形状变化的统计模型。因为标记点在对象上描述了这个对象的形状,如果需要的话,首先我们使用Procrustes分析将这些点集对齐到一个坐标框架,并且通过一个矢量x表示每一个形状。然后,我们对数据应用主成分分析。那么我们可以使用下面的公式估算任何实例:
x = x + Ps bs
在前面的公式中,x是均值形状,Ps是一组变化的正交模式,bs是一组形状参数。好的,为了更好的理解,我们将在本节的剩余部分创建一个简单的应用,这将为我们展示如何处理PCA和形状模型。
使用PCA究竟为什么?因为当减少我们模型参数的数量时,PCA能真正的帮助我们。在本章的后面,我也将看到当在一个给定的图像中搜索它时,它给我们的帮助是多大。下面的引用来至于一个网页:
当人们从目标的丰富信息视点观察时,PCA可以为用户提供一个低维图像——对象的一个“影子”。通过仅使用前几个少量主成分就可以完成,这使得转换后的数据维数减少。
当我们看一个截图时,理解更加清晰,如下:
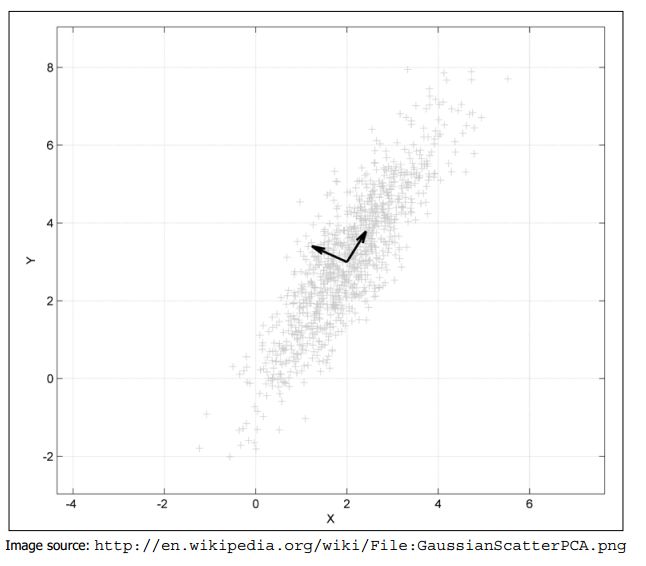
先前的截图展示了一个中心在(2,3)的多元高斯分布的PCA。所示的向量是协方差矩阵的特征向量。移动向量,这样它们的尾巴在均值处。
如果我们想用一个单一的参数表示我们的模型,那么将这些点的特征矢量的方向转移到截图的右上部分将是一个好的方法。而且,通过轻微的改变参数,我们可以推断数据并且获得类似于我们将要寻找的值。
浅尝PCA——Getting the feel of PCA
为了获得PCA是怎么样帮助我们人脸模型的一个感觉,我们将开始一个主动形状模型并且测试一些参数。
因为人脸检测和跟踪已经学习了一段时间,对于研究的目标,几个人脸数据库可以在线访问到。我们将使用来至于IMM数据集的一对样本。
首先,让我们理解一些OpenCV中PCA类是怎么工作的。我们可以从文献中得到结论:PCA类用来计算一组矢量的特殊基,它包含通过一组输入矢量计算得到协方差矩阵的特征矢量。这个类同样可以使用project 和backproject方法将矢量投影到新的坐标空间或者从新的坐标空间反投影到原空间,仅通过获取它的前几个少量成分就可以精确的估计这个新的坐标系统。这意味着我们可以使用一个非常短的子空间中的投影矢量坐标组成的矢量来表示来至高维空间的原始矢量。
因为在少量尺度值方面,我们将要一个参数化,我们将要使用的主要方法来至于类的backproject方法。它带有投影矢量的主成份坐标并且重构这些原始坐标。如果我们保留所有的成分,我们可以重新获得原始矢量,但是如果我们仅使用两个成分,差别将非常小。这是使用PCA的一个理由。既然我们想得到围绕原矢量的变换,我们参数化尺度将能够推断原始数据。
而且,通过基的定义,PCA类可以转换矢量到新的坐标空间和从新的坐标空间反投影到原空间。从数学上讲,它意味着我们计算矢量的投影到一个子空间,该子空间是通过与协方差矩阵的主导特征值相对应的一些少量的特征矢量形成,就像我们从文献中看到的那样。
我们将用landmark标记一下我们的人脸图像来为点分布模型(point distribution model PDM)产生一个训练集。如果我们有k个二维的对齐标记,我们的形状可以描述为:
X = { x1, y1, x2, y2, …, xk, yk}
我们需要所有图像上的一致性的标记,这很重要。因此,例如,如果第一个图像上嘴的左边部分的是标记3,这将需要所有的其他图像上的也是标记3.
现在这些标记序列将形成形状的轮廓,并且一个给出的训练形状可以定位为一个矢量。一般地我们假定这些分布是在这个空间上的高斯分布,并且我们使用PCA来计算所有训练形状形成的协方差矩阵的标准化特征矢量和特征值。使用中上的特征矢量,我们创建一个2k*m的矩阵,我们称它为P。这样,每个特征矢量描述为这个集合变化的一个主要模式。
现在我们可以通过下面的等式定义一个新的形状:
X' = X' + Pb
这里,X’是所有训练图像的均值形状——我们刚刚计算的标记的每一个平均——以及b是一个尺度化每一个主成份的矢量。这引导我们通过修改b的值创建一个新的形状。
通常将b设置在3个标准差范围内,这样产生的形状可以落入训练集。
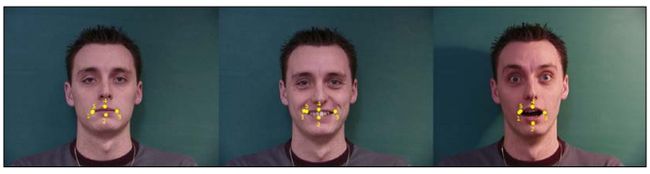
下面的截图展示了用点注释的嘴标记的3个不同图像:
就像我们在先前截图看到的那样,形状通过它们的标记序列来描述。我们可以使用一个像GIMP或者ImageJ的程序,同样地在OpenCV中建立一个简单的应用,为了标记这些训练图像,我们将假定用户已经完成了这个过程并且为所有的训练图像将这些点保存为x和y标记位置的序列,存储到一个文本文件中,这在我们的PCA分析中将有用。然而,我们将添加两个参数到这个文件的第一个行,即训练图像的数目和读取列的数目。因此,对于K个2D点,这个数字是2*k。
在下面的数据中,我们有一个这个文件的一个例子,我们通过对IMMdatabase中的三个图像的标记获得。这里k是5:
3 10
265 311 303 321 337 310 302 298 265 311
255 315 305 337 346 316 305 309 255 315
262 316 303 342 332 315 298 299 262 316
既然我们已经标记了图像,让我们将这些数据带入我们的形状模型。首先,导入这些数据到一个矩阵。这个过程通过函数loadPCA来完成。下面的代码片段展示了loadPCA函数的使用。
PCA loadPCA(char* fileName, int& rows, int& cols,Mat& pcaset){ FILE* in = fopen(fileName,"r"); int a; fscanf(in,"%d%d",&rows,&cols); pcaset = Mat::eye(rows,cols,CV_64F); int i,j; for(i=0;i<rows;i++){ for(j=0;j<cols;j++){ fscanf(in,"%d",&a); pcaset.at<double>(i,j) = a; } } PCA pca(pcaset, // pass the data Mat(), // we do not have a pre-computed mean vector, // so let the PCA engine compute it CV_PCA_DATA_AS_ROW, // indicate that the vectors // are stored as matrix rows // (use CV_PCA_DATA_AS_COL if the vectors are // the matrix columns) pcaset.cols// specify, how many principal components to retain ); return pca; }注意我们的矩阵在pcaset=Mat::eye(rows,cols,CV_64F)中创建并且有足够的容量来存储2*k个值。两个for循环导入数据到这个矩阵后,调用带有一个数据和一个空矩阵的PCA构造器,如果我们希望仅使用它一次,那么这个矩阵是空矩阵,当然也可以是我们预先计算的均值矢量。我们同样指出我们的矢量将作为矩阵的行存储并且我们希望保持给定行(这里应该是列)的数目和成分数目相同,尽管我们可能仅使用少量的成分。
既然我们用我们的训练集填充了我们的PCA对象,根据给定的参数,它拥有所需的所有事情来反投影我们的形状。我们通过调用PCA.backproject来这样做,传递参数作为一个行矢量并且在第二个参数中获得反投影矢量。
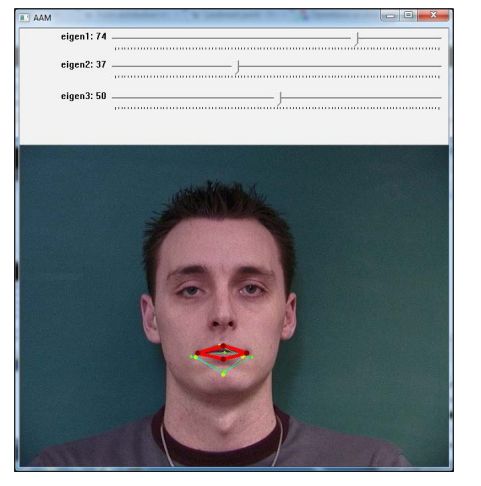
先前的两个截图展示了根据滑动滚动条选择的两个不同形状的配置参数。黄色和绿色形状表明训练数据集,红色形状反映了选择参数产生的形状。
一个简单的应用程序可以用来做主动形状模型实验,对于模型,它允许用户尝试不同的参数。我们能够注意到通过滑动滑块(分别对应于第一个和第二个变化模式),仅前两个尺度值发生变化,我们可以获得一个形状,这个形状可以非常接近于训练的形状。当我们在AAM中搜索一个模型时,这样的可变性将帮助我们。因为它提供了插值形状。我们将在接下来的部分讨论三角剖分,纹理,AAM和AAM-search。
因为我们正在寻找的形状可能被歪曲,例如张开嘴的一个实例,我们需要将我们的纹理映射到一个均值形状,然后对这个标准化的纹理应用PCA。为了这样做,我们将使用三角剖分。它的概念非常简单:我们创建三角形包含我们标记的点,然而从一个三角形映射到另外一个三角形。OpenCV带有一个标记的函数,叫做cvCreateSubdivDelaunay2D,它创建一个空的Delaunay三角剖分。你可以仅认为这是一个好的三角剖分,它可以避免瘦长三角形。
在数学和计算几何上,平面内一个点集P的Delaunay三角剖分是一个这样的一个三角剖分:P中的每一个点都不会落在任何三角形的外接圆内。在三角剖分中,Delaunay三角剖分最大化三角形中所有角的最小角。从1934年之后,三角剖分以Boris Delaunay在这个方面的工作而命名。
一个Delaunay划分初始化之后,我们将使用cvSubdivDelaunay2DInsert函数将这些点填充到三角划分中。下面的代码行将说明一个三角剖分的直接使用将是什么样的:
CvMemStorage* storage; CvSubdiv2D* subdiv; CvRect rect = { 0, 0, 640, 480 }; storage = cvCreateMemStorage(0); subdiv = cvCreateSubdivDelaunay2D(rect,storage); std::vector<CvPoint> points; //initialize points somehow ... //iterate through points inserting them in the subdivision for(int i=0;i<points.size();i++){ float x = points.at(i).x; float y = points.at(i).y; CvPoint2D32f floatingPoint = cvPoint2D32f(x, y); cvSubdivDelaunay2DInsert( subdiv, floatingPoint ); }
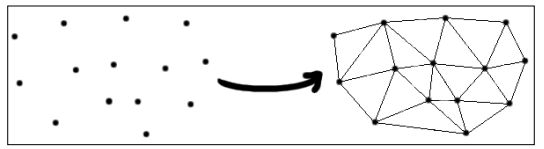
注意我们的点都是在一个矩形框架内,这个矩形将作为一个参数传递给cvCreateSubdivDelaunay2D。为了创建一个划分,我们也需要创建和初始化一个内存存储器。这可以在先前的代码的前5行看到。然而,为了创建三角剖分,我们需要使用cvSubdivDelaunay2DInset函数插入这些点。这发生在先前代码的for循环中。请注意点应当已经被初始化,因为它们是我们正在使用作为输入的点。下面的截图展示了三角剖分可能是什么样子:
这个截图是针对一组点先前的代码的输出,是使用Delaunay算法产生的三角剖分。
尽管划分的创建是OpenCV的一个非常便利的函数,迭代遍历所有的三角剖分可能不是非常简单。下面的代码展示了如何迭代遍历一个子划分的边。
void iterate(CvSubdiv2D* subdiv, CvNextEdgeType triangleDirection){ CvSeqReader reader; CvPoint buf[3]; int i, j, total = subdiv->edges->total; int elem_size = subdiv->edges->elem_size; cvStartReadSeq((CvSeq*)(subdiv->edges), &reader, 0); for(i = 0; i < total; i++){ CvQuadEdge2D* edge = (CvQuadEdge2D*)(reader.ptr); if(CV_IS_SET_ELEM(edge)){ CvSubdiv2DEdge t = (CvSubdiv2DEdge)edge; for(j=0;j<3;j++){ CvSubdiv2DPoint* pt = cvSubdiv2DEdgeOrg(t); if(!pt) break; buf[j] = cvPoint(cvRound(pt->pt.x), cvRound(pt->pt.y)); t = cvSubdiv2DGetEdge(t, triangleDirection); } } CV_NEXT_SEQ_ELEM(elem_size, reader); } }给定一个剖分,我们初始化它的边读器(edge reader)称为cvStartReadSeq函数。从OpenCV的文献中,我们引用如下的定义:
函数初始化reader的状态,然后,所有序列元素,从第一个到最后一个,在前向阅读的情况下,可以通过调用子序列的宏CV_READ_SEQ_ELEM,在反向阅读的情况下,调用宏CV_REV_READ_SEQ_ELEM.。这两个宏将序列元素放入到read_elem并且移动reading 指针指向下一个元素。
获得接下来的元素的一个可替代的方式是使用宏CV_NEXT_SEQ_ELEM(elem_size,reader),如何序列元素很多,它是首选的。在这种情况下,我们使用CvQuadEdge2D *edge=(CvQuadEge2D*)(reader.ptr)来访问边缘,这仅是一个从一个reader指针到CvQuadEdge2D指针的一个强制转换。宏CV_IS_SET_ELEM仅检查指定的边是否被占用。给定一个边,我们需要调用cvSubdiv2DEdgeOrg函数来获得该边的源点。为了遍历一个三角形,我们重复的调用cvSubdiv2DEdge并且传递三角形方向,例如它可以是AROUND_LEFT或者CV_NEXT_AROUND_RIGHT.
三角纹理变形(映射)——Triangle texture warping
既然我们能够 迭代的访问一个划分的三角形,我们能够将一个原始标记的图像变换到一个产生的扭曲的图像。这对于将原始形状的纹理映射到扭曲的形状很有用。下面的代码将引导这个过程:
void warpTextureFromTriangle(Point2f srcTri[3], Mat originalImage, Point2f dstTri[3], Mat warp_final){ Mat warp_mat(2, 3, CV_32FC1); Mat warp_dst, warp_mask; CvPoint trianglePoints[3]; trianglePoints[0] = dstTri[0]; trianglePoints[1] = dstTri[1]; trianglePoints[2] = dstTri[2]; warp_dst = Mat::zeros(originalImage.rows, originalImage.cols, originalImage.type()); warp_mask = Mat::zeros(originalImage.rows, originalImage.cols, originalImage.type()); /// Get the Affine Transform warp_mat = getAffineTransform(srcTri, dstTri); /// Apply the Affine Transform to the src image warpAffine(originalImage, warp_dst, warp_mat, warp_dst.size()); cvFillConvexPoly(new IplImage(warp_mask), trianglePoints, 3, CV_ RGB(255,255,255), CV_AA, 0); warp_dst.copyTo(warp_final, warp_mask); }先前的代码假定我们有了三角形顶点,并且存储 在srcTri数组中以及目的点存储在dstTri数组中。2×3的warp_mat矩阵用来获取从源三角形到目的三角形的仿射变换。更多的信息可以OpenCV的cvGetAffineTransform文献中引用。
函数cvGetAffineTransform计算一个仿射变换的矩阵,如下:
在前面的等式中,目的(i)
获得仿射矩阵之后,我们可以应用仿射变换到源图像。这通过warpAffine函数实现。因为我们不像在整个图像上进行——我们想关注我们的三角形——掩码可以用来完成这个任务。这样,最后一行代码仅拷贝带有刚才创建的掩码的源图像上的三角形,掩码通过函数cvFillConvexPoly调用填充。
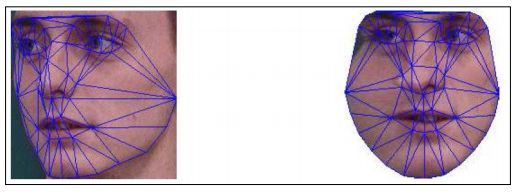
下面的截图展示了应用这个过程到注释图像中的每一个三角形的结果。注意这些三角形映射到匹配的框架,他们的脸朝向视者。这个过程用于创建AAM的统计纹理。
前面的截图展示了将左图像中所有的三角形映射到了一个平均参考框架。
模型实例化——使用主动表观模型——Model Instantiation-playing with the Active Appearance Model
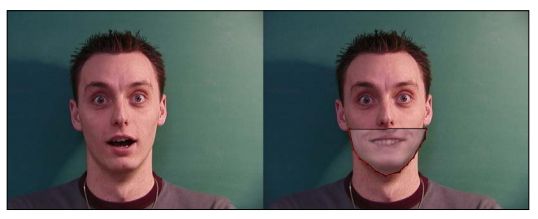
AAM有趣的一面是它们能够简单地插值我们训练图像的模型。通过一对形状或者模型参数的调整,我们可以习惯于他们表现出的惊人的力量。当我们改变形状参数时,根据训练形状数据我们的变化方向发生了变化。另一方面,当表观参数修改时,基于形状的纹理也发生修改。我们的扭曲变换将每一个三角形从基本形状变换到修改的目的形状,因为我们可以在一个张开的嘴上组合一个关闭的嘴,将像下面截图展示的那样:
前面的截图展示了一个组合的闭合嘴,它是通过另外一个图像上的主动表观形状的实例化获得的。它表明我们是怎样组合一个微笑的嘴和一个钦佩的脸,推断训练的图像。
前面的截图是通过仅改变形状的三个参数和纹理的3个参数获得的,这是AAM的目标。对于想使用AAM的读者,一个简单的应用的开发可以在访问的到。实例化一个模型仅是简单的滑动等式参数的问题,就像Getting the feel of PCA部分定义的那样。你应当注意AAM搜索和匹配依赖这种灵活性为给定的模型捕获到帧找到最佳匹配,我们的模型的来至于训练集中的不同位置。我们将在接下来的部分看到。
AAM搜索和匹配——AAM search and fitting
带着新的组合的形状和纹理,我们发现了一个很好的方式来描述人脸不仅在形状上而且在表观上是怎样变化的。现在我们想找一组p形状参数和lambda个表观参数,能将我们的模型尽可能的接近于一个给定的输入图像I(x)。自然地,我们可以在I(x)的坐标框架内计算我们的实例化模型和给定输入图像之间的误差,或者将这些点投影到基本表观并且计算那里的差异。我们将使用后面的这个方法。这样,我们想最小化下面的函数:
在上面的等式中,S0表示像素集x等于(x,y)T,(x,y)T位于AAM基本网格的内部。A0x是我们基本网格的纹理。Ai(x)是来至PCA的表观图像,W(x:p)是像素从输入图像投影到基本网格框架的变换。
通过多年的研究,提出了几个能够实现这个最小化的方法。第一个思想是使用一个增加的方法,其中 ∆pi和∆λi作为误差图像的线性函数来计算。然后,形状参数p和表观λ在第i次迭代中作为 pi← pi+ ∆pi和 λi← λi+ ∆λi来更新。尽管收敛有时发生,delta不总是依赖于当前的参数,并且这可能导致发散。另外一个方法非常慢,它是基于梯度下降法的研究,因此寻找另外一个收敛的方法被找到。替代更新参数,可以更新整体变换。这样,Ian Mathews 和Simon Baker在他们著名的论文称为:再去访问主动表观模型(Active Appeance Models Revisited)中提出。更多的细节可以在这篇论文中找到,它给匹配的一个重要的贡献是它将大部分的密集型计算带到了预计算步骤,就像下面的截图所看到的那样:
注意更新发生在组合步骤(9)(看上面的截图)。等式(40)和(41)来至论文,可以在下面的截图看到:
尽管算法仅提到从一个位置靠近最后一个位置大部分收敛的很好。当在旋转、平移和尺度上存在一个大的差异时,这可能不适应于这样的情况。我们可以通过一个全局的2D相似变换的参数化将更多的信息带到收敛。这是论文中的等式42,展示如下:
在上面的等式中,这四个参数q=(a,b,tx,ty)T有下面的阐述。第一对(a,b)与尺度k和旋转θ相关,a等于kcos(theta)-1,b=ksin(theta)。第二对(tx,ty)是x,y上的平移。就像在再次访问主动形状模型文章中提到的那样。
带有更多的数学变换,最终我们可以使用前面的算法来找到和一个全局2D变换最匹配的图像。
因为变形(warp)组合算法有几个性能优点,我们将使用在AAM Revisited论文中描述的那个,反向组合投影算法(inverse compositional project-out algorithm)。记住在这个方法中,匹配时表观的效果可以预先处理,或者投射出——提升AAM匹配性能。
下面的截图展示了使用反向组合投射AAM匹配算法得到的来至MUCT数据库不同图像的收敛:
先前的截图现实了成功的收敛——脸的外部AAM训练集——使用了inverse compositional project-out AAM fitting algorithm。
POSIT——姿态
我们找到我们标记点的2D位置之后,我们可以使用POSIT获得我们模型的3D姿态。一个3D对象的姿态P定义为3×3的旋转矩阵R和3D平移向量T,因此P等于[R|T]。
注释:
这节大部分是基于Javier Barandiaran编写的OpenCV POSIT手册。
像名字暗示的那样,在若干次迭代中,POSTI使用“姿态来至于正交和尺度”算法,因此,它是POS和迭代的缩写。它假设我们可以在图像中检测和匹配四个或者更多的目标的非共面特征点并且我们知道这个目标上的相关几何。
该算法的主要思想是我们可以找到一个关于目标姿态的好的近,这假定所有模型点在同一个平面内。因为如果我们比较相机到一个人脸的距离,这些点的深度将非常不同。初始化姿态获得之后,通过解决一个线性系统找到目标的旋转矩阵和平移向量。然而,近似的估计迭代地用来更好地计算特征点的尺度化正交投影,跟随着这些投影(而不是原始点)的POS应用。为了获得更多的信息,我们可以参考: the paper by DeMenton, Model-Based Object Pose in 25 Lines of Code.
投入到POSIT——Diving into POSIT
为了使POSIT工作,我们至少需要4个非共面模型3D点和它们各自的2D图像中的匹配。我们增加一个结束标准,因为POSIT是一个迭代算法——一般地它是迭代的次数或者一个距离参数。然后,我们调用cvPOSIT函数,这个函数产生旋转矩阵和平移矢量。
作为一个例子,我们将跟随着JavierBrandianran编写的手册,它用POSIT来获得一个立方体的姿态。模型用4个点创建。用下面的代码初始化:
float cubeSize = 10.0; std::vector<CvPoint3D32f> modelPoints; modelPoints.push_back(cvPoint3D32f(0.0f, 0.0f, 0.0f)); modelPoints.push_back(cvPoint3D32f(0.0f, 0.0f, cubeSize)); modelPoints.push_back(cvPoint3D32f(cubeSize, 0.0f, 0.0f)); modelPoints.push_back(cvPoint3D32f(0.0f, cubeSize, 0.0f)); CvPOSITObject *positObject = cvCreatePOSITObject( &modelPoints[0], static_cast<int>(modelPoints.size()) );
注意模型本身用cvCreatePOSITObject方法创建,它返回一个将在cvPOSIT函数中使用的一个CvPOSITObject方法。注意,姿态将参考第一个模型点来计算,这使得将它放在原点是个好的主意。
然而,我们需要将2D图像点放入到另外一个vector中。记住,这些点必须以同样的顺序放置在数组中,模型的点插入到这个数组中。这样,第i个2D图像点匹配第i个3D模型点。这里,一个问题是2D图像点的原点位于图像的中心,这可能需要你平移它们。你可以插入下面的2D图像点(当然,它们将根据用户的匹配变化)。
std::vector<CvPoint2D32f> srcImagePoints; srcImagePoints.push_back( cvPoint2D32f( -48, -224 ) ); srcImagePoints.push_back( cvPoint2D32f( -287, -174 ) ); srcImagePoints.push_back( cvPoint2D32f( 132, -153 ) ); srcImagePoints.push_back( cvPoint2D32f( -52, 149 ) );
现在,你仅需要为矩阵分配内存和创建终止标准,接着调用cvPOSIT,就像下面的代码片段展示的那样:
//Estimate the pose CvMatr32f rotation_matrix = new float[9]; CvVect32f translation_vector = new float[3]; CvTermCriteria criteria = cvTermCriteria(CV_TERMCRIT_EPS | CV_ TERMCRIT_ITER, 100, 1.0e-4f); cvPOSIT( positObject, &srcImagePoints[0], FOCAL_LENGTH, criteria, rotation_matrix, translation_vector );迭代完成之后,cvPOSIT将结果存储在rotation_matrix和translation_vector.下面的截图展示了带有白色圆圈的scrImgePoints,以及一个坐标轴来表明旋转和平移的结果。
参考前面的截图,让我们看一下输入的点和运行POSIT算法的结果:
1、白色圆圈表示输入点,同时坐标轴表示结果模型的姿态。
2、当通过一般标定过程获得焦距时,请确保你的相机使用了焦距。你可能想检查一下标定的过程可以访问:in the Camera calibrationsection in Chapter 2, Markerbased Augmented Reality on iPhone or iPad. POSIT当前的实现仅允许正方形的像素,因为对于焦距的长度没有余地在x和y轴上。
3、期望的旋转矩阵为下面的格式:
4、平移矢量为下面的格式:
为了使用POSIT作为姿态估计的一个工具,我们将使用一个3D头部模型。
There is one available from the Institute of Systems and Robotics of the University of Coimbra and can be found at
注意这个模型可以在它描述的地方获得:
float Model3D[58][3]= {{-7.308957,0.913869,0.000000}, ...
这个模型可以通过下面的截图看到:
先前的截图展示了POSIT可利用的一个58个点的3D头部模型。
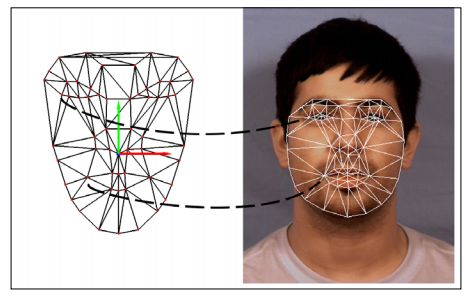
为了使POSIT工作,相对于3D头部模型的点必须相应地匹配。注意,至少需要4个非共面的点和它们相应的2D投影来使POSIT工作,因此,它们必须作为参数传递,大致上和Diving into POSIT部分描述的那样。注意这个算法在匹配点的数量方面是线性的。下面的截图展示了匹配是怎么样完成的:
先前的截图展示了一个3D头部模型和一个AAM网格的正确的匹配点。
从网络摄像机或者视频文件跟踪——Tracking from webcam or video file
既然我们已经收集了所有的工具来获得6个自由度的人脸跟踪。我们可以应用它到一个相机流或者视频文件。OpenCV提供了VideoCapture类,这个类可以用下面的方式使用(获取跟到的信息,可以看:see the Accessing the webcamsection in Chapter 1, Cartoonifier and Skin Changer for Android)
#include "cv.h" #include "highgui.h" using namespace cv; int main(int, char**) { VideoCapture cap(0);// opens the default camera, could use a // video file path instead if(!cap.isOpened()) // check if we succeeded return -1; AAM aam = loadPreviouslyTrainedAAM(); HeadModel headModel = load3DHeadModel(); Mapping mapping = mapAAMLandmarksToHeadModel(); Pose2D pose = detectFacePosition(); while(1) { Mat frame; cap >> frame; // get a new frame from camera Pose2D new2DPose = performAAMSearch(pose, aam); Pose3D new3DPose = applyPOSIT(new2DPose, headModel, mapping); if(waitKey(30) >= 0) break; } // the camera will be deinitialized automatically in VideoCapture // destructor return 0; }算法是这样运作的。一个视频捕捉通过VideoCapture(0)来初始化,因此将使用默认的相机。既然我们使得视频捕捉工作了,同样地我们需要我们训练的主动表观模型,这在伪代码load PreviouslyTrainedAAM mapping中实现。我们同样为POIST算法导入3D头部模型并且导入存储在映射变量中的标记点到3D头部点的映射。
我们需要的所有事情导入之后,我们将从一个已知的姿态初始化算法,这是一个已知的3D姿态,已知的旋转和已知的一组AAM参数。这将通过OpenCV详细记载的Haar特征分类人脸检测器自动的完成(更多的细节在第六章非刚性人脸跟踪中的人脸检测器部分,或者OpenCV的级联分类器文献),或者我们可能手动地从先前标记的框架中初始化一个姿态。
同样可以使用一个brute-force方法,它将为每一个矩形运行一个AAM匹配,因为仅在第一帧的搜索中它很慢。注意通过初始化,我们想要通过它们的参数找到AAM的2D标记。
当所有的事情导入了之后,我们可以通过while 循环限定的主循环来进行迭代。在这个循环中,我们首先访问下一个获取的视频帧,然后我们运行一个主动表观模型,以便我们可以在下一帧图像中找到标记。既然在这一步,当前位置非常重要,我们将它作为一个参数传递给伪代码函数performAASearch(pose,aam)。如果我们找到了当前姿态,它通过误差图像收敛传递了一个信号,我们将获取下一个标记位置,因此我们可以将它们提供给POSIT。这发生在下面的命令行:applyPOSIT(new2DPose,headModel,mapping),这里新的2D姿态作为一个参数传递,同样地像我们先前导入的headModel和mapping。之后,我们可以在获得姿态中渲染任何3D模型,如一个坐标系轴或者一个增强现实的模型。当我们有了标记,通过模型的参数化可以获得更多有趣的效果,例如张开嘴或者改变眉毛的位置。
总结——Summary
在这一章,我们已经讨论了主动表观模型是怎么样和POSIT组合来获得一个3D头部姿态。关于如何创建,训练和操作AAM的概述已经给出,读者可以使用这些背景到任何领域,例如医疗,图像处理,或者企业。进一步处理AAMs,我们熟悉了Delaunay三角剖分并且学习了如何使用这样有趣的结构作为一个三角剖分的网格。我们同样展示了如何OpenCV函数在三角形上执行纹理映射。另外一个感兴趣的主题是AMM匹配的方法。尽管只描述了反向组合投影算法,我们可以简单的通过使用它的输出来获得多年研究的结果。
学习了充足的理论和AAM的实践之后,我们投入到POSIT的细节来结合2D测量到3D测量,来阐述如何使用两个模型点之间的匹配来适配(拟合)一个3D模型。我们通过展示如何使用所有的工作到一个在线的人脸跟踪,这产生了6个自由度的头部姿态——个3的旋转度——3个平移。本章完整的代码可以从下载。
参考——References
• Active Appearance Models, T.F. Cootes, G. J. Edwards, and C. J. Taylor, ECCV,
2:484–498, 1998(~efros/courses/AP06/Papers/
cootes-eccv-98.pdf)
• Active Shape Models – Their Training and Application, T.F. Cootes, C.J. Taylor,
D.H. Cooper, and J. Graham, Computer Vision and Image Understanding, (61):
38–59, 1995(~bim/Papers/cviu95.pdf)
• The MUCT Landmarked Face Database, S. Milborrow, J. Morkel, and F. Nicolls,
Pattern Recognition Association of South Africa, 2010(
muct/)
• The IMM Face Database – An Annotated Dataset of 240 Face Images, Michael M.
Nordstrom, Mads Larsen, Janusz Sierakowski, and Mikkel B. Stegmann,
Informatics and Mathematical Modeling, Technical University of Denmark, 2004,
(~aam/datasets/datasets.html)
• Sur la sphère vide, B. Delaunay, Izvestia Akademii Nauk SSSR, Otdelenie
Matematicheskikh i Estestvennykh Nauk, 7:793–800, 1934
• Active Appearance Models for Facial Expression Recognition and Monocular Head
Pose Estimation Master Thesis, P. Martins, 2008
• Active Appearance Models Revisited, International Journal of Computer Vision,
Vol. 60, No. 2, pp. 135 - 164, I. Mathews and S. Baker, November, 2004
(
matthews_iain_2004_2.pdf)
• POSIT Tutorial, Javier Barandiaran(
wiki/Posit)
• Model-Based Object Pose in 25 Lines of Code, International Journal of Computer
Vision, 15, pp. 123-141, Dementhon and L.S Davis, 1995(
umd.edu/~daniel/daniel_papersfordownload/Pose25Lines.pdf)
书中章节如下:
1、卡通化和肤色改变 for Androd
2、基于标记增强现实 On iPhone
3、无标记增强现实
4、利用OpenCV探测来至运动的结构
5、采用SVM和神经网络的车牌识别
6、非刚性人脸跟踪
7、采用AAM的3D姿态估计和POSIT
8、采用主成分分析和线性判别分析的人脸识别