《数据结构与算法分析》AVLTree详解
前言:
上一篇博客讲完了最基础的二叉查找树,现在总算进入到第一个难题了,AVLTree。实话说这一颗树的实现花费了我整整一天的时间,编码半天,调试正确又花了半天。在自己不断的调试,检查之后,总算是完美的实现了。这一颗树书上只给出了插入操作,我根据AVLTree 的要求自行想出了删除操作的方法,并且成功实现了,让我觉得对于数据结构,我总算是成功入门了吧。
我的github:
我实现的代码全部贴在我的github中,欢迎大家去参观。
https://github.com/YinWenAtBIT
介绍:
定义:
AVL树实际上就是保持了左右子树相对平衡的二叉查找树。它保证每一个节点的左右子树都满足一个平衡条件:即左右子树的高度差小于2。
AVL树以其发明者前苏联学者G.M. Adelson-Velsky 和 E.M. Landis 名字而命名,他们在1962年的论文《An algorithm for the organization of information》中发表了它。
旋转:
AVLTree中最关键的地方就是:如果插入或者删除了节点,导致左右高度差距大于等于2,那么如果保持平衡?对于这个问题有4种情况,分别求解:
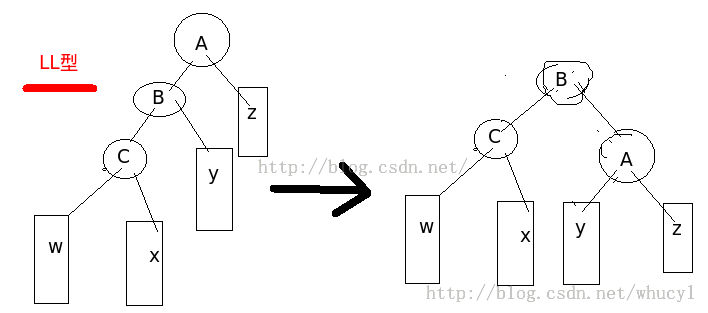
左左/右右情况:
如下图所示为左左的情况,即A的左子树高于右子树2,并且其左子树也满足左子树比右子树高。右右情况同理。这时需要进行一次右旋转,使得B成为新的根节点。A变成B的右子树,且B的右子树变成A的左子树。这样的旋转叫做一次单旋转。
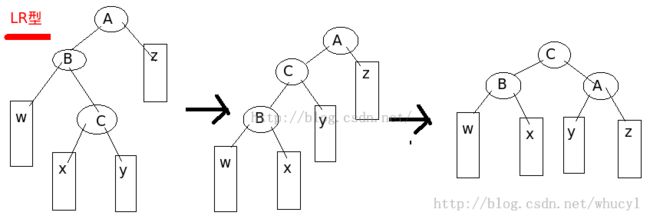
左右/右左情况:
如下图所示为左右的情况,即A的左子树高于右子树2,但是其左子树满足其左子树比右子树低。右左情况同理。这时如果进行一次如上图所示的右旋转,将导致B的右子树高于左子树(大家可以自行画图尝试一下),那么这时就需要进行一次双旋转。
先对A的左子树B进行一次左旋转。这将导致A的左子树变成C(右右情况的旋转),此时已经变回了左左的图形了,那么再进行一次右旋转即可。右左型的操作相似,相信大家肯定可以推出来。
树结构:
因为要保持左右子树的高度平衡,所以在每个节点中必须要保存高度信息
struct AVLNode
{
ElementType Element;
AVLTree Lchild;
AVLTree Rchild;
int Hight;
};
操作:
高度:
高度信息是第一个需要定义的,因为之后所有的删除插入操作都与之有关,定义一个节点没有子树,那么他的高度是0,往上依次递增。一个节点的高度等于他左右子树的高度的最大值加1。因此,定义NULL指针的高度为-1,叶子节点的高度同样为左右子树高度最大值加1。
/*返回树节点的高度,如果为NULL返回-1*/
int Hight(AVLTree T)
{
if(T == NULL)
{
return -1;
}
return T->Hight;
}
右旋转:
该节点的左孩子高度上升,它变为左孩子的右子树,左节点的右子树变成它的左节点。说起来有点绕口,大家看代码应该就明白了。
AVLTree RightSingleRotate(AVLTree T)
{
AVLTree k1;
k1 = T->Lchild;
T->Lchild = k1->Rchild;
k1->Rchild = T;
T->Hight = Max(Hight(T->Lchild), Hight(T->Rchild)) +1;
k1->Hight = Max(Hight(k1->Lchild), Hight(k1->Rchild)) +1;
return k1;
}
左旋转:
左旋转的操作与右旋转操作对称。
AVLTree LeftSingleRotate(AVLTree k1)
{
Position k2;
k2 = k1->Rchild;
k1->Rchild = k2->Lchild;
k2->Lchild = k1;
k1->Hight = Max(Hight(k1->Lchild), Hight(k1->Rchild))+1;
k2->Hight = Max(Hight(k2->Lchild), Hight(k2->Rchild))+1;
return k2;
}
双旋转:
双旋转为左右旋转或者右左旋转,调用之前定义好的左右旋转代码即可。
AVLTree RightDoubleRotate(AVLTree k3)
{
k3->Lchild = LeftSingleRotate(k3->Lchild);
return RightSingleRotate(k3);
}
/*右边树枝双旋转*/
AVLTree LeftDoubleRotate(AVLTree k1)
{
k1->Rchild = RightSingleRotate(k1->Rchild);
return LeftSingleRotate(k1);
}
插入:
在这里我使用递归的方式插入,实现的方式与上一节的二叉查找树相同,唯一的区别就是在执行了插入操作之后需要检查左右子树的高度是否平衡,不平衡就需要根据节点情况调用单旋转或者双旋转。并且在最后更新该节点的高度,以便其父节点用来更新高度信息。
AVLTree Insert(ElementType X, AVLTree T)
{
if(T == NULL)
{
T = (AVLTree)malloc(sizeof(AVLNode));
if(T ==NULL)
exit(1);
T->Element = X;
T->Lchild = T->Rchild = NULL;
T->Hight = 0;
}
if(X <T->Element)
{
T->Lchild = Insert(X, T->Lchild);
/*左边插入之后检查是否满足平衡条件,如果不平衡需要进行旋转*/
if( (Hight(T->Lchild)-Hight(T->Rchild)) == 2)
{
if(X< T->Lchild->Element)
T = SingleRotateLeft(T);
else
T = DoubleRotateLeft(T);
}
}
if(X >T->Element)
{
T->Rchild = Insert(X, T->Rchild);
/*右边插入之后检查是否满足平衡条件,如果不平衡需要进行旋转*/
if((Hight(T->Rchild) - Hight(T->Lchild)) ==2)
{
if(X >T->Rchild->Element)
T = SingleRotateRight(T);
else
T = DoubleRotateRight(T);
}
}
/*X in the Tree already, we will do nothing*/
/*插入完成更新该节点高度*/
T->Hight = Max(Hight(T->Lchild), Hight(T->Rchild)) +1;
return T;
}
删除:
删除的方式与二叉查找树树也相同,我在这里实现的方式同样是递归删除。与插入一样,删除之后需要检查左右节点的高度是否还平衡,不平衡就调用旋转,最后再更新自己的高度信息。
/*递归删除*/
AVLTree Delete(ElementType X, AVLTree T)
{
if(T == NULL)
{
fprintf(stderr, "%d not exist\n", X);
}
else
{
if(X < T->Element)
{
T->Lchild = Delete(X, T->Lchild);
/*删除之后需要更新该节点高度*/
T->Hight =Max(Hight(T->Lchild), Hight(T->Rchild))+1;
/*删除之后检查是否满足平衡条件,不满足需要旋转*/
if((Hight(T->Rchild) - Hight(T->Lchild)) == 2)
{
if(Hight(T->Rchild->Rchild) >= Hight(T->Rchild->Lchild))
T = SingleRotateRight(T);
else
T = DoubleRotateRight(T);
}
}
else if(X > T->Element)
{
T->Rchild = Delete(X, T->Rchild);
/*删除之后需要更新该节点高度*/
T->Hight =Max(Hight(T->Lchild), Hight(T->Rchild))+1;
/*删除之后检查是否满足平衡条件,不满足需要旋转*/
if((Hight(T->Lchild) - Hight(T->Rchild)) == 2)
{
if(Hight(T->Lchild->Lchild) >= Hight(T->Lchild->Rchild))
T = SingleRotateLeft(T);
else
T = DoubleRotateLeft(T);
}
}
else
{
/*找到的树节点如果有两个孩子的话就用它右子树的最大值代替该点,再删去右子数上的最大值*/
if(T ->Lchild &&T->Rchild)
{
T->Element = FindMin(T->Rchild)->Element;
T->Rchild = Delete(T->Element, T->Rchild);
T->Hight =Max(Hight(T->Lchild), Hight(T->Rchild))+1;
if((Hight(T->Lchild) - Hight(T->Rchild)) == 2)
{
if(Hight(T->Lchild->Lchild) >= Hight(T->Lchild->Rchild))
T = SingleRotateLeft(T);
else
T = DoubleRotateLeft(T);
}
}
else
{
AVLTree temp = T;
if(T->Lchild == NULL)
T= T->Rchild;
else
T= T->Lchild;
free(temp);
}
}
}
return T;
}
总结:
在自行实现删除操作的时候,最初遇上了非常多的对NULL节点进行访问的操作,问题出在自己考虑问题还不够周全。解决的方式就是跟着代码一步步的调试,发现在哪一步上对NULL指针进行了访问,然后修复这个问题。更新高度最初也没有实现,删除之后树就畸形了,也是自己思考之后尝试添加了更新高度的代码,然后成功了。自己实现了删除操作让我备受鼓舞,毕竟以前总是在逃避这些问题,当我自己直面时,发现这些问题也不过如此。按照自己的思路去实现,出了问题慢慢调试,原来一些都这么简单。