基于连通图的分裂聚类算法
参考文献:基于连通图动态分裂的聚类算法.作者:邓健爽 郑启伦 彭宏 邓维维(华南理工大学计算机科学与工程学院,广东广州510640)
我的算法库:https://github.com/linyiqun/lyq-algorithms-lib
算法介绍
从文章的标题可以看出,今天我所介绍的算法又是一个聚类算法,不过他比较特殊,用到了图方面的知识,而且是一种动态的算法,与BIRCH算法一样,他也是一种层次聚类的算法,BIRCH算法是属于那种,一步步慢慢合并从而形成最终的聚类结果,而本文所描述的算法则恰巧相反,通过不断分裂直到最后不能在分裂下去为止,事实上,通过分裂实现的聚类的算法并不常见,平时说的比较多的这种算法就是chameleon算法,基于连通图的分裂聚类算法与此很类似,但又有少许的不同。首先声明这个算法的提出是出自于某篇学术论文,人家提出了这个思想,我去做了一下学习和实现,所以在这里分享一下。
算法的原理
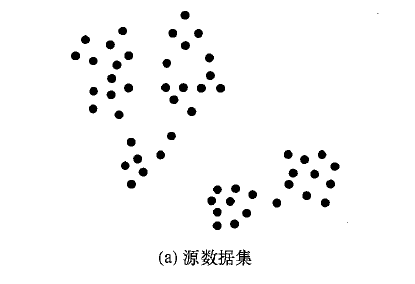
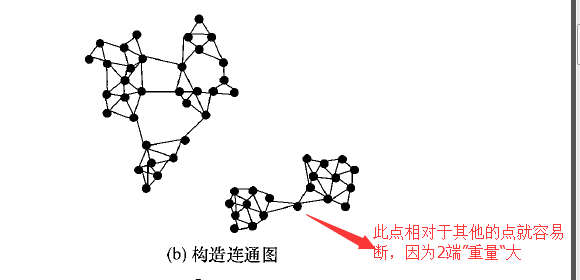
算法的大的方向的阶段为2个阶段,第一个是根据坐标点的位置距离关系形成连通图。第二个阶段是将形成的多个连通图,进行逐一的分裂。图形化的表示过程如下,方便大家理解。
这么看来,和chameleon算法还是非常类似的。第一个步骤可以采用我的上一篇文章中用到的dbscan算法的思路,去深度优先搜索尽可能大的范围的点集,然后再用边将他们连接起来。这个如果不清楚的话,可以点击我的上一篇文章进行查阅。在这里会给定一个距离阈值l,这样就会生出基于距离l的连通图集。在上图中,就生成了2个连通图集,上面的一个和下面的一个。下面主要讲一下分裂的机理和过程,这也是整个算法的创新点和难点所在。
分裂的原理
分裂的原理采用了类似于扁担挑重物的形式,每一条边类似于一个扁担,坐标点在这里就是一个个的重物,如果扁担的2端的重物都非常重,那么扁担就容易断,于是就会分裂。举个例子如下:
但是我们要怎么去衡量一条边能不能够被分裂的标准呢,在这里定义了2个概念,承受系数t和分裂阈值landa。承受因为t就是要分裂的2部分中的较轻的一端的重量/连接2部分的边数,意思就是平均每条边所要承受的点的个数。公式如下:
t=min{W1,W2}/n,W1,W2为分割后的2部分的点的个数,n为2连接2部分的边的数量。
理解了这个,就很好分裂阈值了,分裂阈值就是当前针对全部的连通图,每条边的承受状况指数,你可以理解为就是总坐标点数/总边数。但是我们在这里采用更科学的方式进行计算,大意还是如上面描述的那样:
注意这里的x和y的关系,与上面的已经不一样了,至于这个公式为什么就不比刚刚的那个要好,就不是本文所论述的范畴了。截止到这里,我们就能得出一个比较条件了,就是当根据某条边进行分割的时候,如果此时计算出来的承受系数大于等于分裂阈值的时候,就表明此边是可以被分割掉的,也就是说,此时的连通图可以继续被拆分掉。算法的伪代码如下:
main()
{
Result r;
for-each每个连通图G
{
Graph[] graphs;
graphs = splitGraph(G)
r.add(graphs)
}
}
splitGraph(连通图G)
{
//默认不能被划分
int canDivied=0;
for(m从2到Pnum/2) //Pnum为连通图中的坐标点数
{
//将原图进行分割
Graph2 subGraph2 =G,removeM();
Graph1 subGraph1 = G;
//此函数会判断承受系数是否大于此时的分裂阈值
if(canDivide(subGraph1, subGraph2))
{
//改变标签
canDivied=1;
//继续递归的划分子图1,子图2
split(subGraph1);
split(subGraph2);
}
}
if(canDivided == 0)
{
//说明不能在分割了,为一个聚类,加入结果集中
addToResult()
}
}
上面的伪代码是自己想出来的,与论文原文所描述略有不同,我对其中加入了个人的思考和改进的地方,首先一点都是一样的,就是分裂一定是递归进行的,后一次的划分是建立在前一次划分的基础上进行的。以上就是第二阶段所做的事情,然后再次把目标转向问题本身,因为此问题是基于连通图的,所以在这里我用了边的数组表示,他其实是一个无向图,我还是用了id对id的形式来表示是否存在连接2点的边。下面也是算法的代码实现,也非常的重要哦(请仔细看里面的一些实现细节)。
算法的实现
首先是数据的点输入graphData.txt(格式:id 横坐标 纵坐标):
0 1 12 1 3 9 2 3 12 3 4 10 4 4 4 5 4 1 6 6 1 7 6 3 8 6 9 9 8 3 10 8 10 11 9 2 12 9 11 13 10 9 14 11 12总共15个点。
坐标点类Point.java:
package DataMining_CABDDCC;
/**
* 坐标点类
* @author lyq
*
*/
public class Point implements Comparable<Point>{
//坐标点id号,id号唯一
int id;
//坐标横坐标
Integer x;
//坐标纵坐标
Integer y;
//坐标点是否已经被访问(处理)过,在生成连通子图的时候用到
boolean isVisited;
public Point(String id, String x, String y){
this.id = Integer.parseInt(id);
this.x = Integer.parseInt(x);
this.y = Integer.parseInt(y);
}
/**
* 计算当前点与制定点之间的欧式距离
*
* @param p
* 待计算聚类的p点
* @return
*/
public double ouDistance(Point p) {
double distance = 0;
distance = (this.x - p.x) * (this.x - p.x) + (this.y - p.y)
* (this.y - p.y);
distance = Math.sqrt(distance);
return distance;
}
/**
* 判断2个坐标点是否为用个坐标点
*
* @param p
* 待比较坐标点
* @return
*/
public boolean isTheSame(Point p) {
boolean isSamed = false;
if (this.x == p.x && this.y == p.y) {
isSamed = true;
}
return isSamed;
}
@Override
public int compareTo(Point p) {
if(this.x.compareTo(p.x) != 0){
return this.x.compareTo(p.x);
}else{
//如果在x坐标相等的情况下比较y坐标
return this.y.compareTo(p.y);
}
}
}
连通图类Graph.java:
package DataMining_CABDDCC;
import java.util.ArrayList;
import java.util.Collections;
/**
* 连通图类
*
* @author lyq
*
*/
public class Graph {
// 坐标点之间的连接属性,括号内为坐标id号
int[][] edges;
// 连通图内的坐标点数
ArrayList<Point> points;
// 此图下分割后的聚类子图
ArrayList<ArrayList<Point>> clusters;
public Graph(int[][] edges) {
this.edges = edges;
this.points = getPointByEdges(edges);
}
public Graph(int[][] edges, ArrayList<Point> points) {
this.edges = edges;
this.points = points;
}
public int[][] getEdges() {
return edges;
}
public void setEdges(int[][] edges) {
this.edges = edges;
}
public ArrayList<Point> getPoints() {
return points;
}
public void setPoints(ArrayList<Point> points) {
this.points = points;
}
/**
* 根据距离阈值做连通图的划分,构成连通图集
*
* @param length
* 距离阈值
* @return
*/
public ArrayList<Graph> splitGraphByLength(int length) {
int[][] edges;
Graph tempGraph;
ArrayList<Graph> graphs = new ArrayList<>();
for (Point p : points) {
if (!p.isVisited) {
// 括号中的下标为id号
edges = new int[points.size()][points.size()];
dfsExpand(p, length, edges);
tempGraph = new Graph(edges);
graphs.add(tempGraph);
} else {
continue;
}
}
return graphs;
}
/**
* 深度优先方式扩展连通图
*
* @param points
* 需要继续深搜的坐标点
* @param length
* 距离阈值
* @param edges
* 边数组
*/
private void dfsExpand(Point point, int length, int edges[][]) {
int id1 = 0;
int id2 = 0;
double distance = 0;
ArrayList<Point> tempPoints;
// 如果处理过了,则跳过
if (point.isVisited) {
return;
}
id1 = point.id;
point.isVisited = true;
tempPoints = new ArrayList<>();
for (Point p2 : points) {
id2 = p2.id;
if (id1 == id2) {
continue;
} else {
distance = point.ouDistance(p2);
if (distance <= length) {
edges[id1][id2] = 1;
edges[id2][id1] = 1;
tempPoints.add(p2);
}
}
}
// 继续递归
for (Point p : tempPoints) {
dfsExpand(p, length, edges);
}
}
/**
* 判断连通图是否还需要再被划分
*
* @param pointList1
* 坐标点集合1
* @param pointList2
* 坐标点集合2
* @return
*/
private boolean needDivided(ArrayList<Point> pointList1,
ArrayList<Point> pointList2) {
boolean needDivided = false;
// 承受系数t=轻的集合的坐标点数/2部分连接的边数
double t = 0;
// 分裂阈值,即平均每边所要承受的重量
double landa = 0;
int pointNum1 = pointList1.size();
int pointNum2 = pointList2.size();
// 总边数
int totalEdgeNum = 0;
// 连接2部分的边数量
int connectedEdgeNum = 0;
ArrayList<Point> totalPoints = new ArrayList<>();
totalPoints.addAll(pointList1);
totalPoints.addAll(pointList2);
int id1 = 0;
int id2 = 0;
for (Point p1 : totalPoints) {
id1 = p1.id;
for (Point p2 : totalPoints) {
id2 = p2.id;
if (edges[id1][id2] == 1 && id1 < id2) {
if ((pointList1.contains(p1) && pointList2.contains(p2))
|| (pointList1.contains(p2) && pointList2
.contains(p1))) {
connectedEdgeNum++;
}
totalEdgeNum++;
}
}
}
if (pointNum1 < pointNum2) {
// 承受系数t=轻的集合的坐标点数/连接2部分的边数
t = 1.0 * pointNum1 / connectedEdgeNum;
} else {
t = 1.0 * pointNum2 / connectedEdgeNum;
}
// 计算分裂阈值,括号内为总边数/总点数,就是平均每边所承受的点数量
landa = 0.5 * Math.exp((1.0 * totalEdgeNum / (pointNum1 + pointNum2)));
// 如果承受系数不小于分裂阈值,则代表需要分裂
if (t >= landa) {
needDivided = true;
}
return needDivided;
}
/**
* 递归的划分连通图
*
* @param pointList
* 待划分的连通图的所有坐标点
*/
public void divideGraph(ArrayList<Point> pointList) {
// 判断此坐标点集合是否能够被分割
boolean canDivide = false;
ArrayList<ArrayList<Point>> pointGroup;
ArrayList<Point> pointList1 = new ArrayList<>();
ArrayList<Point> pointList2 = new ArrayList<>();
for (int m = 2; m <= pointList.size() / 2; m++) {
// 进行坐标点的分割
pointGroup = removePoint(pointList, m);
pointList1 = pointGroup.get(0);
pointList2 = pointGroup.get(1);
// 判断是否满足分裂条件
if (needDivided(pointList1, pointList2)) {
canDivide = true;
divideGraph(pointList1);
divideGraph(pointList2);
}
}
// 如果所有的分割组合都无法分割,则说明此已经是一个聚类
if (!canDivide) {
clusters.add(pointList);
}
}
/**
* 获取分裂得到的聚类结果
*
* @return
*/
public ArrayList<ArrayList<Point>> getClusterByDivding() {
clusters = new ArrayList<>();
divideGraph(points);
return clusters;
}
/**
* 将当前坐标点集合移除removeNum个点,构成2个子坐标点集合
*
* @param pointList
* 原集合点
* @param removeNum
* 移除的数量
*/
private ArrayList<ArrayList<Point>> removePoint(ArrayList<Point> pointList,
int removeNum) {
//浅拷贝一份原坐标点数据
ArrayList<Point> copyPointList = (ArrayList<Point>) pointList.clone();
ArrayList<ArrayList<Point>> pointGroup = new ArrayList<>();
ArrayList<Point> pointList2 = new ArrayList<>();
// 进行按照坐标轴大小排序
Collections.sort(copyPointList);
for (int i = 0; i < removeNum; i++) {
pointList2.add(copyPointList.get(i));
}
copyPointList.removeAll(pointList2);
pointGroup.add(copyPointList);
pointGroup.add(pointList2);
return pointGroup;
}
/**
* 根据边的情况获取其中的点
*
* @param edges
* 当前的已知的边的情况
* @return
*/
private ArrayList<Point> getPointByEdges(int[][] edges) {
Point p1;
Point p2;
ArrayList<Point> pointList = new ArrayList<>();
for (int i = 0; i < edges.length; i++) {
for (int j = 0; j < edges[0].length; j++) {
if (edges[i][j] == 1) {
p1 = CABDDCCTool.totalPoints.get(i);
p2 = CABDDCCTool.totalPoints.get(j);
if (!pointList.contains(p1)) {
pointList.add(p1);
}
if (!pointList.contains(p2)) {
pointList.add(p2);
}
}
}
}
return pointList;
}
}
算法工具类:
package DataMining_CABDDCC;
import java.io.BufferedReader;
import java.io.File;
import java.io.FileReader;
import java.io.IOException;
import java.text.MessageFormat;
import java.util.ArrayList;
/**
* 基于连通图的分裂聚类算法
*
* @author lyq
*
*/
public class CABDDCCTool {
// 测试数据点数据
private String filePath;
// 连通图距离阈值l
private int length;
// 原始坐标点
public static ArrayList<Point> totalPoints;
// 聚类结果坐标点集合
private ArrayList<ArrayList<Point>> resultClusters;
// 连通图
private Graph graph;
public CABDDCCTool(String filePath, int length) {
this.filePath = filePath;
this.length = length;
readDataFile();
}
/**
* 从文件中读取数据
*/
public void readDataFile() {
File file = new File(filePath);
ArrayList<String[]> dataArray = new ArrayList<String[]>();
try {
BufferedReader in = new BufferedReader(new FileReader(file));
String str;
String[] tempArray;
while ((str = in.readLine()) != null) {
tempArray = str.split(" ");
dataArray.add(tempArray);
}
in.close();
} catch (IOException e) {
e.getStackTrace();
}
Point p;
totalPoints = new ArrayList<>();
for (String[] array : dataArray) {
p = new Point(array[0], array[1], array[2]);
totalPoints.add(p);
}
// 用边和点构造图
graph = new Graph(null, totalPoints);
}
/**
* 分裂连通图得到聚类
*/
public void splitCluster() {
// 获取形成连通子图
ArrayList<Graph> subGraphs;
ArrayList<ArrayList<Point>> pointList;
resultClusters = new ArrayList<>();
subGraphs = graph.splitGraphByLength(length);
for (Graph g : subGraphs) {
// 获取每个连通子图分裂后的聚类结果
pointList = g.getClusterByDivding();
resultClusters.addAll(pointList);
}
printResultCluster();
}
/**
* 输出结果聚簇
*/
private void printResultCluster() {
int i = 1;
for (ArrayList<Point> cluster : resultClusters) {
System.out.print("聚簇" + i + ":");
for (Point p : cluster){
System.out.print(MessageFormat.format("({0}, {1}) ", p.x, p.y));
}
System.out.println();
i++;
}
}
}
算法调用类Client.java:
package DataMining_CABDDCC;
/**
* 基于连通图的分裂聚类算法
* @author lyq
*
*/
public class Client {
public static void main(String[] agrs){
String filePath = "C:\\Users\\lyq\\Desktop\\icon\\graphData.txt";
//连通距离阈值
int length = 3;
CABDDCCTool tool = new CABDDCCTool(filePath, length);
tool.splitCluster();
}
}
算法的输出:
聚簇1:(6, 9) (8, 10) (9, 11) (10, 9) (11, 12) 聚簇2:(1, 12) (3, 9) (3, 12) (4, 10) 聚簇3:(4, 4) (4, 1) (6, 3) (6, 1) (8, 3) (9, 2)
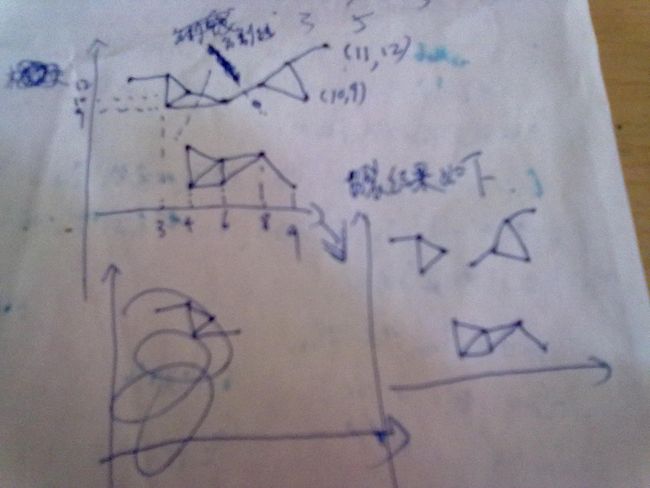
图形化的展示结果如下,一张是连通图的有效边(就是e[i][j]=1)的情况,后张图是分裂的聚类结果:
图片有点大,就没有处理了,大家将就着看吧.....
算法的遗漏点和优点
其实这个算法我在实现的时候,其实少考虑了很多东西,首先一个是构造连通图的时候,可以从示例的图线中看出,最后的图应该是一个闭环图,而我通过类似于DBSCAN算法会导致最边界的点会暴露在外面,形成不了闭环,与题目所要求的会有点不符。还有1点是划分部分坐标点的时候,我默认是从左往右,从下往上的优先级的顺序进行划分,但是我觉得更加合理的方式应该是怎样的。还有1个算法的缺点是总是在不停的比较中,时间开销比较大。算法非常的新颖,用了图的思想去做聚类的实现,而且用了类似于扁担挑重物的原理运用到数据挖掘中,不愧是一篇好论文。像我目前就只能是站在巨人的肩膀上,做点小东西罢了....