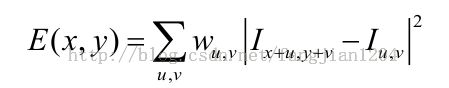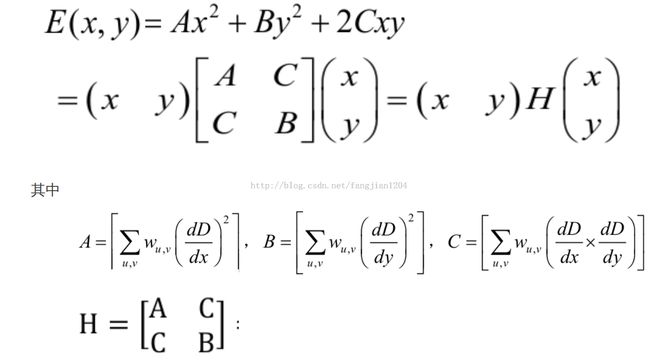Harris角点检测算法

Harris算法是使用比较多的角点算法之一，opencv中实现的角点检测算法就是Harris和它的改进。

Harris角点检测的原理：

Harris 角点最初由Harris在A combined corner and edge detector一文中提出,该文实际上是对Moravec算法思想的改进。Harris角点最直观的解释是,在两个相互垂直的方向,都有较大变化的点。通俗一点描述该算法就是：First find a gray value changes the direction of maximum variation, and then calculate the gray value in the direction perpendicular to the direction of the value. If the two variation is greater than a given threshold, for the corner；如果只有一个大于阀值，则为边缘；如果都不大于，则为内部平滑点。由于两个互相垂直的最大变化方向可以出现在任何方向，所以Harris算法可以统计任意方向的灰度值变化，而且对旋转具有不变性。

这一直观认识的数学描述如下。

首先,定义自相关函数:

该相关函数和moravec中的一样，但是Harris首先对Wu,v进行了替换，使用的是高斯窗口，另一方面对灰度值差进行了泰勒展开，然后进行推导。

注：该公式中的x,y与moravec中的意义不同。moravec算法中表示的像素的坐标，而这里表示的变化量，例如这里(1,0)表示窗口右移一个单位后灰度值的变化，这样E ( x, y ) 实际上刻画的是图像偏移造成的窗口内像素的平均变化。显然,窗口固定之后E ( x, y ) 为x, y的函数。所以Harris的思想是对E(x,y)求极大值，所得的(x,y)代表灰度值变化最大的方向；然后求出该方向的垂直方向的灰度值变化，最后比较得出结论。为了加快求解速度，Harris对E(x,y)中的灰度值变化部分进行泰勒展开。若令D= I (x +u , y + v) − I (u ,v ),则有D ( x, y )可以在原点(0, 0) Taylor展开,最后得到

A 可以理解为 x变化时,窗口内图像一阶差分的平方和。同理,B可以理解为 y方向一阶差分的平方和,C理解为 x方向一阶差分与y方向一阶差分的乘积。一介差分可以根据sobel算子求的，Harris给的差分公式是卷积公式，

个人理解为用函数差代替差分，即x方向的差分近似等于1/2[f(x+1,y)-f(x-1,y)].这样可以很容易求得每个像素的H矩阵。求得H矩阵的目的是因为Harris通过计算发现，E(x,y)的两个互相垂直的灰度值变化方向是H的特征向量方向，而相应的特征值就是其灰度值变化量。即它的解为H的最大特征值λ1的特征向量( x1 , y1 )。并且有此时E ( x1 , y1 ) = λ1。由矩阵论知识,(x1 , y1 )的垂直方向为H的另一个特征值λ2对应的特征向量。相应的有E ( x2 , y2 ) =λ2。所以只要求得H的两个特征值就可以判断该点是不是角点。由于H是一个hessian矩阵，求其特征值比较有很简单的方法，从而可以快速得到角点的判断。具体方法不在详述。