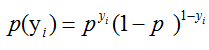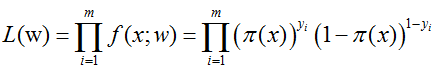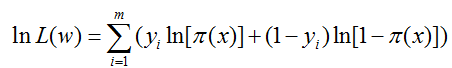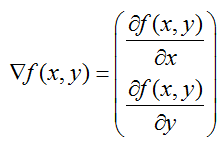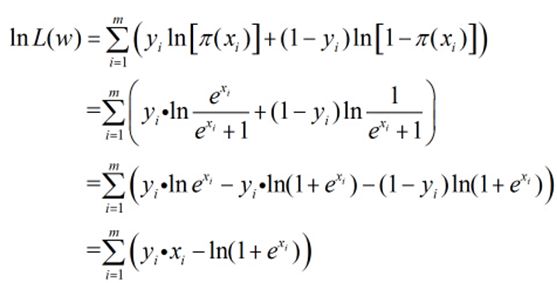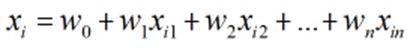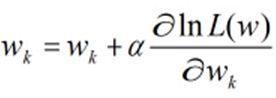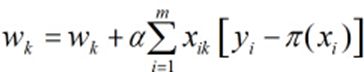机器学习之旅---logistic回归
一、logistic回归分析简介
logistic回归是研究观察结果(因变量)为二分类或多分类时,与影响因素(自变量)之间关系的一种多变量分析方法,属于概率型非线性回归。
利用logistic回归进行分类的主要思想是:根据现有数据对分类边界线建立回归公式,以此进行分类。这里“回归”是指通过最优化方法找到最佳拟合参数集,作为分类边界线的方程系数。通过分类边界线进行分类,具体说来就是将每个测试集上的特征向量乘以回归系数(即最佳拟合参数),再将结果求和,最后输入到logistic函数(也叫sigmoid函数),根据sigmoid函数值与阈值的关系,进行分类。也就是说logistic分类器是由一组权值系数组成,最关键的问题就是如何求得这组权值。
在流行病学研究中,logistic回归常用于分析疾病与各种危险因素间的定量关系。这次将利用logistic回归预测病马的死亡率,病马样本有368个,每个样本有21个特征点,即21种危险因素。接下来,本文首先介绍利用梯度上升法及改进的随机梯度上升法寻找最佳回归系数,然后用matlab实现基于logistic回归的病马死亡率预测。
二、如何寻找最优化参数
1.logistic回归模型
给定n个特征x=(x1,x2,…,xn),设条件概率P(y=1|x)为观测样本y相对于事件因素x发生的概率,用sigmoid函数表示为:
那么在x条件下y不发生的概率为:
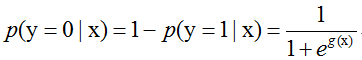
假设现在有m个相互独立的观测事件y=(y1,y2,…,ym),则一个事件yi发生的概率为(yi= 1)
那么现在就成了,已知总体事件Y是服从上述概率密度的连续型随机变量:
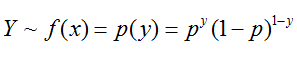
由于logistic分类器是由一组权值系数组成的,最关键的问题就是如何获取这组权值。而f(x)中x是由权值向量与特征向量相乘的结果,即g(x)表示,其中特征向量是随机变量,只有向量w是参数,所以权值向量w可以通过极大似然函数估计获得,并且Y~f(x;w)
【回忆一下似然函数的性质】
1.似然函数是统计模型中参数的函数。给定输出x时,关于参数θ的似然函数L(θ|x)(在数值上)等于给定参数θ后变量X的概率:L(θ|x)=P(X=x|θ)
2.似然函数的重要性不是它的取值,而是当参数变化时概率密度函数到底是变大还是变小。对于同一个似然函数,如果存在一个参数值,使得它的函数值得到最大,那么这个值就是最为合理的参数值。
3.极大似然函数:似然函数取得最大值表示相应的参数能够使得统计模型最为合理
那么对于上述m个观测事件,其联合概率密度函数,即似然函数为:
现在,我们的目标是求出使这一似然函数的值最大的参数估,也就是求出参数w1,w2,…,wn,使得L(w)取得 最大值。对L(w)取对数:
由于w有n+1个,根据n+1的对wi的偏导数方程求解w比较不靠谱。可以考虑使用牛顿-拉菲森迭代和梯度上升方法求解。梯度上升算法和牛顿迭代相比,收敛速度慢,因为梯度上升算法是一阶收敛,而牛顿迭代属于二阶收敛。
2.梯度上升法
梯度上升法基于的思想是要找到某函数的最大值,最好的方法是沿着该函数的梯度方向探寻。函数f(x,y)的梯度可以如下表示,前提是函数f(x,y)必须在待计算的点上有定义并且可微。
在梯度上升法中,待计算点沿梯度方向每移动一步,都是朝着函数值增长最快的方向。若移动的步长记作a,则梯度算法的迭代公式如下:
迭代停止条件为:迭代次数达到某个指定的值或者算法达到某个可以允许的误差范围。现在继续对刚才的似然函数进行推到:
其中,
根据梯度上升算法有,
进一步得到,
接下来将根据上述推到,实现一个利用logistic回归得到分类边界的例子,由于不擅长python,我索性用matlab改写了。现在有100个样本点及对应分类标签,每个样本点有2个特征。【文本文件中有100行*3列数据,自己导入matlab,做成*.mat文件即可】
clc;
clear;
load x
load y
load label
[r,c] = size(x);
A = ones(1,r)';
A = [A x y];
L = label;
alpha = 0.001;
maxCycles = 500;
weights = ones(1,3)';
for k=1:1:maxCycles
h = sigmoid(A*weights,r);
error = (L - h);
weights = weights + alpha * A' * error;
end
%%画图
for k = 1:1:r
hold on
if L(k,1) == 1
plot(A(k,2),A(k,3),'r+');
else
plot(A(k,2),A(k,3),'b*');
end
end
%%画分割线
hold on
dx = -3:3;
dy = (-weights(1)-weights(2)*dx)/weights(3);
plot(dx,dy,'k-','lineWidth',3);
function result = sigmoid(inX,r)
result = [];
for k = 1:1:r
result(k,1) = 1.0 / (1 + exp(-inX(k,1)));
end
end
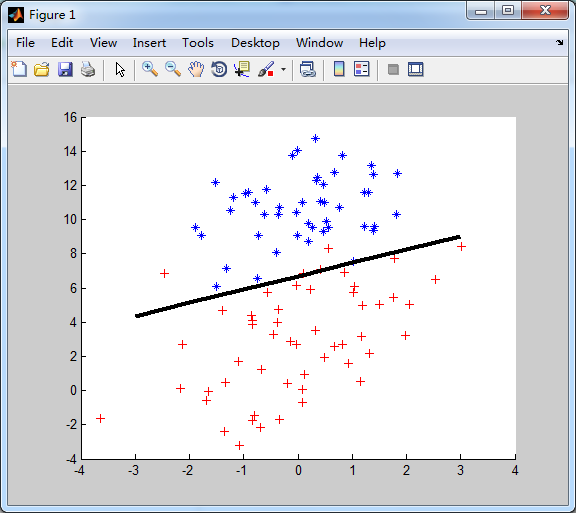
分类边界:
注:为了方便计算,这里为每个样本点新增一列特征X0,都为1.0,否则分类边界将过零点,不准确了。
分界线的方程: w0 * x0 + w1 * x1 + w2 * x2 = 0
3.改进的梯度上升法
梯度上升法在每次更新回归系数时都需要遍历整个数据集,该方法在处理100个左右数据集时效率尚可,但如果有10亿样本和成千上万的特征,那么这个方法的计算量就太大了。改进方法是一次仅用一个点来更新回归系数。它是一种在线学习算法【即:可以在新的样本到来时对分类器进行增量式更新。】,每一次处理的数据的操作被称为“批处理”
clc;
clear;
load x
load y
load label
[r,c] = size(x);
A = ones(1,r)';
A = [A x y];
L = label;
alpha = 0.01;
weights = ones(1,3)';
for k = 1:1:r
h = sigmoid2(sum(A(k,:,:)*weights));
error = L(k) - h;
weights = weights + alpha * error * A(k,:,:)';
end
%%画图
for k = 1:1:r
hold on
if L(k,1) == 1
plot(A(k,2),A(k,3),'r+');
else
plot(A(k,2),A(k,3),'b*');
end
end
%%画分割线
hold on
figure(1);
dx = -3:3;
dy = (-weights(1)-weights(2)*dx)/weights(3);
plot(dx,dy,'k-','lineWidth',3);
%画各种迭代次数
figure(2);
weights = ones(1,3)';
for j=1:1:200
for k = 1:1:r
h = sigmoid2(sum(A(k,:,:)*weights));
error = L(k) - h;
weights = weights + alpha * error * A(k,:,:)';
end
hold on
subplot(3,1,1);
%axis([1 2000 -3 1]);
plot(j,weights(1),'r.');
hold on
subplot(3,1,2);
plot(j,weights(2),'b.');
hold on
subplot(3,1,3);
plot(j,weights(3),'k.');
end
function result = sigmoid2(inX) result = 1.0 / (1 + exp(-inX)); end
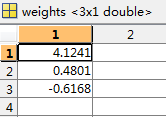
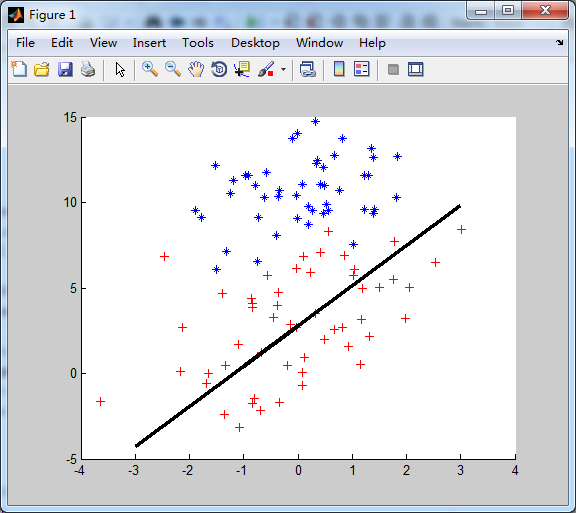
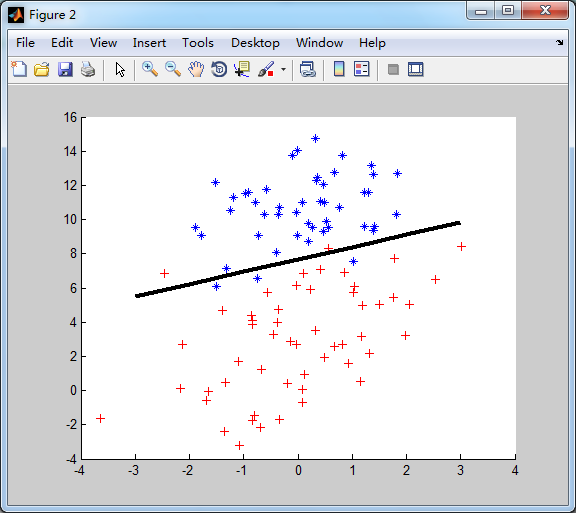
分类边界:
从上图结果来看,分类器错分的样本点很多。原因是,梯度上升法的分类边界是在整个数据集上经过500次迭代得到的。目前改进的梯度上升法,没有迭代。
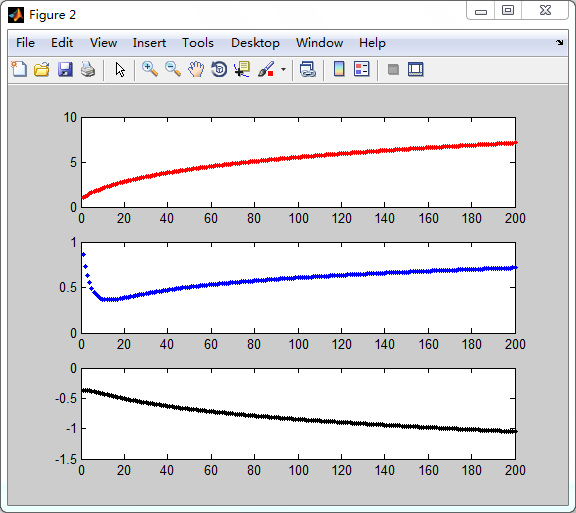
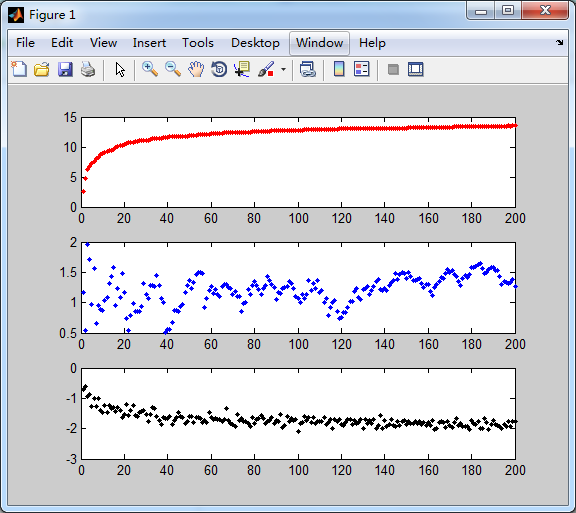
此外,一个判断优化算法优劣的可靠方法是看它是否收敛,也就是说参数是否达到了稳定值,是否还会不断变化。现在让随机梯度法在数据集上运行200次,得到下图:
200次迭代过程中,3个参数的收敛情况:从上到下分别对应w0,w1,w2【不知道书上的图是怎么画的,反正我这边是这样的】
产生上述波动的原因,是存在一些不能正确分类的样本点【数据集并非线性可分】,在每次迭代时会引发数据的变化。下面将通过随机梯度法,来避免波动,从而收敛到某个值,并加快收敛速度。
4.随机梯度上升法
改进有两个地方:
。alpha在每次迭代的时候都会调整,alpha的值是不断变小的,但永远不能减小到零,保证在多次迭代之后,新数据仍然有一定的影响。
。通过随机选取样本来更新回归系数,另外增加了一个迭代次数参数。
clc;
clear;
load x
load y
load label
[r,c] = size(x);
A = ones(1,r)';
A = [A x y];
L = label;
weights = ones(1,3)';
figure(1);
tmp = [];
for j = 1:1:200
for k = 1:1:r
alpha = 4/(j+k+1) + 0.01;
index = floor(random('unif',1,r,1,1));
% k = find(tmp == index);
% if isempty(k)
% tmp = [tmp index];
% else
% continue;
% end
h = sigmoid2(sum(A(index,:)*weights));
error = L(index) - h;
weights = weights + alpha * error * A(index,:)';
end
hold on
subplot(3,1,1);
%axis([1 2000 -3 1]);
plot(j,weights(1),'r.');
hold on
subplot(3,1,2);
plot(j,weights(2),'b.');
hold on
subplot(3,1,3);
plot(j,weights(3),'k.');
end
%%画图
figure(2);
for k = 1:1:r
hold on
if L(k,1) == 1
plot(A(k,2),A(k,3),'r+');
else
plot(A(k,2),A(k,3),'b*');
end
end
%%画分割线
hold on
dx = -3:3;
dy = (-weights(1)-weights(2)*dx)/weights(3);
plot(dx,dy,'k-','lineWidth',3);
function result = sigmoid2(inX) result = 1.0 / (1 + exp(-inX)); end
这边我很质疑《机器学习python实战》书上的描述和截图,首先我根本没看见之前算法的周期性波动和高频,反而在随机算法中看到了。【他坐标轴axis改动过】
另外一个,就是每次随机选取样本后,要从样本里踢出的,我这么改了,收敛速度的确快了很多,但是,分类边界线错误没有改变很多。所以我不踢出了
分类边界线:
各个参数的迭代结果:【只有w0是收敛比较快的,w1,w2收敛了嘛?】
这种随机梯度算法相比第一种梯度上升法的计算量:第一种要500次循环,每次300次乘法,现在是200次循环,每次3次乘法1次加法,从矩阵的运算变成值的运算。运算量的确减少了。
三、病马预测实例
368个样本,21个特征点,选300个作为训练用,68个作为测试
书中扯到数据丢失的处理问题,我看了下文本数据,他都弄好了,不要我们自己处理了。
大概意思就是:特征点丢失,用0代替;类标签丢失,整条记录舍弃。所以只剩299个样本做训练,67个作为测试样本了。
现在将完整展示,如何通过logistic回归进行分类预测:
clc;
clear;
load train
load test
[r,c] = size(test);
T_data = train(:,1:21);
T_lab = train(:,22);
P_data = test(:,1:21);
P_lab = test(:,22);
%训练
weights = train_weights(T_data,T_lab,500);
%预测
% fuck = 0;
% for shit = 1:1:10
err_count = 0;
for k=1:1:r
predict = my_classify(P_data,weights);
if predict ~= P_lab(k)
err_count = err_count + 1;
end
end
err_rate = err_count / r;
disp('the error rate of this test is :');
err_rate
% fuck = fuck + err_rate;
% end
% disp('the average error rate of 10 time test is:');
% fuck/10
function weights = train_weights(Data,Lab,iter)
[r,c] = size(Data);
weights = ones(1,c)';
for j = 1:1:iter
for k = 1:1:r
alpha = 4/(j+k+1) + 0.01;
ctime = datestr(now, 30);%取系统时间
tseed = str2num(ctime((end - 5) : end)) ;%将时间字符转换为数字
rand('seed', tseed) ;%设置种子,若不设置种子则可取到伪随机数
index = randint(1,1,r) + 1;
h = sigmoid2(sum(Data(index,:)*weights));
error = Lab(index) - h;
weights = weights + alpha * error * Data(index,:)';
end
end
end
function result = sigmoid2(inX)
result = 1.0 / (1 + exp(-inX));
end
function result = my_classify(Data, weights)
prob = sigmoid(sum(Data*weights));
if prob > 0.5
result = 1;
else
result = 0;
end
end
function a = sigmoid(inX)
a = 1.0 / (1 + exp(-inX));
end
比较蛋疼的问题是,每次跑matlab,随机数都一样。。。我已经把系统时间当seed了啊。。。
今天就写到这里吧。谁能解决matlab随机数问题的,可以留言。