opencv学习_13 (trajkovic 角点检测)
来源:http://blog.csdn.net/songzitea/article/details/13614977
背景引言
本节主要内容来源于是由 Miroslav Trajkovic和Mark Hedley[1]在1998年提出Trajkovic算子,其论文为FastCorner Detection.和Trajkovic Operator (4-Neighbours)[3](注:本节图片主要是来源于此)。Trajkovic算子角点提取方法存在价值是在角点提取的效果上,它优于同时期的其他角点(如Moravec角点,Harris角点)提取方法,同时,从算法的运行速度角度而言,它比同是期的其他角点提取方法要快很多。
基本理论
作者对角点的定义,与Moravec角点、 Harris 角点的定义是一样的:图像灰度值在各个方向变化都比较大的点,即认为是角点。角点量的定义也类似于Moravec,即角点量的是在各个方向上灰度变化的最小值(当在某个方向上,灰度值的变化最小,并且这个最小值也大于某某个设定的阈值,那么认为这个点就是一个角点)。与Moravec 相比 ,Trajkovic 的性能更好,因为Trajkovic通过使用像素插值的方法比较每一个方向上的灰度值变化程度,而moravec只有限个方向的比较,与harris相比,两都效果差不多,但是Trajkovic的速度远快于haris.
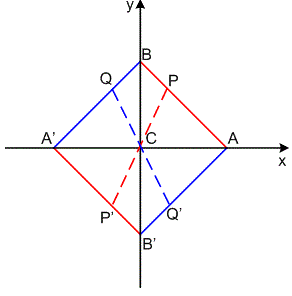
Trajkovic在速度方面的表现于决定它能够应用对实时要求比较高的系统中。但是Trajkovic也有缺点是它不具备旋转不变性,对噪声比较敏感,对对角点的响应值比较大等。对于这些缺点也会有相应的方法,但不能完全的解决这些缺点。Trajkovic算子计算角点量是在一个小的圆形窗口内,并且考虑了所有通过圆心的直线,即计算了每一个可能的方向上的灰度值变化程度)。假设用C表示圆的圆心,那么通过圆心C的任意一条直线会与圆在两个交点,如图1所示:
Figure 1: Notation for Trajkovic Operator
那么,Trajkovic对角点量的定义是
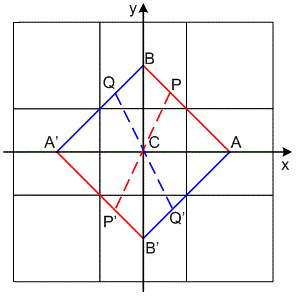
C(x,y)表示的是图像I上,任意一点(x,y)处的角点量。这个公式能断出是否是角点。点(x,y)在图像目的位置有四种情况。如下图所示:
第一情况:点(x,y)在内部区域:此时经点(x,y)位中心的圆形窗中完全在一个比较平坦的区域,或者大部分的圆形窗口是在这个平坦区域的(如上图A所示)。这种情况下,至少存大一条直线过中心点C的直线使得Ic约等于Ip和Ic约等于Ip‘,根据角点量计算公式,计算出的C(x,y)一定是一个很小的值,那么就可以排除点(x,y)不是角点。并且,大多数的情况下,会有多个这样的点P存大,使得对噪声一定的承受能力。
第二情况:点(x,y)在边缘上:此时圆形窗口的中心点(x,y)刚好落在边缘上(如上图B所示)。仅存在一个点对P,P'使得Ic约等于Ip和Ic约等于Ip‘。在理想状况下,根据角点量的公式计算出来的角点量C(x,y)是比较小的。但是由于只存在一个条这样直线,所以容易受到噪声的干扰。
第三情况:点(x,y)在角点上:当圆窗口的中心(x, y)位于角点上时(如上图C 所示)。任意一条通过点(x,y)与圆相交的交点P、P', P、P' 中至少有一个点的灰度值与中心的点的灰度值差别比较大。所以计算出来的角点量也比较大(大于设定的阈值,所以会被认为是角点)。
第四情况:点(x,y)在一个孤立点上:如果在孤立点上(如上图D所示),对于每一个直线上的Ip, Ip’,都分与Ic的值相差比较大,此时计算出的角点量也比较大。此时这个点是噪声,但是由于角点量比较大,会被认为是角点。为了削除这种噪声的影响,可以先使用高斯平滑进行去噪。
根据上面的分析,Trajkovic 受噪声的影响比较大,所以,可以先实现高斯平滑去噪再使用Trajkovic算子进行角点检测。
角点量的计算方法
目前,关于Trajkovic计算角点量的并未具体介绍如何时计算。首先,如下图2所示,水平方向的灰度值变化量rA,垂直方向的灰度值变化量rB很容易计算。
如何计算任意一个方向上灰度值的变化程度呢?首先,我们角点量就取其最小值即可:
Figure 2: Interpixel positions Figure3: Interpixel approximation for a 3x3 window using 4-neighbours
现在,我们可将问题可以转换为,任意一条通过点C 的直线与圆的交点是P,P',Q,Q'即可:
把公式(2)代入公式(1) 中即可:
那么,![]() 最小值是即可结论是
最小值是即可结论是
多格算法(Multigrid Algorithm)
角点可以分为两类:几何角点和纹理角点。几何角点是由图像中物体边缘的相交。而纹理角点有由物体表面的纹理产生的角点(如:草地,衣服的纹理等)。通常情况下,一幅图像中的几何角点的数量要远少于纹理角点。多格算法的目的是希望能多检测到几何角点,少检测到纹理点。因Trajkovic 认为几何角点比纹理角点更加的稳定。所以,从实践使用来看,减少纹理角点是合理的。
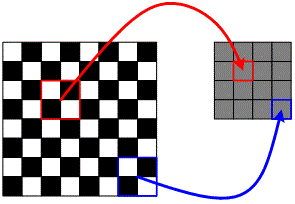
经过观察发现,纹理角点一般都是非常的密集,并且是在一个很小区域内灰度值发生变化,所以,采用把原图缩小以后,再来提取角点,通过缩小图像,可以消除区域内灰度值的变换。缩小图像的方法不是使用插值法,而是使用平均法。如下图所示:
Trajkovic角点检测,首先使用多格法对原如图像进行缩小,这样不仅能够减少检测到纹理角点数目,而且加快了Trajkovic角点检测的速度,在Trajkovic角点检测缩小版的图像上,使用角为简单的角点量计算公式初步判断是不是侯选角点。如果是,再到原始图像上进一步判定。
Figure 4: Corner points detected at different image resolutions
如图4所示,原始的大小是256*256,图像中有一片草地,而草地上的角点,对于我们进行角点匹配时,是没有什么意义。当把图像缩小到128*128时,草地上的角点已经消除了。当然,图像也不能缩小太多,否则,几何角点也会消失,当缩小到64*64时,部分几何角点也消失了。
算法流程

代码:
#include <iostream>
#include "cv.h"
#include "highgui.h"
#include "cxcore.h"
using namespace std;
void getTrajkovic4NCorner(IplImage* src,IplImage* srcResize , float T1 , float T2 ,CvSeq* corners,int maximumSize)
{
int x,y,maxChar=255,scaleX = src->width/srcResize->width,scaleY = src->height/srcResize->height;
IplImage* srcResizeMap ,*srcMap;
srcResizeMap = cvCreateImage(cvGetSize(srcResize),8,1); // 用来保存缩小图像的角点量
srcMap = cvCreateImage(cvGetSize(src),32,1); // 用来保存源图像计算得到的角点量
cvZero(srcMap);
cvZero(srcResizeMap);
for( y=1;y<srcResize->height-1;y++)
{
uchar* preRow = (uchar*)(srcResize->imageData + (y-1)*srcResize->widthStep);
uchar* curRow = (uchar*)(srcResize->imageData + y*srcResize->widthStep);
uchar* nextRow = (uchar*)(srcResize->imageData + (y+1)*srcResize->widthStep);
uchar* MapData = (uchar*)(srcResizeMap->imageData + y*srcResizeMap->widthStep);
for(x=1;x<srcResize->width-1;x++)
{
int IC,IA,IB,IAA,IBB;
int rA,rB,C_Simple;
// curRow[x]是uchar型,而IC是int型,如果直接赋值int类型的其它三个字节可能会产生随机值
IC = curRow[x]&maxChar;
IA = curRow[x+1]&maxChar;
IAA = curRow[x-1]&maxChar;
IB = preRow[x]&maxChar;
IBB = nextRow[x]&maxChar;
rA = (IA-IC)*(IA-IC) + (IAA-IC)*(IAA-IC);
rB = (IB-IC)*(IB-IC) + (IBB-IC)*(IBB-IC);
C_Simple = rA < rB ? rA : rB;
if(C_Simple > T1)
{
MapData[x]=1;
}
}
}
for( y=1;y<srcResize->height-1;y++)
{
uchar* srcResizeMapData = (uchar*)(srcResizeMap->imageData + y*srcResizeMap->widthStep);
//uchar* srcMapData = (uchar*)(srcMap->imageData + y*srcMap->widthStep);
for(x=1;x<srcResize->width-1;x++)
{
if(srcResizeMapData[x]==0)
{
continue;
}
int originX,originY,IC,IA,IB,IAA,IBB;
int rA,rB,C_Simple;
originX = x*scaleX;
originY = y*scaleY;
uchar* srcPreRow = (uchar*)(src->imageData + (originY-1)*src->widthStep);
uchar* srcCurRow = (uchar*)(src->imageData + originY*src->widthStep);
uchar* srcNextRow = (uchar*)(src->imageData + (originY+1)*src->widthStep);
IC = srcCurRow[originX]&maxChar;
IA = srcCurRow[originX+1]&maxChar;
IAA = srcCurRow[originX-1]&maxChar;
IB = srcPreRow[x]&maxChar;
IBB = srcNextRow[x]&maxChar;
rA = (IA-IC)*(IA-IC) + (IAA-IC)*(IAA-IC);
rB = (IB-IC)*(IB-IC) + (IBB-IC)*(IBB-IC);
C_Simple = rA < rB ? rA : rB;
if(C_Simple>T2)
{
float B1,B2,C,A,B,C_InterPixel;
B1 = (IB-IA)*(IA-IC)+(IBB-IAA)*(IAA-IC);
B2 = (IB-IAA)*(IAA-IC)+(IBB-IA)*(IA-IC);
C = rA;
B = B1<B2 ? B1 : B2;
A = rB-rA-2*B;
if(B<0 &&(A+B)>0)
{
C_InterPixel = C-(B*B)/A;
}
else
{
C_InterPixel=C_Simple;
}
if(C_InterPixel>T2)
{
float* srcMapData = (float*)(srcMap->imageData + originY*srcMap->widthStep);
srcMapData[originX]=C_InterPixel;
//cvSetReal2D(srcMap,originY,originX,C_InterPixel);
}
}
}
}
//计算局部极大值 及 极大值是否大于阈值
int beginY,endY,beginX,endX;
int halfWinSize = maximumSize/2;
beginY = halfWinSize;
endY = srcMap->height - halfWinSize;
beginX = halfWinSize;
endX = srcMap->width - halfWinSize;
for(y=beginY;y<endY;)
{
for(x=beginX;x<endX;)
{
//寻找局部极大值 及其位置信息
float maxValue=0;
int flag = 0 ;
CvPoint maxLoc;
maxLoc.x = -1;
maxLoc.y = -1;
//首先计算以点(x,y)位中心的maximumSize*maximumSize的窗口内部的局部极大值
for(int winy=-halfWinSize;winy<=halfWinSize;winy++)
{
for(int winx=-halfWinSize;winx<=halfWinSize;winx++)
{
float value ;
value = cvGetReal2D(srcMap,y+winy,x+winx);
//计算该窗口内 最大值 保存到max 并保存其坐标到maxLoc
if(value>maxValue)
{
maxValue = value;
maxLoc.x = x+winx;
maxLoc.y = y+winy;
flag = 1;
}
}
}
//如果找到局部极大值 并且该值大于预先设定的阈值 则认为是角点
if(flag==1 && maxValue>T2)
{
cvSeqPush(corners,&maxLoc);
}
x = x+halfWinSize;
}
y = y + halfWinSize;
}
cvReleaseImage(&srcResizeMap);
cvReleaseImage(&srcMap);
}
int main(int argc,char* argv[])
{
//相关变量
int scale = 2;
IplImage* src,*srcGray,*srcGrayResize;
CvMemStorage* mem = cvCreateMemStorage(0);
CvSeq* TrajkovicPoints;
src = cvLoadImage("E:\\study_opencv_video\\lesson17_2\\2.jpg");//源图像
srcGray = cvCreateImage(cvGetSize(src),8,1);
if(!src)
{
cout << "src is null" << endl;
return 0;
}
cvCvtColor(src,srcGray,CV_BGR2GRAY);
srcGrayResize = cvCreateImage(cvSize(srcGray->width/scale,srcGray->height/scale),8,1);
cvResize(srcGray,srcGrayResize);//请将resize修改为多格算法
//Trajkovic 4 邻域角点角点保存的空间 角点坐标保存在一个序列中
TrajkovicPoints = cvCreateSeq(0,sizeof(CvSeq),sizeof(CvPoint),mem);
//进行Trajkovic 4 邻域角点检测
int T1=120,T2=150,localArea = 8; // localArea 是局部极大值抑制时窗口的大小
getTrajkovic4NCorner(srcGray,srcGrayResize,T1,T2,TrajkovicPoints,localArea);
//获取每一个角点的坐标
for(int x=0;x<TrajkovicPoints->total;x++)
{
//获取第x个角点的坐标
CvPoint* pt = (CvPoint*)cvGetSeqElem(TrajkovicPoints,x);
//以角点坐标为中心 绘制一个半径为5的圆
cvCircle(src,*pt,2,cvScalar(255,0,255,0));
}
//显示图像
cvNamedWindow("dst");
cvShowImage("dst",src);
cvWaitKey(0);
//释放资源
cvReleaseImage(&src);
cvReleaseImage(&srcGray);
cvReleaseImage(&srcGrayResize);
cvReleaseMemStorage(&mem);
return 0;
}英文链接: http://kiwi.cs.dal.ca/~dparks/CornerDetection/trajkovic.htm