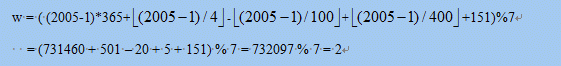算法系列之十七:日历生成算法-中国公历(格里历)(下)
【接上篇】
上述计算星期的方法虽然步骤简单,但是每次都要计算两个日期的时间差,不是非常方便。如果能够有一个公式可以直接根据日期计算出对应的星期岂不是更好?幸运的是,这样的公式是存在的。此类公式的推导原理仍然是通过两个日期的时间差来计算星期,只是通过选择一个特殊的日期来简化公式的推导。这个所谓的特殊日期指的是某一年的12月31日这天刚好是星期日这种情况。选择这样的日子有两个好处,一个是计算上可以省去计算标准日期这一年的剩余天数,另一个是计算出来的日期差余数是几就是星期几,不需要再计算星期的差值。人们知道公元元年的1月1日是星期一,那么公元前1年的12月31日就是星期日,用这一天作为标准日期,就可以只计算整数年的时间和日期所在的年积累的天数,这个星期公式就是:
w = (L * 366 + N * 365 + D) % 7 (公式 2)
公式中的L是从公元元年到y年m月d日所在的年之间的闰年次数,N是平常年次数,D是y年内的积累天数。将整年数y - 1 = L + N带入上式,可得:
w = ( (y - 1) * 365 + L + D) % 7 (公式 3)
根据闰年规律,从公元元年到y年之间的闰年次数是可以计算出来的,即:
将L带入公式2,得到星期w的最终计算公式:
还以2005年5月31日为例,利用公式5计算w的值为:
得到2005年5月31日是星期二,和前面的计算方法得到的结果一致。根据上述分析,可得写出使用公式5计算星期的算法实现:
|
146 int TotalWeek(int year, int month, int day) 147 { 148 int d = CalcYearPassedDays(year, month, day); 149 int y = year - 1; 150 int w = y * DAYS_OF_NORMAL_YEAR + y / 4 - y / 100 + y / 400 + d; 151 152 return w % 7; 153 } |
公式5的问题在于计算量大,不利于口算星期结果。于是人们就在公式5的基础上继续推导更简单的公式。德国数学家克里斯蒂安·蔡勒(Christian Zeller, 1822- 1899)在1886年推导出了著名的为蔡勒(Zeller)公式:
![]()
对计算出的w值除以7,得到的余数就是星期几,如果余数是0,则为星期日。蔡勒公式中各符号的含义如下:
w :星期;
c :世纪数 – 1的值,如21世纪,则 = 20;
m :月数,的取值是大于等于3,小于等于14。在蔡勒公式中,某年的1月和2月看作上一年的13月和14月,比如2001年2月1日要当成2000年的14月1日计算;
y :年份,取公元纪念的后两位,如1998年, = 98,2001年, = 1;
d :某月内的日数
为了方便口算,人们通常将公式6中的![]() 一项改成
一项改成![]()
。目前人们普遍认为蔡勒公式是计算某一天是星期几的最好的公式。但是蔡勒公式有时候可能计算出的结果是负数,需要对结果+7进行修正。比如2006年7月1日,用蔡勒公式计算出的结果是 -1,实际上这天是星期六。根据前面分析的结果整理出的蔡勒公式算法实现如下:
|
155 int ZellerWeek(int year, int month, int day) 156 { 157 int m = month; 158 int d = day; 159 160 if(month <= 2) /*对小于2的月份进行修正*/ 161 { 162 year--; 163 m = month + 12; 164 } 165 166 int y = year % 100; 167 int c = year / 100; 168 169 int w = (y + y / 4 + c / 4 - 2 * c + (13 * (m + 1) / 5) + d - 1) % 7; 170 if(w < 0) /*修正计算结果是负数的情况*/ 171 w += 7; 172 173 return w; 174 } |
蔡勒公式(公式6)和前面提到的公式5都只适用于格里历法。罗马教皇在1582年修改历法,将10月5日指定为10月15日,从而正式废止儒略历法,开始启用格里历法。因此,上述求星期几的公式只适用于1582年10月15日之后的日期,对于1582年将10月4日之前的日期,蔡勒也推导出了适用与儒略历法的星期计算公式:
![]()
公式7适用于对1582年10月4日之前的日期计算星期,1582年10月5日与1582年10月15日之间的日期是不存在的,因为它们都是同一天。
格里历历法简单,除二月外每月天数固定,二月则根据是否是闰年确定是28天还是29天,每天的星期数可以通过蔡勒公式(公式6)计算,有了这些信息,就可以按照一定的排版格式将某一年的日历打印出来。排版打印的算法非常简单,就是按照顺序打印12个月的月历,因此,打印月历的函数就是输出算法的重点。代码没什么特别之处,就是用一些小技巧确定每个月的第一天的开始位置,打印月历的核心代码如下:
|
229 void PrintMonthCalendar(int year, int month) 230 { 231 int days = GetDaysOfMonth(year, month); /*确定这个月的天数*/ 232 if(days <= 0) 233 return; 234 235 PrintMonthBanner(nameOfMonth[month - 1]); 236 PrintWeekBanner(); 237 int firstDayWeek = ZellerWeek(year, month, 1); 238 InsertRowSpace(firstDayWeek); 239 int week = firstDayWeek; 240 int i = 1; 241 while(i <= days) 242 { 243 printf("%-10d", i); 244 if(week == 6) /*到一周结束,切换到下一行输出*/ 245 { 246 SetNextRowStart(); 247 } 248 i++; 249 week = (week + 1) % 7; 250 } 251 } |
GetDaysOfMonth()函数其实就是从daysOfMonth表中查一下每月的天数,如果是闰年,则对二月的天数修正(+1),daysOfMonth表定义如下:
int daysOfMonth[MONTHES_FOR_YEAR] = { 31, 28, 31, 30, 31, 30, 31, 31, 30, 31, 30, 31};
计算星期不必对每一天都计算一次,只要对每个月的第一天计算一次就可以了,以后的日期可以用 week = (week + 1) % 7 直接推算出星期几。下面就是我们的算法打印输出的效果:
********************************************************************************
Calendar of 2012
********************************************************************************
----------January----------
Sunday Monday Tuesday Wednesday Thursday Friday Saturday
1 2 3 4 5 6 7
8 9 10 11 12 13 14
15 16 17 18 19 20 21
22 23 24 25 26 27 28
29 30 31
----------February----------
Sunday Monday Tuesday Wednesday Thursday Friday Saturday
1 2 3 4
5 6 7 8 9 10 11
12 13 14 15 16 17 18
19 20 21 22 23 24 25
26 27 28 29
----------March----------
Sunday Monday Tuesday Wednesday Thursday Friday Saturday
1 2 3
4 5 6 7 8 9 10
11 12 13 14 15 16 17
18 19 20 21 22 23 24
25 26 27 28 29 30 31
……
小知识2:儒略历和格里历
在公元1582年10月15日之前,人们使用的历法是源自古罗马的儒略历,儒略历的置闰规则就是四年一闰,但是没有计算每年多出来的0.0078天,这样从公元前46年到公元1582年一共累积多出了10天,为此,当时的教皇格里十三世将1582年10月5日人为指定为10月15日,并开始启用新的置闰规则,这就是后来沿用至今的格里历。
小知识3:约化儒略日
由于儒略日数字位数太多,国际天文联合会于1973年8月决定对其修正,采用约化儒略日(MJD)进行天文计算,定义MJD = JD – 2400000.5,MJD相应的起始点是1858年11月17日 0:00。
小知识4:1752年9月到底是怎么回事儿
如果你用的操作系统是unix或linux,在控制台输入以下命令:
#cal 9 1752
你会看到这样一个奇怪的月历输出:
September 1752
Su Mo Tu We Th Fr Sa
1 2 14 15 16
17 18 19 20 21 22 23
24 25 26 27 28 29 30
1752年的9月缺了11天,到底怎么回事儿?这其实还是因为从儒略历到格里历的转换造成的。1582年10月5日,罗马教皇格里十三世宣布启用更为精确的格里历,但是整个欧洲大陆并不是所有国家都立即采用格里历,比如大英帝国就是直到1752年9月议会才批准采用格里历,所以大英帝国及其所有殖民地的历法一直到1752年9月才发生跳变,“跟上”了格里历。德国和荷兰到了1698年才采用格里历,而俄罗斯则直到1918年革命才采用格里历。Linux的cal指令起源与最初AT&T的UNIX,当然采用的是美国历法,但是美国历史太短,再往前就只能采用英国历法,所以cal指令的结果就成了这样。对于采用格里历的国家来说,只要知道1582年10月发生了日期跳变就行了,可以不用关心1752年9月到底是怎么回事儿。但是对于研究历史和考古的人来说,就必需要了解这个历史,搞清楚每个欧洲国家改用格里历的年份,否则就可能在一些问题上出错。在欧洲研究历史,你会发现很多事件都是有多个时间版本的,比如大科学家牛顿的生日就有两个时间版本,一个是按照儒略历历法的1642年12月25日,另一个是格里历历法的1643年1月4日,对于英国人来说,1752年之前都是按照儒略历计算的,所以英国的史书可能会记载牛顿出生在圣诞节,这也没什么可奇怪的。