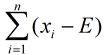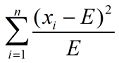卡方检验（Chi square statistic）

卡方检验是一种检验两个变量独立性的方法。本文将介绍其理论并给出其应用在LBP特征匹配中的例子。

卡方检验最基本的思想就是通过观察实际值与理论值的偏差来确定理论的正确与否。具体做的时候常常先假设两个变量确实是独立的（行话就叫做“原假设”），然后观察实际值（也可以叫做观察值）与理论值（这个理论值是指“如果两者确实独立”的情况下应该有的值）的偏差程度，如果偏差足够小，我们就认为误差是很自然的样本误差，是测量手段不够精确导致或者偶然发生的，两者确确实实是独立的，此时就接受原假设；如果偏差大到一定程度，使得这样的误差不太可能是偶然产生或者测量不精确所致，我们就认为两者实际上是相关的，即否定原假设，而接受备择假设。

那么用什么来衡量偏差程度呢？假设理论值为E（这也是数学期望的符号哦），实际值为x，如果仅仅使用所有样本的观察值与理论值的差值x-E之和：

来衡量，单个的观察值还好说，当有多个观察值x₁，x₂，x₃的时候，很可能x₁-E，x₂-E，x₃-E的值有正有负，因而互相抵消，使得最终的结果看上好像偏差为0，但实际上每个都有偏差，而且都还不小！此时很直接的想法便是使用方差代替均值，这样就解决了正负抵消的问题，即使用

这时又引来了新的问题，对于500的均值来说，相差5其实是很小的（相差1%），而对20的均值来说，5相当于25%的差异，这是使用方差也无法体现的。因此应该考虑改进上面的式子，让均值的大小不影响我们对差异程度的判断，式（1）：

上面这个式子已经相当好了。实际上这个式子就是开方检验使用的差值衡量公式。当提供了数个样本的观察值x₁，x₂，……x_i ，……x_n之后，代入到式（1）中就可以求得开方值，用这个值与事先设定的阈值比较，如果大于阈值（即偏差很大），就认为原假设不成立，反之则认为原假设成立。

那如果将卡方检验用在图像特征匹配上，可以将已有图像的每个特征作为均值（或者多个图像的特征取平均值作为均值）E，而待匹配图像特征作为变量​x_i，按照式子（1）进行独立性检验，如果检验结果小于阈值，则可认为待匹配图像和原图像是相同的。

举个例子，在LBP人脸识别中，每个图像可以被分割成大小相同的N块区域，在这些小区域中利用LBP提取直方图特征，这样每个图像就得到了很多直方图信息，设待匹配图像的直方图为S_i,j，已知图像的直方图为M_i,j，其中i=1,2，...，N为图像的某块小区域，j为小区域内直方图的某一列的值，则两幅图像的相似性为：

其中wj是每块小区域的权重，比如在人脸区域中，眼睛嘴巴等区域包含的信息量更为丰富，那么这些区域的权重就可以设置的大一些。上式中的分母部分为S_i,j+M_i,j，可能是考虑到相同人脸在不同照片中的差异性。

以上理论部分参考自：http://www.blogjava.net/zhenandaci/archive/2008/08/31/225966.html