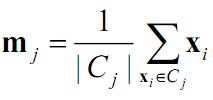数据挖掘十大经典算法学习之K均值（K-means）聚类算法
基本概念
• 监督学习vs.无监督学习
Ø 监督学习: 发现数据属性与类别属性之间的关联模式。
– 通过利用这些模式来预测未知数据实例的类别属性。
Ø 无监督学习: 没有类别属性.
– 希望探索数据以发现其中的内在结构。
无监督学习包括聚类、关联规则等。
• K-均值聚类算法是最著名的划分聚类算法。
Ø 设实例的集合D为{x1,x2, …, xn}， xi = (xi1,xi2, …,xir) 是实数空间的向量，r表示数据的属性数目（数据空间的维数）。
• K-均值算法把给定的数据划分成k个聚类。
Ø 每个聚类有一个聚类中心。
Ø k的值由用户指定。
step1: 随机选择k个数据点作为初始聚类中心。
step2: 计算每个数据点与各聚类中心的距离，将数据点分配给与其距离最小的聚类中心，直至所有数据均被分配。
step3: 重新计算现有聚类的聚类中心。
step4: 重复step2~step3直到满足收敛条件。
聚类的表示
1. 聚类中心
2. 分类模型
3. 平凡值
距离函数
• 聚类中心：所有向量除以个数。
• 数据点和聚类中心之间的距离：欧几里得距离
//距离公式有很多种，对于不同类型的数据集，如何选用合适的距离公式？
终止条件
• 没有数据点被重新分配给不同的聚类。
• 聚类中心不再变化。
• 误差平方和（SSE）局部最小。
SSE：所有数据点离其聚类中心的距离。用来度量聚类的好坏。
Ci 表示第j个聚类, mj 是聚类Cj 的聚类中心（Cj所有数据点的均值向量）,dist(x,mj) 是数据点 x与 聚类中心mj. 之间的距离。
//如何证明k-means会收敛？
优势&劣势
优势：
Ø 简洁：容易被理解且容易被实现。
Ø 效率：时间复杂度O(tkn)是线性的,t是循环次数，k是聚类的个数，n是数据点的个数。
//另一说法，为O(n2)。因为聚类的个数k最大可以达到n。
劣势：
Ø 只能应用于均值能够被定义的数据集上。
Ø 用户需事先指定聚类数目k。
Ø 算法对异常值十分敏感。
Ø 对初始种子敏感。
Ø 不适用于超维椭球体的聚类。
数据标准化
强制各个属性都在一个相同的范围内变化。
聚类的评估
• 基于外部信息：
Ø 分类数据集评估 e.g.鸢尾花label。
Ø 熵
Ø 纯度：一个聚类中仅包含一个类别的数据的程度。
• 基于内部信息：
Ø 聚类内紧密度（SSE）
Ø 聚类间分离度
Acknowledgements&References：
感谢陈W老师主持的系列DM讲座。理论知识部分摘自于刘冰的《Web数据挖掘》。