《数据结构与算法分析》回溯算法之博弈——三连棋(tic tac toe)人机对战AI设计(αβ枝减)
前言:
这次的回溯算法实在是太有意思了,不过刚刚接触的时候确实不容理解,极小极大策略,αβ枝减看了好几遍才明白整个过程。实现的时候又发现还有细节不明白,想明白之后对于整体的认识又加深了一步。
编码的过程反而没有太大的问题,只有再判断平局的时候,写错了判断的条件,导致没有平局存在,花了点时间调试就解决了。
我的github:
我实现的代码全部贴在我的github中,欢迎大家去参观。
https://github.com/YinWenAtBIT
介绍:
三连棋介绍:
一、规则:
游戏双方交替下子,知道棋盘上没有空余格或者直到分出胜负。胜利条件是任意一方棋子横竖斜练成一条线。未达成胜利则是平局。
二、算法思想:
1. 使用回溯法思想,每个点落子之后,可以达到的最优结果返回,将所有可以落子的格子都考察过后,选择其中最符合自己要求的点。
2. 极小极大策略,设电脑胜利为1,平局为0, 人类胜利为-1, 那么电脑要找出所有点之中极大的那个,人类要找出所有点中极小的那个。
3. 使用递归的方式来下棋,轮到电脑下棋时,电脑选一个点,然后模拟人类下棋,再电脑下棋,直到分出胜负或者平局,模拟人类和电脑下棋时,遵循各自的极小极大策略。
三、 核心算法伪代码:
电脑思考伪代码中,在落子之前,先判断上一轮模拟人的落子是否已经出了结果,没有出结果则继续寻找最优落子点。
先设有一个最差的结果-1.即电脑输,然后找到一个空格,落子,然后再递归模拟人类,电脑,直到分出胜负,那么这是返回的该点的结果为Response,判断该结果是否大于value,即找极大值的过程。循环完毕就返回该值和落子点。
模拟人类的伪代码基本和电脑的一样,先判断电脑落子是否分出胜负,在循环寻找然value最小的值,即人类胜利,电脑输的值
四、αβ枝减
做到了这一步,确实已经得到了可以运行的程序。但是这个程序运行结果良好,是由于一共只有9个点可以选择导致的,所以反复循环递归,直到分出胜负的开销也并不大。不过,即使只有9个点,如果电脑先手,此时需要考虑的情况就有97162种情况了,再多几个空格,就没法模拟下去,会导致栈溢出。
因此,我们在这里需要考虑,在什么情况下,可以缩减需要测试的点,即判断一半时,已经确定该循环求出的结果,对于上层的最后结果已经没有影响的时候。
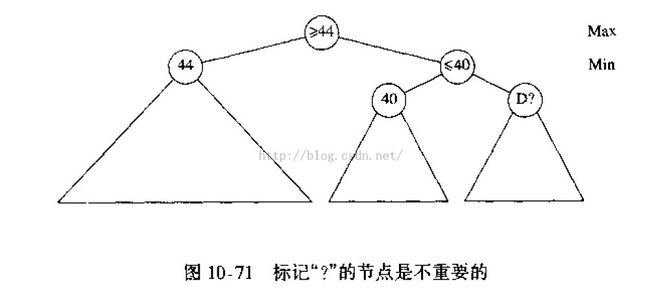
首先是alpha枝减:
当前正在进行的是右手边那个<=40判断的那一层, 即寻找每个格子返回给它的值中的最小值,Min层,此层在模拟人落子。
Min层的上层是模拟电脑,上层对每一个子层返回来的极小值(它的下一步是人下棋,人寻找最小的值),寻找其中最大的一个,该图中,Max层,即电脑层已经获得了左边人类返回来的极小值44,那么现在电脑可以取到44,如果没有比它更大的结果的话。
此时,电脑在运行下一层时,把它已经找到的最大极小值44,告诉了右边的Min层,即模拟人类下棋的程序。那么如果右边模拟的Min层找到所有结果中的极小值,大于44,那么上一层的电脑将会选择它的值,如果小于44,上一层不会取它返回的结果。
那么此时,Min层的下一层,左边的模拟电脑,返回了它找到的极大值,40,这个值是小于Min的上一层电脑,已经找到的极小值44的,那么如果最终Min层取40,那么上层电脑不会取Min'层返回的结果。那么现在Min层还能不能取大于40的值呢?答案是不能的,因为Min层是寻找所有结果里的最小值的,那么D返回的结果大于40,Min层取40,小于40,Min层取一个更小的结果,更加小于44了。Max层的电脑就不会取它了。
所以这时,就没有必要判断D的结果了。因为不可能大于40 了,所以Min层结果一定小于等于40了。Max层有更好的选择44。
这就是alpha枝减,当人类模拟的结果小于上层电脑传来的alpha时,就可以停止模拟了。
那么beta枝减,正好相反,当电脑模拟的结果大于上层人类传来的beta时,上层人类会选择最小的结果,所以电脑不用继续寻找最大值了。
beta枝减博弈树如下图:
此时电脑模拟层Max找到最大的极小值已经是68了,大于上层Min找到最小值44,所以C的结果已经不重要了。
电脑的beta枝减伪代码如下:
游戏逻辑:
先确定是否要玩游戏,玩游戏的话谁先手:int main()
{
char game =' ';
while(game != 'n' && game != 'N')
{
cout<<"you wanna play a game? y/n: ";
cin >>game;
if(game == 'y' || game == 'Y')
{
srand(time(NULL));
char first;
cout<<"you wanna play first? y/n: ";
cin >>first;
if(first == 'y' || first == 'Y')
manFirst();
else
comFirst();
}
}
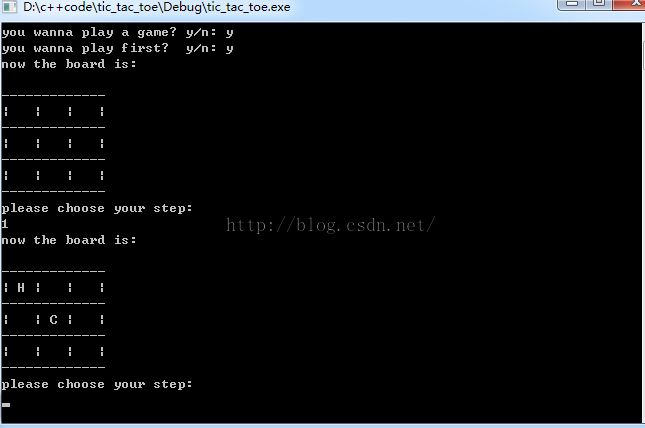
}人类先手,则读取人类的落子,然后电脑判断最佳落子,然后落子,在轮到人类,知道分出胜负或者平局。
void manFirst()
{
BoardType Board ={' ', ' ', ' ', ' ', ' ', ' ', ' ', ' ', ' '};
int BestStep = -1;
int Value;
int Result = -2;
int humanstep;
while(Result == -2)
{
std::cout<<"now the board is:\n";
DrawBoard(Board);
do
{
std::cout<<"please choose your step: "<<std::endl;
std::cin>>humanstep;
humanstep -= 1;
}while(!IsEmpty(Board, humanstep/3, humanstep%3));
Place(Board, humanstep/3, humanstep%3, 'H');
if(ImmediateHumanWin(Board))
Result = -1;
else if(!FullBoard(Board))
{
FindComMove(Board, &BestStep, &Value, -1, 1);
// FindComMove(Board, &BestStep, &Value);
Place(Board, BestStep/3, BestStep%3, 'C');
if(ImmediateComWin(Board))
Result = 1;
}
else
Result = 0;
}
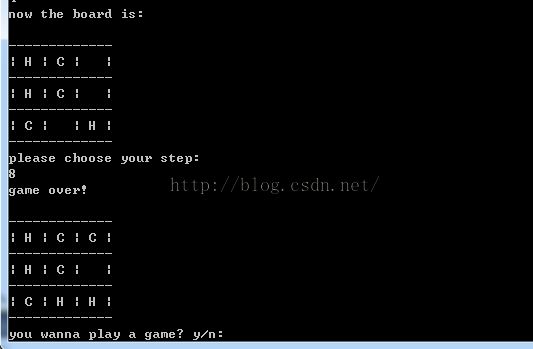
std::cout<<"game over!"<<std::endl;
DrawBoard(Board);
}
电脑先手:
void comFirst()
{
BoardType Board ={' ', ' ', ' ', ' ', ' ', ' ', ' ', ' ', ' '};
int BestStep = -1;
int Value;
int Result = -2;
int humanstep;
int firststep = random();
Place(Board, 2*firststep/3, 2*firststep%3, 'C');
while(Result == -2)
{
if(!FullBoard(Board))
{
std::cout<<"now the board is:\n";
DrawBoard(Board);
do
{
std::cout<<"please choose your step: "<<std::endl;
std::cin>>humanstep;
humanstep -= 1;
}while(!IsEmpty(Board, humanstep/3, humanstep%3));
Place(Board, humanstep/3, humanstep%3, 'H');
if(ImmediateHumanWin(Board))
Result = -1;
else
{
FindComMove(Board, &BestStep, &Value, -1, 1);
// FindComMove(Board, &BestStep, &Value);
Place(Board, BestStep/3, BestStep%3, 'C');
if(ImmediateComWin(Board))
Result = 1;
}
}
else
Result = 0;
}
std::cout<<"game over!"<<std::endl;
DrawBoard(Board);
}核心模拟部分,与算法完全相同,只需要实现即可:
void FindComMove(BoardType Board, int *BestMove, int *Value, int Alpha, int Beta)
{
int Dc, i, j, Response;
if(FullBoard(Board))
*Value = Draw;
else if(ImmediateHumanWin(Board))
*Value = ComLoss;
else
{
*Value = Alpha;
for(i =0; i<9 && *Value < Beta; i++)
{
if(IsEmpty(Board, i/3, i%3))
{
Place(Board, i/3, i%3, 'C');
FindHumanMove(Board, &Dc, &Response, *Value, Beta);
Unplace(Board, i/3, i%3);
if(Response > *Value)
{
*Value = Response;
*BestMove = i;
}
}
}
}
}人类寻找电脑返回结果中最小的一个:
void FindHumanMove(BoardType Board, int *BestMove, int *Value, int Alpha, int Beta)
{
int Dc, i, j, Response;
if(FullBoard(Board))
*Value = Draw;
else if(ImmediateComWin(Board))
*Value = ComWin;
else
{
*Value = Beta;
for(i =0; i<9 && *Value > Alpha; i++)
{
if(IsEmpty(Board, i/3, i%3))
{
Place(Board, i/3, i%3, 'H');
FindComMove(Board, &Dc, &Response, Alpha, *Value);
Unplace(Board, i/3, i%3);
if(Response < *Value)
{
*Value = Response;
*BestMove = i;
}
}
}
}
}
代码中使用alpha beta枝减,减少了判断的次数。
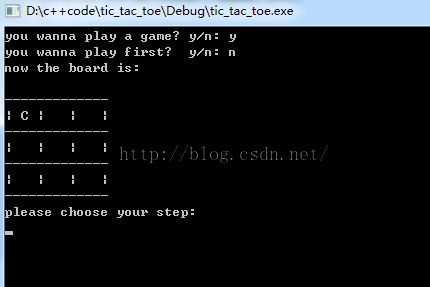
电脑先选择了1号顶点,我故意选择一个对角点:
总结:
这一次难点主要在理解alpha beta枝减,弄明白了,写出代码来很容易。这一次反了一个错误就是判断平局逻辑写反了,结果调试的时候,递归到棋盘都满了,才发现原来达不到平局的结果。改完之后,电脑立刻就变聪明了,这个算法真是特别有意思。