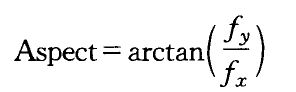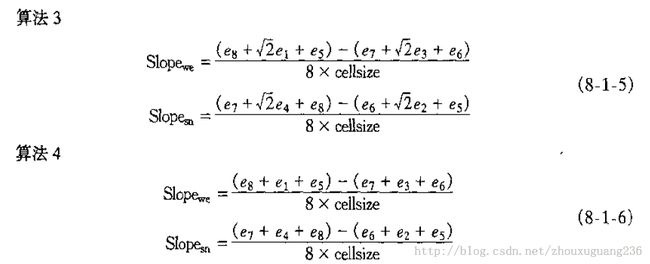基于OpenCL的数字地形分析之坡度坡向提取
基于OpenCL的数字地形分析之坡度坡向提取
又有一段时间没有发表博客了，可能最近工作有点忙。今天就把最近的学习和研究成果和大家分享一下。对于GIS稍微有点了解的人都知道地形分析中的坡度和坡向，这是数字地形分析中最基本的分析了，对于数字地形分析中很多计算都是邻域分析，所以非常适合数据并行。
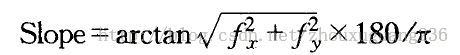
其中fx和fy分别代表x和y方向上的高程变化率。坡度有两种表示方法，一种是坡度角，另外一种是坡度百分比，即高程增量与水平增量的百分比。
此外，还需要包装两个结构用于传参数；
//坡度的表达方式
typedef enum
{
DEGREE_SLOPE, //度数方式
PERCENT_SLOPE //百分比方式
}SLOPE_TYPE;
//坡度算法结构体
struct SlopeOption
{
double dbNsres; //南北方向分辨率
double dbEwres; //东西方向分辨率
SLOPE_TYPE slopeType; //坡度方式
} ;
最终，我设计的计算坡度的函数如下：
bool ExtractSlope(const char* pszDEMfile,const char* pszOutSlpoeFile,const char* pszFormat, SLOPE_TYPE eSlopeType ,double dbScale)
pszDEMfile为输入DEM数据；pszOutSlpoeFile为输出坡度数据；pszFormat为输出影像格式；
eSlopeType是坡度的类型，即坡度百分比还是坡度角度；dbScale可选，一般情况下为1.0。
在GIS和遥感领域，一般情况下，栅格数据都是非常大的，不可能将所有像素全部读进来一次性处理，所以就必然涉及到影像分块。关于影像分块，对于不同的算法可以采用不同的策略，其主要策略如下：
对于单点运算，即运算过程之和当前计算的像素相关的算法，分块可以按照按照行来分块，也可以矩形分块，类似于地图切片。一般来说，影像是按照行优先的顺序类存储的，所以按照行分块可以减少文件指针移动的次数，提高速度。
对于邻域相关的运算，如本文提到的坡度、卷积等运算，也可以按照行分块或者矩形分块。但是要注意一个问题，这样简单的分块会导致块与块之间的结果不连续。针对这种情况，为了缝合块边缘的结果，可以再读取数据的时候边缘的数据重复读取，这样就保证了最后合成的结果具有连续性，也就是说保证有一定的重叠度，一般重叠度为邻域窗口大小的一半。
还有一种情况是全局相关的运算，如求图像的最值，这个也可以采用上述两种方法都可以，即分好块之后，最后求得各个块的最值。
总结一下，分块的思想体现了算法设计中的分治法思想，即所谓的分而治之。
对于本文，我采用的分块读取、分块处理和分块写入数据的思路如下：
1、按照行来分块，窗口大小为3，所以块之间重叠一个像素；
2、对于分块后只有一个块的情况，不需要做特别处理
3、对于分块后有多个块的情况，也根据块的索引做不同处理：为了说明方便，我先定义几个变量
//实际的块的大小
int nRealWidth = nXsize;
int nRealHeight = nSubHeight;
//读取数据块的大小
int nReadWidth = nXsize;
int nReadHeight = nSubHeight;
int nYOffset = i*nSubHeight; //某一块读取数据的Y方向上的偏移量
nSubHeight为分块的高
a、对于第0个块，块的实际读取数据的高度nReadHeight为nReadHeight += 1;，即向下要多读取一行数据；写入数据的时候，实际写入的高度为nRealHeight，Y方向上的偏移量为0。
b、对于介于0和最后一个块之间的块，块的最顶部要和上一块重叠一行像素，块的最下部要和相邻块重叠一行像素，即多读取两行数据，nReadHeight += 2;nYOffset -= 1; 写入数据的时候，实际写入的高度为nRealHeight= nReadHeight - 2;，Y方向上的偏移量为nYOffset = i*nSubHeight;
c、对于最后一个块，块的实际读取数据的高度nReadHeight为nReadHeight += 1，即向上要多读取一行的数据，nReadHeight = nRealHeight + 1;nYOffset -= 1; 实际写入的高度为nRealHeight= nReadHeight - 1;，Y方向上的偏移量为nYOffset = i*nSubHeight;
这样，就保证了分块之间结果缝合在一起了。
讲到了这里，现在就应该讲怎么计算坡度了吧，采用ARCGIS的计算方法，根据公式来计算，代码如下：
最后以90米分辨率的DEM数据作为测试数据，其得到的结果在ARCGIS中分级渲染如下：
这里DEM只有一个波段，所以就不用opencl中图像对象，而是直接采用缓冲区对象，这样所也是为了节约内存以及显存，因为图像对象中每个像素需要存储四个值，所以这里没必要。
opencl的计算函数声明如下：
void SlopeCal_OpenCL(float* poDataIn,float *poDataOut,int nWidth,int nHeight,const SlopeOption* pSlopeType)
函数中poDataIn接收前面分块的输入数据，poDataOut接收分块的输出数据，nWidth是分块的宽度，nHeight是分块数据的高，pSlopeType算法参数结构体。
这里最主要的工作就是需要把poDataIn，nWidth，nHeight，pSlopeType这几个参数传到内核函数中去，至于poDataOut可以不用传输到显存中去，因为是输出参数。poDataIn就必须作为缓冲区对象，缓冲区对象时opencl内核中可用的一块连续的内存区；其他几个参数是普通参数，SlopeOption结构体要传输到内核函数中的话，就必须在.cl文件中声明和主机端一样的结构体。由于结构体中有double型的参数，opencl是默认禁用掉了double类型，所以需要编译器打开，即在cl文件中要声明
#pragma OPENCL EXTENSION cl_khr_fp64: enable
所以算法的内核函数可以声明如下：
__kernel void slope_kernel( __global const float *pSrcData,
__global float *pDestData,const int nWidth,const int nHeight, struct SlopeOption slopeType)
这样，可以用nWidth* nHeight个线程并行地计算各个像素的值，所以主机端设置为一个二维的全局N-D Range空间。
其内核函数的实现如下：
而在主机端，需要将数据拷贝到GPU设备端，以及设置设备端内核函数的参数，其主机端主要代码如下：
12001*12001 23620 5895 4.007
从上表可以看出，其加速比大致维持在4-5之间。不过这个时间是包括了IO时间，如果撇开IO时间，那么统计时间会更短。我觉得这种加速效果不是特别明显，看到有些论文有提到可以提高至少10倍，几十倍，不知道他们是怎么做到的，我觉得程序性能还有提升的空间，还有待挖掘。关于本文的代码已经上传，下载地址为： http://download.csdn.net/detail/zhouxuguang236/7184841
其中opencl和GDAL环境得自己去下载配置了。
2、数字高程模型、李志林、朱庆
3、OpenCL编程指南、苏金国等翻译
又有一段时间没有发表博客了，可能最近工作有点忙。今天就把最近的学习和研究成果和大家分享一下。对于GIS稍微有点了解的人都知道地形分析中的坡度和坡向，这是数字地形分析中最基本的分析了，对于数字地形分析中很多计算都是邻域分析，所以非常适合数据并行。
一、相关概念和公式
坡度严格地讲，是地表任意一点过该点的切平面与水平面之间的夹角。坡度表示了地表的倾斜程度。坡度的计算公式如下：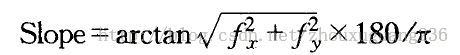
其中fx和fy分别代表x和y方向上的高程变化率。坡度有两种表示方法，一种是坡度角，另外一种是坡度百分比，即高程增量与水平增量的百分比。
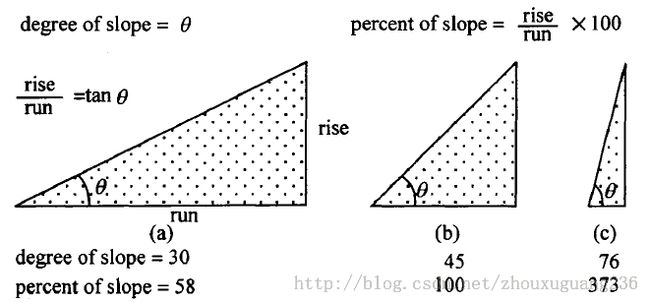
两种表示方法如下：
图：坡度的两种表示方式
而坡向的定义是地面任意一点切平面法线在水平面上的投影与正北方向的方向角。坡向的计算公式如下：
由上面两个公式可以看出，都需要求fx和fy。对于这两个分量的计算方法有很多种。具体的计算方法有二阶差分、三阶差分等，更多的计算方法见下图，图中Slope-we对应fx，Slope-sn对应fy。
各个商业软件基本上都是选取上述的算法进行计算，ArcGIS采用的算法二，ERDAS采用的是算法4。本文采用算法作为计算方法。
二、CPU上的实现
//投影
const char* pszWkt = poSrcDS->GetProjectionRef();
double dbNres = 0;
double dbEres = 0;
double dfGeotrans[6];
if (poSrcDS->GetGeoTransform(dfGeotrans) != CE_None)
{
dbNres = fabs(dfGeotrans[5]);
dbEres = fabs(dfGeotrans[1]);
}
else
{
OGRSpatialReference* pSrs = (OGRSpatialReference*)OSRNewSpatialReference(pszWkt);
if (pSrs != NULL)
{
if (pSrs->IsGeographic())
{
dbNres = fabs(dfGeotrans[5]);
dbNres *= 110000;
dbEres = fabs(dfGeotrans[1]);
dbEres *= 110000;
}
else if (pSrs->IsGeocentric())
{
dbNres = fabs(dfGeotrans[5]);
dbEres = fabs(dfGeotrans[1]);
}
else if (pSrs->IsProjected())
{
dbNres = fabs(dfGeotrans[5]);
dbEres = fabs(dfGeotrans[1]);
}
}
OSRDestroySpatialReference((OGRSpatialReferenceH)pSrs);
}
SlopeOption slopeOption;
slopeOption.dbEwres = dbEres;
slopeOption.dbNsres = dbNres;
slopeOption.slopeType = eSlopeType;
此外，还需要包装两个结构用于传参数；
//坡度的表达方式
typedef enum
{
DEGREE_SLOPE, //度数方式
PERCENT_SLOPE //百分比方式
}SLOPE_TYPE;
//坡度算法结构体
struct SlopeOption
{
double dbNsres; //南北方向分辨率
double dbEwres; //东西方向分辨率
SLOPE_TYPE slopeType; //坡度方式
} ;
最终，我设计的计算坡度的函数如下：
bool ExtractSlope(const char* pszDEMfile,const char* pszOutSlpoeFile,const char* pszFormat, SLOPE_TYPE eSlopeType ,double dbScale)
pszDEMfile为输入DEM数据；pszOutSlpoeFile为输出坡度数据；pszFormat为输出影像格式；
eSlopeType是坡度的类型，即坡度百分比还是坡度角度；dbScale可选，一般情况下为1.0。
在GIS和遥感领域，一般情况下，栅格数据都是非常大的，不可能将所有像素全部读进来一次性处理，所以就必然涉及到影像分块。关于影像分块，对于不同的算法可以采用不同的策略，其主要策略如下：
对于单点运算，即运算过程之和当前计算的像素相关的算法，分块可以按照按照行来分块，也可以矩形分块，类似于地图切片。一般来说，影像是按照行优先的顺序类存储的，所以按照行分块可以减少文件指针移动的次数，提高速度。
对于邻域相关的运算，如本文提到的坡度、卷积等运算，也可以按照行分块或者矩形分块。但是要注意一个问题，这样简单的分块会导致块与块之间的结果不连续。针对这种情况，为了缝合块边缘的结果，可以再读取数据的时候边缘的数据重复读取，这样就保证了最后合成的结果具有连续性，也就是说保证有一定的重叠度，一般重叠度为邻域窗口大小的一半。
还有一种情况是全局相关的运算，如求图像的最值，这个也可以采用上述两种方法都可以，即分好块之后，最后求得各个块的最值。
总结一下，分块的思想体现了算法设计中的分治法思想，即所谓的分而治之。
对于本文，我采用的分块读取、分块处理和分块写入数据的思路如下：
1、按照行来分块，窗口大小为3，所以块之间重叠一个像素；
2、对于分块后只有一个块的情况，不需要做特别处理
3、对于分块后有多个块的情况，也根据块的索引做不同处理：为了说明方便，我先定义几个变量
//实际的块的大小
int nRealWidth = nXsize;
int nRealHeight = nSubHeight;
//读取数据块的大小
int nReadWidth = nXsize;
int nReadHeight = nSubHeight;
int nYOffset = i*nSubHeight; //某一块读取数据的Y方向上的偏移量
nSubHeight为分块的高
a、对于第0个块，块的实际读取数据的高度nReadHeight为nReadHeight += 1;，即向下要多读取一行数据；写入数据的时候，实际写入的高度为nRealHeight，Y方向上的偏移量为0。
b、对于介于0和最后一个块之间的块，块的最顶部要和上一块重叠一行像素，块的最下部要和相邻块重叠一行像素，即多读取两行数据，nReadHeight += 2;nYOffset -= 1; 写入数据的时候，实际写入的高度为nRealHeight= nReadHeight - 2;，Y方向上的偏移量为nYOffset = i*nSubHeight;
c、对于最后一个块，块的实际读取数据的高度nReadHeight为nReadHeight += 1，即向上要多读取一行的数据，nReadHeight = nRealHeight + 1;nYOffset -= 1; 实际写入的高度为nRealHeight= nReadHeight - 1;，Y方向上的偏移量为nYOffset = i*nSubHeight;
这样，就保证了分块之间结果缝合在一起了。
为了方便直观表达其意思，其代码如下：
//分块处理
int nSubHeight = 2000;
int nYBlockCount = (nYsize+nSubHeight-1)/nSubHeight; //计算分块的数量
for (int i = 0; i < nYBlockCount; i ++)
{
//实际的块的大小
int nRealWidth = nXsize;
int nRealHeight = nSubHeight;
//读取数据块的大小
int nReadWidth = nXsize;
int nReadHeight = nSubHeight;
int nYOffset = i*nSubHeight;
if (1 == nYBlockCount)
{
nRealHeight = nYsize;
nReadHeight = nRealHeight;
}
else
{
if (i == 0)
{
nReadHeight += 1;
}
else if (i > 0 && i < nYBlockCount-1)
{
nReadHeight += 2;
nYOffset -= 1;
}
else if(i == nYBlockCount-1)
{
nRealHeight = nYsize-nSubHeight*(nYBlockCount-1);
nReadHeight = nRealHeight + 1;
nYOffset -= 1;
}
}
//读取数据
float* poData = new float[nReadWidth*nReadHeight];
float* poOutData = new float[nReadWidth*nReadHeight];
poBand->RasterIO(GF_Read,0,nYOffset,nReadWidth,nReadHeight,poData,nReadWidth,nReadHeight,GDT_Float32,0,0);
//中间处理过程
//写入数据
int pBandList[] = {1};
if (1 == nYBlockCount)
{
poDstDS->RasterIO(GF_Write,0,nYOffset,nRealWidth,nRealHeight,poOutData,nRealWidth,nRealHeight,
GDT_Float32,1,pBandList,0,0,0);
}
else
{
if (i == 0)
{
poDstDS->RasterIO(GF_Write,0,nYOffset,nRealWidth,nRealHeight,poOutData,nRealWidth,nRealHeight,
GDT_Float32,1,pBandList,0,0,0);
}
else if (i > 0 && i < nYBlockCount-1)
{
poDstDS->RasterIO(GF_Write,0,nYOffset+1,nRealWidth,nRealHeight,poOutData+nRealWidth,nRealWidth,nRealHeight,
GDT_Float32,1,pBandList,0,0,0);
}
else if(i == nYBlockCount-1)
{
poDstDS->RasterIO(GF_Write,0,nYOffset+1,nRealWidth,nRealHeight,poOutData+nRealWidth,nRealWidth,nRealHeight,
GDT_Float32,1,pBandList,0,0,0);
}
}
if (poData != NULL)
{
delete []poData;
poData = NULL;
}
if (poOutData != NULL)
{
delete []poOutData;
poOutData = NULL;
}
}
讲到了这里，现在就应该讲怎么计算坡度了吧，采用ARCGIS的计算方法，根据公式来计算，代码如下：
float SlopeCal (float* afRectData, float fDstNoDataValue,void* pData)
{
const double radiansToDegrees = 180.0 / M_PI;
SlopeOption *psData = (SlopeOption*)pData;
double dx =((afRectData[0] + afRectData[3]*2 + afRectData[6]) -
(afRectData[2]+ afRectData[5]*2 + afRectData[8])) / (psData->dbEwres*8);
double dy =((afRectData[6] + afRectData[7]*2 + afRectData[8]) -
(afRectData[0]+ afRectData[1]*2 + afRectData[2])) / (psData->dbNsres*8);
double key = (dx *dx + dy * dy);
if(psData->slopeType == DEGREE_SLOPE)
{
return (float)(atan(sqrt(key) ) * radiansToDegrees);
//return key;
}
else if (psData->slopeType == PERCENT_SLOPE)
return (float)(100*(sqrt(key) ));
return 0;
}
最后以90米分辨率的DEM数据作为测试数据，其得到的结果在ARCGIS中分级渲染如下：
在arcgis中也基于同样的数据生成坡度数据，发现其边缘像素的值不一样，这是因为边缘处理的策略不一样导致的。
三、基于opencl的GPU实现
这里DEM只有一个波段，所以就不用opencl中图像对象，而是直接采用缓冲区对象，这样所也是为了节约内存以及显存，因为图像对象中每个像素需要存储四个值，所以这里没必要。
opencl的计算函数声明如下：
void SlopeCal_OpenCL(float* poDataIn,float *poDataOut,int nWidth,int nHeight,const SlopeOption* pSlopeType)
函数中poDataIn接收前面分块的输入数据，poDataOut接收分块的输出数据，nWidth是分块的宽度，nHeight是分块数据的高，pSlopeType算法参数结构体。
这里最主要的工作就是需要把poDataIn，nWidth，nHeight，pSlopeType这几个参数传到内核函数中去，至于poDataOut可以不用传输到显存中去，因为是输出参数。poDataIn就必须作为缓冲区对象，缓冲区对象时opencl内核中可用的一块连续的内存区；其他几个参数是普通参数，SlopeOption结构体要传输到内核函数中的话，就必须在.cl文件中声明和主机端一样的结构体。由于结构体中有double型的参数，opencl是默认禁用掉了double类型，所以需要编译器打开，即在cl文件中要声明
#pragma OPENCL EXTENSION cl_khr_fp64: enable
所以算法的内核函数可以声明如下：
__kernel void slope_kernel( __global const float *pSrcData,
__global float *pDestData,const int nWidth,const int nHeight, struct SlopeOption slopeType)
这样，可以用nWidth* nHeight个线程并行地计算各个像素的值，所以主机端设置为一个二维的全局N-D Range空间。
其内核函数的实现如下：
__kernel void slope_kernel( __global const float *pSrcData,
__global float *pDestData,const int nWidth,const int nHeight
, struct SlopeOption slopeType)
{
int j = (int)get_global_id(0);
int i = (int)get_global_id(1);
if (j >= nWidth || i >= nHeight)
return;
int nTopTmp = i-1;
int nBottomTmp = i+1;
int nLeftTep = j-1;
int nRightTmp = j+1;
//处理边界情况
if (0 == i)
{
nTopTmp = i;
}
if (0 == j)
{
nLeftTep = j;
}
if (i == nHeight-1)
{
nBottomTmp = i;
}
if (j == nWidth-1)
{
nRightTmp = j;
}
float dbRectData[9];
dbRectData[0] = pSrcData[nTopTmp*nWidth+nLeftTep];
dbRectData[1] = pSrcData[nTopTmp*nWidth+j];
dbRectData[2] = pSrcData[nTopTmp*nWidth+nRightTmp];
dbRectData[3] = pSrcData[i*nWidth+nLeftTep];
dbRectData[4] = pSrcData[i*nWidth+j];
dbRectData[5] = pSrcData[i*nWidth+nRightTmp];
dbRectData[6] = pSrcData[nBottomTmp*nWidth+nLeftTep];
dbRectData[7] = pSrcData[nBottomTmp*nWidth+j];
dbRectData[8] = pSrcData[nBottomTmp*nWidth+nRightTmp];
double dx = ((dbRectData[0] + dbRectData[3]*2 + dbRectData[6]) -
(dbRectData[2]+ dbRectData[5]*2 + dbRectData[8])) / (slopeType.dbEwres*8);
double dy =((dbRectData[6] + dbRectData[7]*2 + dbRectData[8]) -
(dbRectData[0]+ dbRectData[1]*2 + dbRectData[2])) / (slopeType.dbNsres*8);
double fTmp = (dx *dx + dy * dy);
//计算坡度
double radiansToDegrees = 180.0/M_PI;
double fValue = 0;
if(slopeType.slopeType == DEGREE_SLOPE)
{
fValue = atan(sqrt(fTmp) ) * radiansToDegrees;
}
else if (slopeType.slopeType == PERCENT_SLOPE)
fValue = 100*sqrt(fTmp);
pDestData[i*nWidth+j] = fValue;
}
而在主机端，需要将数据拷贝到GPU设备端，以及设置设备端内核函数的参数，其主机端主要代码如下：
//opencl平台搭建
cl_int status = 0; //状态号码
static cl_context cxGPUContext = NULL; // OpenCL context
static cl_command_queue cqCommandQueue = NULL;// OpenCL command que
static cl_platform_id cpPlatform = NULL; // OpenCL platform
static cl_device_id cdDevice = NULL; // OpenCL device
static cl_program cpProgram = NULL; // OpenCL program
static cl_kernel ckKernel = NULL; // OpenCL kernel
static bool bInit = 0; //是否初始化了
if (!bInit)
{
OpenCLInit(&cpPlatform,&cdDevice,&cxGPUContext);
BuildKernel(cpPlatform,cdDevice,cxGPUContext,&cpProgram,&cqCommandQueue);
ckKernel = clCreateKernel(cpProgram,"slope_kernel",&status);
bInit = 1;
}
cl_int errNum;
cl_mem bufIn = clCreateBuffer(cxGPUContext,CL_MEM_READ_WRITE|CL_MEM_COPY_HOST_PTR,
sizeof(float)*nWidth*nHeight,poDataIn,&errNum);
cl_mem bufOut = clCreateBuffer(cxGPUContext,CL_MEM_WRITE_ONLY,
sizeof(float)*nWidth*nHeight,NULL,&errNum);
//设置参数
status = clSetKernelArg(ckKernel,0,sizeof(cl_mem),&bufIn);
status = clSetKernelArg(ckKernel,1,sizeof(cl_mem),&bufOut);
status = clSetKernelArg(ckKernel,2,sizeof(cl_int),&nWidth);
status = clSetKernelArg(ckKernel,3,sizeof(cl_int),&nHeight);
SlopeOption slopeOpt;
memcpy(&slopeOpt,pSlopeType,sizeof(SlopeOption));
status = clSetKernelArg(ckKernel,4,sizeof(SlopeOption),&slopeOpt);
//执行核函数
size_t globalThreads[] = {nWidth,nHeight};
status = clEnqueueNDRangeKernel(cqCommandQueue,ckKernel,2,
NULL,globalThreads,NULL,0,NULL,NULL);
status = clFinish(cqCommandQueue);
status = clEnqueueReadBuffer(cqCommandQueue,bufOut,CL_TRUE,0,sizeof(float)*nWidth*nHeight,poDataOut,0,NULL,NULL);
当然，最后也别忘了释放之前在GPU设备上申请的内存。
四、性能测试
通过对几组数据进行测试，分别用一副90米分辨率、宽和高为6001的DEM数据以及12001*12001的数据进行测试。测试环境为N卡GT750M。分别对这两组不同数据进行大量测试，并且取得其平均值，其测试结果见下表。数据 CPU时间（毫秒） GPU时间（毫秒） 加速比
6001*6001 5846 1385 4.22112001*12001 23620 5895 4.007
从上表可以看出，其加速比大致维持在4-5之间。不过这个时间是包括了IO时间，如果撇开IO时间，那么统计时间会更短。我觉得这种加速效果不是特别明显，看到有些论文有提到可以提高至少10倍，几十倍，不知道他们是怎么做到的，我觉得程序性能还有提升的空间，还有待挖掘。关于本文的代码已经上传，下载地址为： http://download.csdn.net/detail/zhouxuguang236/7184841
其中opencl和GDAL环境得自己去下载配置了。
参考文献
1、地理信息系统算法基础、张宏等2、数字高程模型、李志林、朱庆
3、OpenCL编程指南、苏金国等翻译