【贪心】【POJ3154】墓地雕塑(Graveyard, NEERC 2006, LA 3708)需要稍稍加工的(先贪心,再确保能这样贪(可行性&&如果可行必定最优&&非证明最优性)的题)(K)
例题4 墓地雕塑(Graveyard, NEERC 2006, LA 3708)
在一个周长为10000的圆上等距分布着n个雕塑。现在又有m个新雕塑加入(位置可以随意放),希望所有n+m个雕塑在圆周上均匀分布。这就需要移动其中一些原有的雕塑。要求n个雕塑移动的总距离尽量小。
【输入格式】
输入包含若干组数据。每组数据仅一行,包含两个整数n和m(2≤n≤1 000,1≤m ≤1 000),即原始的雕塑数量和新加的雕塑数量。输入结束标志为文件结束符(EOF)。
【输出格式】
输入仅一行,为最小总距离,精确到10-4。
【样例输入】
2 1
2 3
3 1
10 10
【样例输出】
1666.6667
1000.0
1666.6667
0.0
这道题 是一边写博客 一边思考的一道题
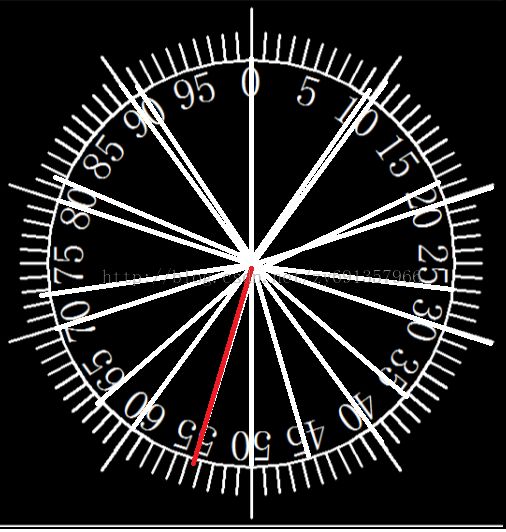
首先 显然发现 +了雕像后 可以保证一个雕像始终不会动
这是 10个雕像 变为11个雕像的时候 显然发现因为11个雕像的时候间距小于10个雕像的时候
使得在(11)红线 前面的(10)白线 选择移动到前方更近
在(11)红线 后方的(10)白线 选择移动到后方更近
显然
在m=1的情况下 选择附近最近的搬移位置即可 且能保证不会有2个雕像搬到同一位置
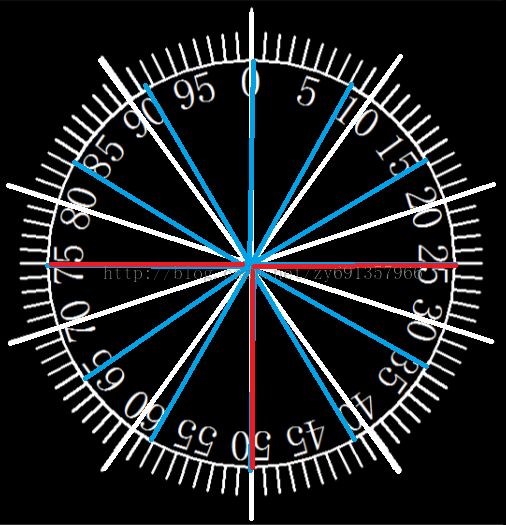
考虑m=2 :
10个雕像 变为12个雕像的时候
3个红色的线就是几条类似上面11时候红色的 分界线
我们可以也发现。。 搬移到附近最近位置即可;
。。。但是只能从图片上看出
严格证明想了一段时间还是没有想出来
好吧 似乎通过严格证明再得出 搬到附近最近的位置这个结论估计是不行的。
只能通过 搬到附近最近的位置这个假设 证明出是最优解 并且证明出不会搬移到同一点(书上解法)
书上面有讲解 不过因为是直接看书得出的题解 我还是过两天自己仿书上写一遍题解吧 (今天10-10)
10-12 再次编辑:
step1:
为了使操作简便 假设长度为N+M(后面知道这一步是这道题的精髓)
step2:
原雕塑位置为pos=((N+M)/N )*i (i=0...N-1)
step3:
根据我们上面的图的操作我们知道要找距离最近的点
(若不搬到同一处 显然是最优的,但不知道是否正确)
那么该如何找最近的点呢?
这就体现了step 1的优越性了
floor(pos+0.5) 即可
四舍五入即为一个寻找最近的整数点的方法不是吗?
新雕塑的位置全部为一个整数点;
所以是一个十分赞的方法
程序流程到此结束
证明:
为何这样是正确的?证明可行性
反证法:
假设有两个原雕塑搬到同一点 比如 2
那么 两个雕塑相距最远的可能是什么?
1.49999999999 与 2.49999999999
即使这样两者距离也不过是等于1
显然可知原雕塑距离一定要大于1的
固不可能搬到同一点(这也是当时缩放的一个好处,便于推理)
小贴士:
如果考试的时候无法证明这一点怎么办?
不如从1 for 到 10000 打表证明不存在这种情况
打表程序如下:
AC代码如下:
#include<cstdio>
#include<cmath>
using namespace std;
int main()
{
int n,m;
double pos,ans;
while(scanf("%d%d",&n,&m)!=EOF)
{
ans=0;
for(int i=0;i<n;i++)
{
pos=(double)(n+m)/n*i;
ans=ans+abs(floor(pos+0.5)-pos);
}
printf("%.4lf\n",ans*10000/(double)(n+m));
}
return 0;
}